¿Qué son las firmas digitales y cómo funcionan?

Las firmas digitales son como versiones electrónicas de sus firmas manuscritas. Permiten a las personas verificar el autenticidad e integridad de los datos, además de evitar que el firmante pueda repudiar (negar) su participación.

Estas propiedades han llevado a la adopción de firmas digitales en una amplia gama de aplicaciones, incluidos muchos de nuestros protocolos de seguridad, correo electrónico seguro y gestión de derechos digitales..

En este artículo, discutiremos que son las firmas digitales, dónde se usan, así como los detalles técnicos de dos de los algoritmos más populares, RSA y DSA.

¿Qué son las firmas digitales??

Como se indicó anteriormente, las firmas digitales nos proporcionan tres propiedades muy importantes. Estos son autenticación, integridad y no repudio.

Autenticación es el proceso de verificar que la persona que envía un mensaje es realmente quien dice ser y no un impostor.

los integridad de datos o un mensaje se refiere a si ha llegado en el mismo estado en que se envió. Si un mensaje ha sido alterado o alterado, ya no conserva su integridad..

Si hay datos o un mensaje no repudiable, significa que su autor no puede disputar que ellos fueron los verdaderos creadores del documento. Esta propiedad elimina la negación plausible, o la antigua excusa “Lo siento, mi amigo estaba usando mi cuenta”.

Mientras la clave privada del individuo no se haya visto comprometida, las firmas digitales pueden proporcionar estas tres propiedades a los datos.

Quizás se esté preguntando por qué necesitamos estas propiedades en primer lugar. Retrocedamos y pensemos en cómo hacemos las cosas en un encuentro cara a cara..

Digamos que le debes $ 100 a tu amigo Mike. Eres una buena persona, así que estás feliz de devolverle el dinero cuando recibas el dinero.

La mejor manera de hacerlo sería darle un billete de $ 100 a Mike. Lo conoces desde hace años y sabes cómo es, así que sería Es fácil verificar su identidad y así autenticar que le está dando el dinero a la persona adecuada..

Si fueras realmente anal, incluso podrías verificar su identificación y hacer que firme un recibo escrito a mano por ti. La firma en el recibo le daría integridad y lo haría no repudiable.

¿Qué pasa si en lugar de hacer la transacción cara a cara, recibes una llamada de alguien que dice que son Mike y que debes enviar $ 100 al número de cuenta 12345678?.

“Pero no suenas como Mike”, dices.

“Tengo un resfrío. Envíalo ahora, necesito el dinero.

¿Enviarías el dinero? Probablemente no.

No hay forma de saber si realmente es Mike o el número de cuenta correcto. Por lo que sabes, podría ser un impostor que intente robarte. En lugar de transferir el dinero de inmediato, sería mejor esperar hasta que veas a Mike para poder darle el efectivo en persona..

Al igual que en el escenario anterior, con frecuencia nos encontramos con situaciones en las que necesitamos verificar la identidad de una parte o la integridad de los datos en el mundo en línea. Es por eso que las firmas digitales han surgido como un mecanismo que puede proporcionar estas propiedades y facilitar transacciones seguras en línea..

Sin ellos, es posible que no sepamos con quién estamos hablando, no podríamos estar seguros de si los datos han sido alterados o no, y la persona podría negar que fueron responsables.

Los usos de las firmas digitales

Estas propiedades de las firmas digitales las hacen útiles en una amplia variedad de aplicaciones. A menudo se usan solos o junto con el cifrado en una variedad de protocolos de seguridad diferentes, como:

• IPsec
• SSH
• TLS

También se usan con frecuencia en gestión de derechos digitales, en tecnología blockchain, en gestión de contratos aplicaciones, como parte de distribución de software, y en Finanzas.

Historia de las firmas digitales.

La idea de las firmas digitales fue planteada por primera vez por los reconocidos criptógrafos Whitfield Diffie y Martin Hellman en su artículo de 1976. Nuevas direcciones en criptografía. En 1978, Ronald Rivest, Adi Shamir y Len Adleman presentaron el algoritmo RSA a la vista del público, que podría utilizarse para producir firmas digitales inseguras..

Las firmas digitales tardaron otra década en aparecer en una aplicación generalizada: el lanzamiento de Lotus Notes 1.0 de IBM. A partir de ese momento, las firmas digitales comenzaron a ver una adopción más amplia a medida que surgieron nuevas técnicas y creció la necesidad de autenticación en línea y verificaciones de integridad..

Una breve introducción a la criptografía de clave pública

Antes de saltar a las firmas digitales, es mejor cubrir algunos de los aspectos importantes de la criptografía de clave pública, que forman la base de cómo funcionan las firmas digitales.

Si es relativamente nuevo en criptografía, el sistema con el que estará más familiarizado es el cifrado de clave simétrica. Esto solo significa que la misma clave (que es similar a una contraseña, pero tiene algunas diferencias) se usa para cifrar y descifrar datos.

El cifrado de clave pública fue una revolución, porque implicó utilizando claves separadas para el proceso de cifrado y descifrado, lo que lleva a una gama de diferentes aplicaciones criptográficas. Estas dos claves formaron un par de claves, compuesto por la clave pública y la clave privada. La clave pública obviamente se puede compartir públicamente, mientras que la clave privada debe mantenerse en secreto para que el sistema sea seguro.

Los dos usos más comunes de la criptografía de clave pública son el cifrado y las firmas digitales..

Cifrado

Una de las características innovadoras de la criptografía de clave pública fue que permite que las partes que nunca se hayan reunido se envíen mensajes de forma confidencial. El remitente busca la clave pública del destinatario deseado (se puede encontrar en servidores de clave pública, en sitios web personales o simplemente preguntando a la persona), luego encripta un mensaje con esta clave, antes de enviarla al destinatario.

El destinatario es la única persona que puede acceder al mensaje, suponiendo que la clave privada no haya sido comprometida, descifrándola con su clave privada. Aunque la clave pública se usó para cifrar el mensaje, solo puede ser descifrada por la clave privada. Si el destinatario desea responder, encuentra la clave pública del remitente original y luego repite el proceso..

Consulte también: Tipos de cifrado comunes explicados

¿Cómo funcionan las firmas digitales??

Como hemos dicho, las firmas digitales se utilizan para la autenticación, para ver si los datos han sido alterados y para proporcionar no repudio. Hay una variedad de mecanismos diferentes que se pueden usar para las firmas digitales, y cada uno tiene ligeras variaciones en cómo están estructurados..

En general, estos algoritmos deben estar compuestos por tres sub-algoritmos:

• Un algoritmo de generación de claves. – Este algoritmo genera un par de claves aleatorias para un usuario. Los números involucrados en el par de claves deben cumplir con ciertos parámetros para ser considerados seguros. Dos de los aspectos más importantes son que los números son suficientemente aleatorios y de tamaño adecuado..
• Un algoritmo para firmar datos – Una vez que un usuario tiene sus claves, hay formas específicas de cómo se aplican a los datos en el proceso de firma.
• Un algoritmo para verificar la firma. – Del mismo modo, la verificación de una firma sigue un proceso predeterminado.

Para que un sistema de firma digital sea efectivo, debe estructurarse de tal manera que:

• Los datos firmados con una clave privada son verificado con la clave pública coincidente del mismo individuo.
• Debería ser esencialmente imposible (utilizando la tecnología y las técnicas actuales) falsificar una firma válida sin conocer la clave privada del individuo.

Algunos de los esquemas de firma digital más comunes incluyen RSA, DSA, EcDSA y EdDSA.

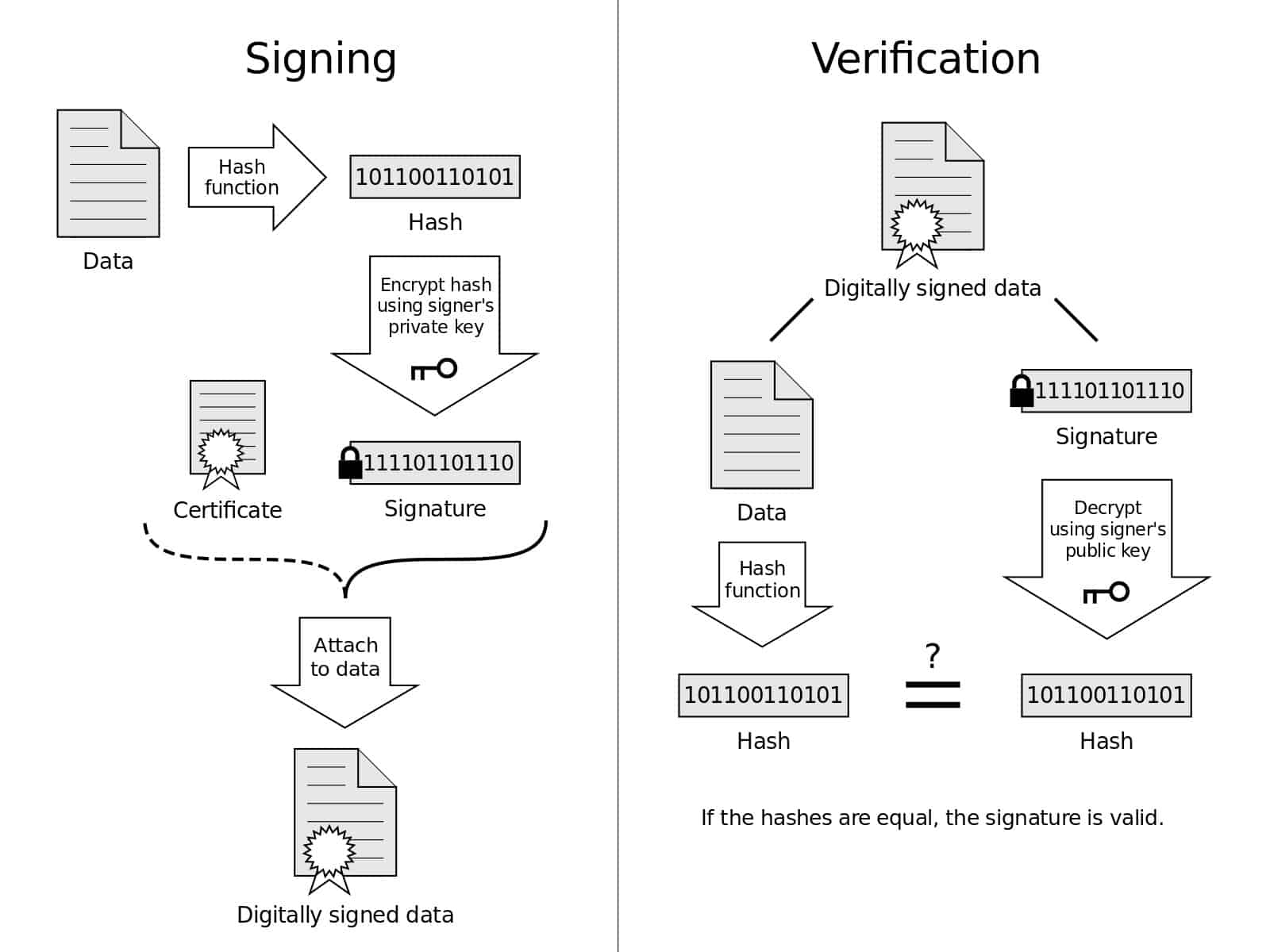
Esta imagen ofrece una representación visual de los procesos de firma y verificación.. Diagrama de firma digital por Acdx con licencia bajo CC0

RSA

RSA fue el primer algoritmo de firma digital, pero también se puede usar para el cifrado de clave pública. En este artículo, omitiremos el aspecto del cifrado, pero puede obtener más información al respecto en nuestro artículo completo que cubre qué es RSA y cómo funciona.

Generación de clave RSA

En implementaciones seguras de RSA, los pares de claves generalmente se establecerán automáticamente bajo el siguiente proceso:

Primera generación

Se seleccionan dos números primos individuales, pag y q. El tamaño exacto de estos números primos variará según el tamaño de la clave. En estos días, se recomienda un mínimo de claves RSA de 2048 bits para una seguridad adecuada, por lo que estamos hablando de dos números primos que se multiplican para producir un número de 2048 bits..

2048 bits es un tamaño en el sistema de números binarios. Si un número de este tamaño se convirtiera a nuestro sistema decimal más familiar, sería aproximadamente así de largo:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Los primos en RSA deben seleccionarse al azar y deben tener longitudes similares.

En nuestro ejemplo, utilizaremos números mucho más pequeños para que las cosas sean más fáciles de entender. Tenga en cuenta que el uso de claves de este tamaño haría que las firmas digitales sean triviales a falsas. Es por eso que en la práctica se usan valores tan grandes.

Digamos que:

pag = 13

q = 17

El primer paso sería calcular el módulo norte usando la siguiente fórmula:

n = pq

norte = 13 x 17

norte = 221

El valor de norte también es la longitud de la clave.

La función totient de Carmichael

Ahora que tenemos el valor para norte, El siguiente paso es utilizar la función totient de Carmichael:

λ(norte) = mcm (pag – 1, q – 1)

Hay algunas cosas que debes entender:

• λ(norte) significa el paciente de Carmichael por el valor de norte
• mcm representa el multiplicador común más bajo. Este es el número común más bajo que ambos p-1 y q-1 puede dividirse en

Pongamos nuestras cifras en la ecuación:

λ(221) = mcm (13 – 1, 17 – 1)

λ(221) = mcm (12, 16)

Si eres bueno en matemática mental, es posible que hayas descubierto que 48 es el multiplicador común más bajo de ambos 12 y dieciséis. Esto se debe a que 48 es el número más pequeño en el que caben ambos números (12 x 4 = 48, 16 x 3 = 48). Por lo tanto:

λ(221) = 48

Subiendo con la clave pública

En RSA, la clave pública se compone del valor norte (que ya hemos calculado como 221) y mi. Dado que la clave pública se comparte libremente, el valor de mi no tiene que ser un secreto De hecho, a menudo se establece en 65.537 en la práctica, porque un número mayor ralentizaría el proceso de cifrado. En nuestro ejemplo, estableceremos mi a 5, solo para que sea un número pequeño y simple para trabajar.

Por lo tanto, la clave pública para este ejemplo se compone de 221 y 5 5. Cubriremos los detalles de cómo se aplica la clave pública en las siguientes secciones.

Averiguar la clave privada

Así como nuestra clave pública se compone de dos números, también lo es nuestra clave privada. Las claves privadas se componen de re y mi. Ya sabemos el valor de mi (5), y podemos usar la siguiente fórmula para encontrar re:

re = 1 /mi modificación λ(norte)

Tenga en cuenta que modificación simplemente simboliza una operación de módulo, lo que normalmente significaría que debe encontrar el resto una vez que divida el lado izquierdo por el derecho. Como ejemplo:

17 mod 3 = 2

Esto se debe a que 3 encaja en 17 un total de 5 veces, con un resto de 2.

Nuestro ejemplo es un poco diferente. Los “1 /mi modificación“Puede parecer que el segmento de la ecuación te está diciendo que dividas 1 por mi, pero en realidad no lo es. Es confuso, pero esta es una forma de representar el inversa modular. La ecuación en realidad nos dice que calculemos el inverso modular de mi y λ(norte).

El inverso modular normalmente se deriva utilizando el algoritmo euclidiano extendido, pero no lo trataremos en este artículo. En cambio, solo usaremos una calculadora en línea para facilitar las cosas.

Ahora que lo hemos logrado, ingresemos nuestros valores en la fórmula:

re = 1/5 mod 48

Encontrar re, todo lo que tenemos que hacer es ingresar nuestro valor para mi (5) en la calculadora en línea donde dice entero, entonces nuestro valor para λ(norte), cual es 48, En donde dice módulo.

Esto nos da un resultado de 29 De acuerdo con la calculadora en línea. Por lo tanto, nuestra clave privada estará compuesta por:

mi = 5 5

re = 29.

Ahora que hemos generado nuestras dos claves, la siguiente pregunta es: “¿Qué hacemos con ellas?” Bueno, podríamos usarlas para cifrar y descifrar mensajes mediante criptografía de clave pública, pero este artículo trata sobre firmas digitales, así que nos centraremos en eso.

Firma digital de datos con RSA

Digamos que alguien quiere enviar un mensaje a su amigo, pero quiere asegurarse de que el amigo pueda verificar la autenticidad e integridad del mensaje. Podrían hacerlo utilizando una firma digital RSA para firmar el mensaje..

El primer paso es ejecutar todo el mensaje a través de una función hash. Estas son funciones unidireccionales que siempre ofrecen la misma salida para una entrada determinada. Las funciones de hash seguro son esencialmente imposibles de revertir, lo que significa que la salida no se puede usar para calcular la entrada. También es inviable que dos mensajes separados tengan la misma salida.

Puede encontrar más información sobre las funciones hash en el ¿Qué es el hashing?? Seccion de nuestro articulo, Cifrado, hash, salazón: ¿cuál es la diferencia??

Digamos que queremos firmar digitalmente el mensaje “Hace calor hoy“Para que nuestro destinatario pueda saber si el mensaje es auténtico o no y si ha sido manipulado. Entonces correríamos “Hace calor hoy“A través de una función hash.

Comprender las funciones hash

En estos días, la función hash segura más utilizada es SHA-256. Cuando enviamos nuestro mensaje a través de una calculadora SHA-256 en línea, nos da un resultado como este:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Esto plantea algunos problemas para nuestro ejemplo. La primera es que no es un número decimal como los que la mayoría de la gente está acostumbrada. Es posible que haya notado que hay letras en este número, y que solo van hasta F. Esto nos da una pista de que en realidad es un número hexadecimal.

los El sistema hexadecimal se basa en una base de 16, en lugar de una base de 10, como el sistema de números que usamos normalmente. Esto significa que, en lugar de contar en múltiplos de 10, cuenta en múltiplos de 16, y las primeras 6 letras de nuestro alfabeto se utilizan para formar estos números adicionales. Un número como este se puede convertir a nuestro sistema decimal diario, pero eso está fuera del alcance de este artículo.

El segundo problema que tenemos es que este es un número realmente grande. Si se convirtiera a decimal, sería aún más largo. Dado que buscamos simplicidad en esta guía, ejecutar los cálculos con un número tan grande haría que las cosas fueran demasiado confusas para transmitir los conceptos básicos.

Con la idea de demostrar cómo funcionan las firmas digitales RSA de una manera fácil de entender, no utilizaremos un valor hash tan grande en el siguiente ejemplo. En su lugar, pretendemos que el valor hash de “Hace calor hoy” es simple 10.

También tendremos que fingir que, como cualquier hash real, cada vez que ponemos nuestra entrada de “Hace calor hoy” a través de la función hash, siempre devolverá el valor de 10. Para ser coherentes con el funcionamiento normal de las funciones hash, tendremos que fingir que es increíblemente improbable que cualquier otra entrada dé el mismo valor. Del mismo modo, tenemos que fingir que tampoco es factible determinar nuestra entrada original a partir de este valor. Estas propiedades son las que hacen que los hashes sean inmensamente útiles.

Cómo se usa la clave privada del remitente para firmar digitalmente el valor hash

Nuestro remitente ha escrito su mensaje, luego lo ha sometido a una función hash, que pretendemos que devuelve un valor de 10. Una vez que el remitente tiene el hash del mensaje, puede crear la firma digital aplicando su clave privada al valor hash con la siguiente fórmula:

metro (C) = Cre modificación norte

Esta es en realidad la fórmula para descifrar datos que se han cifrado con la clave pública del destinatario, pero también se utiliza para firmar documentos digitalmente.

Cuando se trata de firmas digitales:

• El valor de metro (C) será la firma.
• El valor de C es el hash del mensaje (10).
• El valor de re es parte de la clave privada del remitente, que derivamos anteriormente (29).
• los modificación la función es la misma operación restante que cubrimos anteriormente.
• El valor de norte es la otra parte de la clave privada del remitente, que calculamos al inicio (221).

Entonces, pongámoslo todo en nuestra fórmula:

metro (C) = 1029 mod 221

    metro (C) = 100,000,000,000,000,000,000,000,000,000 mod 221

Pasemos esto a través de la siguiente calculadora de módulo (explicamos cómo funcionan estas operaciones bajo el Descubrir la clave pública sección). Para que funcione correctamente, necesitamos configurar nuestras entradas como:

• Número un tipo – decimal
• Número un valor – 100000000000000000000000000000
• Número si tipo – decimal
• Número si valor – 221
• Ecuación de cálculo (este es solo el código que le dice a la calculadora qué operación realizar. Este y otros códigos se pueden encontrar en la página web vinculada arriba de la sección de entrada) – mod (a, b)

Si ha hecho las cosas correctamente, debería verse así:

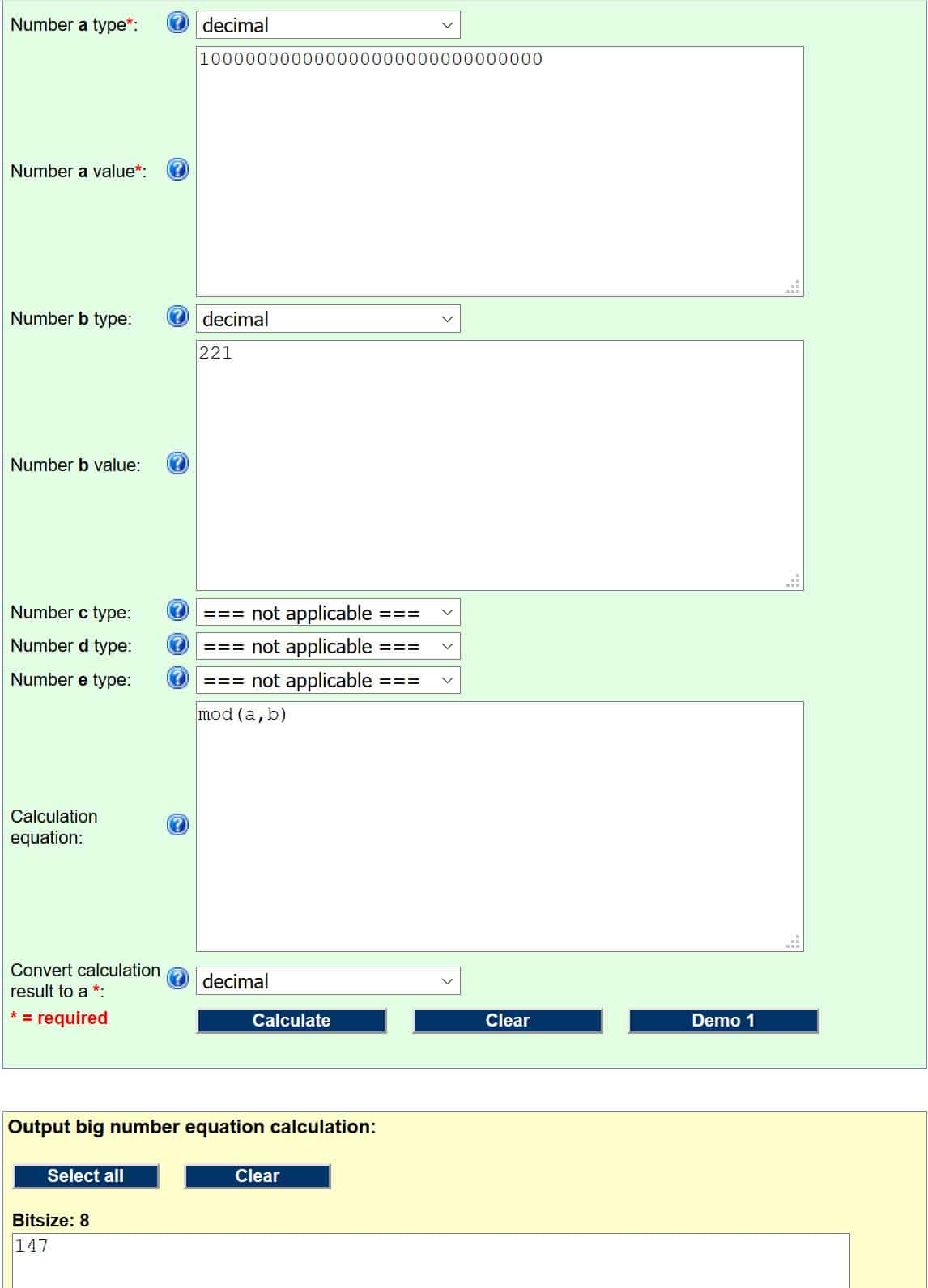
El número en el cuadro amarillo es nuestra respuesta, por lo que la firma digital para el hash del mensaje es 147.

Para demostrar la autenticidad e integridad del mensaje, junto con proporcionar no repudio, nuestro remitente transmitirá el mensaje “Hace calor hoy“Junto con la firma digital de 147 a su destinatario deseado. Solo recuerde que usamos un valor pequeño para el hash para simplificar las cosas, en lugar del hash real del mensaje.

Verificación de firmas digitales

Las firmas digitales solo son útiles si podemos verificar si son legítimas. Mientras la clave privada de un remitente no se haya visto comprometida, el destinatario puede probar si un mensaje es auténtico y conserva su integridad aplicando la siguiente fórmula a la firma digital:

    cm) = metromi modificación norte

En una inversión del proceso de firma, esta es en realidad la fórmula que se utiliza para cifrar datos en RSA. Cuando usamos esta fórmula para verificar las firmas:

• El valor de cm) será el valor de hash del remitente en el momento en que lo firmó (debido a la estructura del algoritmo de clave pública RSA, la aplicación de la clave pública del remitente a través de esta fórmula deshacerá la operación de firma que acabamos de realizar, dejándonos con nuestro hash de simulación original ).
• El valor de metro es la firma digital (147).
• El valor de mi es parte de la clave pública del remitente, que derivamos anteriormente (5 5).
• los modificación la función es la misma operación restante que cubrimos anteriormente.
• El valor de norte es la otra parte de la clave pública del remitente, que calculamos al inicio (221).

Vamos a incluirlo todo en la fórmula:

    cm) = 1475 mod 221

    cm) = 68,641,485,507 mod 221

Usemos la misma calculadora de módulo que antes y mantengamos todo igual, excepto:

• Número un valor – 68,641,485,507

Si ha ingresado las cosas correctamente, debería obtener un resultado de:

cm) = 10

Ahora que el destinatario ha calculado el valor hash de la firma digital, su próximo paso es calcular el valor hash del mensaje que recibió, “Hace calor hoy“. Si recuerdas de antes, en realidad no utilizamos el hash SHA-256 real del mensaje, porque el número habría sido demasiado grande y el ejemplo demasiado complicado..

En cambio, hemos estado pretendiendo que la función hash realmente nos dio el pequeño número, 10, para nuestro aporte. Dado que las funciones hash siempre generan el mismo resultado para una entrada dada, cuando nuestro destinatario pone “Hace calor hoy“A través de nuestra función hash imaginaria, también habrían recibido el valor de 10.

El proceso de verificación de firma da como resultado dos valores. El primer valor es el hash tal como era cuando el remitente lo firmó digitalmente con su clave privada. Calculamos esto arriba usando la clave pública del remitente.

El segundo valor es el hash del mensaje que recibió el destinatario. Esto se calcula usando la misma función de hash que el remitente usó para hash su mensaje original. Estos dos valores se comparan y, si los valores son iguales, podemos suponer que el mensaje es auténtico, conserva su integridad y que no es repudiable. Por supuesto, esto supone que la clave privada del remitente no ha sido comprometida.

Como nuestro ejemplo devolvió un valor de 10 para el hash cuando fue firmado por el remitente, así como un valor de 10 como el hash del mensaje recibido, podemos suponer que el mensaje “Hace calor hoy” proviene de la persona que dice haberlo enviado, y que no ha sido alterado desde que fue enviado.

Si el destinatario desea responder para que su corresponsal pueda verificar su mensaje de la misma manera, se repite todo el proceso, excepto que las claves privadas y públicas del destinatario se utilizan para los procesos de firma y verificación, respectivamente..

Es posible que todas estas matemáticas te hayan quitado la idea de las firmas digitales. No se preocupe, porque las implementaciones de RSA automatizan este proceso, por lo que no tiene que anular ningún número.

Profesionales de RSA & contras

RSA es uno de los algoritmos de firma digital más ampliamente soportados e implementados, aunque hay un movimiento hacia los algoritmos más nuevos, más eficientes y seguros como ECDSA y EdDSA.

En comparación con DSA (que veremos en la siguiente sección), RSA es más rápido para verificar las firmas, pero más lento para generarlas. Dado que las firmas tienden a crearse una vez y verificarse muchas veces, generalmente se prefiere RSA sobre DSA.

DSA

La seguridad del algoritmo de firma digital se basa en dos conceptos matemáticos, el problema del logaritmo discreto y algunas propiedades de la exponenciación modular. Para algunos grupos, no es factible calcular sus logaritmos discretos con las técnicas y la tecnología actuales..

Generación de claves DSA

Para generar claves DSA, el primer paso es elegir los parámetros que un grupo de usuarios en el mismo sistema puede usar para generar un par de claves.

Generando los parámetros

• Elegir un función hash – SHA-256 es la opción más común para cumplir con los requisitos de seguridad modernos.
• Estableciendo longitudes de tecla, L y norte – Estos días, L debe tener al menos 2.048 bits de largo, mientras que norte debe tener al menos 256 bits.
• Decide una prima, q, esa es la misma longitud que norte.
• Seleccione una prima, pag, dónde pag-1 es un múltiplo de q.
• Elige un número, sol, usando la siguiente fórmula (donde h es un número arbitrario entre 1 y p-1):

sol = h(pag – 1) /q modificación pag

Normalmente, estos valores son números muy grandes para que el algoritmo sea seguro. Para evitar que nuestro ejemplo sea demasiado difícil de calcular o explicar, utilizaremos números mucho más pequeños que en realidad no serían seguros. Digamos que:

    q = 5

    pag = 11

Encontrar sol, conectamos nuestros números a la fórmula. Usaremos 3 como nuestro valor para h:

sol = 3 (11-1) / 5 mod 11

sol = 32 mod 11

sol = 9 mod 11

Usaremos la misma calculadora de módulo que en Cómo se usa la clave privada del remitente para firmar digitalmente el valor hash sección. Los parámetros serán los mismos, excepto:

• Número un valor – 9 9
• Número si valor – 11

Si ha ingresado todo correctamente, le dará un resultado para sol de 9 9.

Generando las claves de usuario

Los usuarios individuales toman estos parámetros y los usan para formar su par de claves:

• La clave privada (X) es un número intermedio 0 y q, que establecemos en 5. Para nuestro ejemplo, elegiremos 2 para ser X, nuestra clave privada.
• La clave pública (y) se calcula utilizando la siguiente fórmula:

    y = solX modificación pag

Por lo tanto:

y = 92 mod 11

y = 81 mod 11

Usaremos la misma calculadora de módulo una vez más. Los parámetros serán los mismos, excepto:

• Número un valor – 81
• Número si valor – 11

Si ha ingresado las cosas correctamente, debería haber obtenido un resultado de y = 4. La clave pública es por lo tanto 4 4.

Ahora que hemos generado todos nuestros valores, le ofreceremos un resumen rápido. Los parámetros para el sistema son:

• pag = 11
• q = 5
• sol = 9

Nuestro par de llaves está compuesto por:

• La clave privada, X = 2
• La clave publica, y = 4

Firma digital de datos con DSA

Los remitentes pueden usar su clave privada DSA para firmar digitalmente datos, lo que permite a su destinatario verificar si el mensaje es auténtico y conserva su integridad. También evita que el remitente pueda repudiar el mensaje.

El proceso de firma comienza generando un valor aleatorio k, que está entre 1 y q. Para este ejemplo, simplemente elijamos 3 como nuestro número “aleatorio”, k.

Luego seguimos la siguiente fórmula para crear una clave individual (r) para el mensaje:

r = (solk modificación pag) mod q

Agreguemos nuestros números:

r = (93 mod 11) mod 5

r = (729 mod 11) mod 5

Usamos nuestra calculadora de módulo nuevamente, ingresando 729 y 11, lo que nos da un resultado de 3. Por lo tanto:

r = 3 mod 5

Y luego repetimos la operación de módulo nuevamente con los nuevos valores para darnos:

r = 3

Nuestro valor para r se usa como clave para el mensaje.

Se nos ocurre la otra parte de la firma digital., s, con la siguiente fórmula:

s = k-1(H(metro) + xr) modificación q

los k-1 no representa tomar el poder negativo de k, sino que calcula el inverso modular, como en nuestro Averiguar la subsección de clave privada en la parte anterior del artículo donde hablamos sobre RSA.

H(metro) es el valor hash para el mensaje que está firmando el remitente. Normalmente, este sería un valor hash largo derivado del mensaje, al igual que en el Comprender los valores hash subsección anterior, que cubrimos cuando estábamos hablando del algoritmo RSA.

Para este ejemplo, mantendremos las cosas simples. Al igual que en la sección RSA, diremos que nuestro mensaje, metro, es “Hace calor hoy“ y que el hash del mensaje H(metro), es 10.

Así que ingresemos todos nuestros valores en la fórmula:

s = 3-1 (10 + 2 x 3) (mod 5)

s = 3-1 (10 + 6) (mod 5)

s = 3-1 (16) (mod 5)

Ahora, tomamos el inverso modular de 3 por el orden de 5 5 (porque 5 5 es nuestro valor para q), usando la misma calculadora inversa modular de antes. Entrar 3 como el entero y 5 5 como el módulo, que le dará un resultado de 2. Por lo tanto:

s = 2 (16) (mod 5)

s = 32 (mod 5)

Volvamos a nuestra calculadora para la operación de módulo normal, manteniendo los mismos parámetros que usamos anteriormente, excepto:

• Número un valor – 32
• Número si valor – 5 5

Si ha hecho esto correctamente, dará un valor para s de 2. La firma digital se compone de r y s (3 y 2, respectivamente). Los remitentes transmiten la firma digital a su destinatario junto con su mensaje “Hace calor hoy“. También compartirán los valores de p, q, sol y y con su destinatario.

Verificación de firmas digitales

Cuando el destinatario recibe la firma digital junto con el mensaje, puede verificar la integridad y autenticidad del mensaje con el siguiente conjunto de cálculos.

El primer paso es encontrar el hash del mensaje que recibieron. El destinatario hace esto ejecutando todo el mensaje a través de una función hash. Para mantener las cosas simples y consistentes, digamos que el hash del mensaje, H(metro) es 10.

Al destinatario también se le han enviado los siguientes valores, que utilizan en el proceso de verificación:

• La firma digital (r, s) – 3, 2
• p – 1
• q – 5
• g – 9
• y – 4

El primer cálculo es encontrar w:

w = s-1 mod q

De nuevo, el s-1 representa tomar el inverso modular. Ingresemos nuestros valores:

w = 2-1 mod 5

Usaremos la calculadora inversa modular de antes. Entrar 2 como el entero y 5 5 como el módulo, que le dará un resultado de 3 para w. El siguiente paso es encontrar tu1 con la siguiente fórmula:

tu1 = H(metro) X w modificación q

Agreguemos nuestros valores:

tu1 = 10 x 3 mod 5

tu1 = 30 mod 5

Volviendo a la calculadora de módulo normal, manteniendo los mismos parámetros que utilizamos anteriormente, excepto:

• Número un valor – 30
• Número si valor – 5 5

Esto nos da un resultado de 0 para tu1.

Usamos la siguiente fórmula para llegar a tu2:

tu2 = r X w modificación q

Ingresemos nuestros números:

tu2 = 3 x 3 mod 5

tu2 = 9 mod 5

Luego volvemos a la calculadora de módulo normal, usando los mismos parámetros que antes, excepto:

• Número un valor – 9 9
• Número si valor – 5 5

Si ingresa esto correctamente, le dará un resultado para tu2 de 4.

Ahora que tenemos nuestros valores para tu1 y tu2, podemos encontrar v, con la siguiente fórmula:

v = (solu1yu2 modificación pag) modificación q

Agreguemos nuestros números:

v = (90 x 44 mod 11) mod 5

v = (1 x 256 mod 11) mod 5

v = (256 mod 11) mod 5

Volvemos a nuestra calculadora de módulo normal, usando los mismos parámetros que antes, excepto:

• Número un valor – 256
• Número si valor – 11

Esto nos da un resultado de 3. Por lo tanto:

v = 3 mod 5

Luego usamos la calculadora de módulo normal una última vez, nuevamente con los mismos parámetros, excepto:

• Número un valor – 256
• Número si valor – 11

Esto nos da un resultado para v de 3.

Si el mensaje es auténtico y no ha sido manipulado, entonces v será igual a r:

    v = 3

    r = 3

    3 = 3

Por lo tanto, el mensaje fue enviado por el propietario de la clave privada y no se ha modificado desde que se firmó..

DSA pros & contras

La seguridad de DSA depende de si utiliza números adecuados. Además de p, q y sol respetando los parámetros correctos, el valor de k También debe ser aleatorio. No debe ser un valor predecible o un valor que se use varias veces. Si no se cumplen estos requisitos, un atacante puede recuperar la clave.

A pesar de esta posibilidad, El DSA generalmente se considera seguro siempre que se implemente correctamente y use valores adecuados. Aunque es relativamente seguro, DSA no tiende a implementarse mucho en comparación con RSA u otros métodos de firma digital. En comparación con RSA, puede generar claves más rápido y también es más rápido para generar firmas digitales, pero más lento para verificarlas.

La versión 7.0 de OpenSSH dejó de admitir claves DSA de forma predeterminada, lo que parece ser una señal de que el mundo está pasando de DSA a otros algoritmos.

ECDSA & EdDSA

RSA y DSA no son los únicos algoritmos de firma digital, ni son los más adecuados para todas las situaciones. Hay una variedad de otros, como ECDSA y EdDSA, que tienen propiedades que los hacen preferibles en ciertas circunstancias.

Desafortunadamente, estos se basan en matemáticas aún más complicadas, como la curva elíptica y la criptografía de la curva de Edwards. No los cubriremos en detalle hoy debido a esta complejidad adicional, pero hablaremos sobre algunos de sus posibles aspectos positivos y negativos..

ECDSA

El algoritmo de firma digital de curva elíptica es una variación de DSA que incorpora criptografía de curva elíptica. Proporciona un nivel de seguridad similar al RSA, pero con una clave mucho más pequeña. Esto lo hace más eficiente que RSA o DSA en la mayoría de los aspectos del rendimiento.

EdDSA

Esta es otra alternativa DSA, excepto que se basa en curvas Twisted Edwards. Es relativamente nuevo en lo que respecta a los algoritmos, lo que tiene sus ventajas y desventajas. En el lado positivo, utiliza técnicas más nuevas que se suman a su rendimiento..

Desafortunadamente, los algoritmos más nuevos no han estado expuestos a tanto escrutinio, por lo que muchas personas son cautelosas al decidir si implementarlos o no..

A pesar de esto, el uso de EdDSA proporciona un alto nivel de rendimiento, resistencia a los ataques de canal lateral, y elimina la necesidad de un número aleatorio único en cada firma. En esta etapa, EdDSA parece prometedor y está comenzando a ver una implementación más amplia, pero tendremos que esperar y ver si futuros estudios encuentran algún agujero de seguridad.

Certificados digitales

Cualquiera puede hacer fácilmente un par de llaves, incluso un atacante. Entonces, ¿qué evita que alguien haga un montón de llaves y pretenda que es el Presidente, o que se haga pasar por otra persona??

Bueno, nada impide que alguien afirme que es otra persona, pero existe un sistema que permite a los demás determinar si la persona realmente es o no quien dice ser. Se llama el infraestructura de clave pública (PKI), e implica certificados digitales que vinculan la clave pública de una persona o entidad con su verdadera identidad. Estos certificados están firmados por otros para indicar cuánto se debe confiar en el certificado.

Puede comparar el proceso con el uso de notarios para verificar documentos. Si alguien tiene una copia de un certificado de nacimiento, puede ser escéptico sobre si es legítimo o no. Si ese mismo acta de nacimiento fue firmada y sellada por un notario, sería mucho más probable que crea que es una copia real.

Por qué?

Debido a que la firma y el sello muestran que una entidad pública de confianza ha visto al individuo y su certificado de nacimiento original, verificó que la copia es de hecho legítima. El notario valida la copia del certificado de nacimiento y confirma su reputación con su firma y sello..

La confianza que tenemos para el notario se transfiere a la copia del certificado de nacimiento, lo que nos permite confiar en mucho más que uno que no ha sido notariado..

Hay dos tipos principales de certificación, cAutoridades de certificación (CA) y la red de confianza.

Autoridades de certificación

Las autoridades de certificación son organizaciones confiables que realizan verificaciones de personas o entidades para verificar si son el propietario legítimo de una clave pública. Si los cheques revelan que el individuo es el verdadero propietario, la autoridad certificadora firmará el certificado con su propia clave, lo que significa que ha completado el cheque y cree que la clave individual y pública están legítimamente vinculadas.

Siempre y cuando confiemos en la autoridad de certificación y su proceso de verificación de la clave, podemos confiar en un certificado firmado por ellos., y así la clave pública realmente representa a ese individuo.

Dependiendo del tipo de certificado y su aplicación, los diferentes niveles pueden tener diferentes procesos de verificación y, por lo tanto, representan un mayor o menor grado de confianza..

La red de confianza

La red de confianza opera bajo una premisa similar, excepto taquí no hay cuerpos centrales como autoridades de certificación que realizan el proceso de verificación y firman los certificados.

En cambio, la red de confianza se basa en que otras personas firmen certificados, apostando su reputación en el enlace entre la clave individual y la pública. Este sistema se usa principalmente con PGP, donde los usuarios pueden hacer fácilmente sus propios certificados.

Funciona así:

Supongamos que tiene dos amigos que desean firmar sus certificados para demostrar que son los propietarios legítimos de sus respectivas claves públicas. Conoces bien a estas personas y te muestran sus identificaciones gubernamentales, lo que te hace absolutamente seguro de que son quienes dicen ser y, por lo tanto, son los verdaderos propietarios de las claves públicas que reclaman..

Como sabe que son los propietarios legítimos de sus claves públicas, le complace usar su clave privada para firmar sus certificados, apostando su reputación y esencialmente diciendo “Sí, he verificado las identidades de estas personas y son quienes son ellos dicen ser “. Estos dos amigos pueden hacer lo mismo contigo.

Supongamos que cada uno de tus dos amigos tiene otros dos amigos que desean firmar sus certificados. Si sus dos amigos firman estos otros certificados, entonces puede usar la confianza que tiene en sus amigos para aceptar que estas otras personas son realmente quienes dicen ser también.

Los amigos de tus amigos pueden firmar los certificados de las personas en las que confían y así sucesivamente, eventualmente construyendo una gran red de personas de confianza. Una vez que estas redes crecen lo suficiente y se interconectan con otras redes, se pueden usar como un medio para confiar en cualquier otra persona en la red.

Cuantas más firmas hay en un certificado, especialmente si son firmas de personas altamente confiables, cuanto más pueda confiar en el certificado digital de alguien y el vínculo entre su clave pública y su identidad.

Los usuarios de PGP con frecuencia celebran fiestas de firma clave donde las personas se congregan para verificar sus identidades y firmar sus certificados digitales. Estas reuniones ayudan a atraer nuevas personas a la red..

Aunque viene con algunas complejidades, la ventaja del sistema de red de confianza es que no hay un cuerpo central que pueda corromperse.

¿Son seguras las firmas digitales??

En un sentido general, las firmas digitales son seguras a menos que la clave privada del firmante haya sido comprometida. Si el propietario ha informado a otra persona, ha dejado la clave privada escrita o la ha robado de otra manera, entonces es posible que un atacante firme digitalmente los mensajes como si fuera el propietario.

Esto puede hacer que el atacante se haga pasar por su víctima o manipule sus datos. Este es un gran problema de seguridad, y cualquier persona que sospeche que su clave ha sido comprometida debe revocar su certificado digital que los vincula a su clave pública y emitir uno nuevo..

Hay algunas otras advertencias cuando se trata de la seguridad de las firmas digitales. Se debe utilizar un algoritmo de firma digital apropiado, y también debe implementarse correctamente. Además de esto, también debe existir una forma de vincular la clave pública con su propietario, generalmente a través de certificados digitales.

Mientras se cumplan estos requisitos, está siguiendo las mejores prácticas de la industria y su clave privada no se ha visto comprometida, entonces Las firmas digitales son una excelente manera de proporcionar autenticidad, integridad y no repudio a los datos..

Datos estructurados por Kai Stachowiak bajo licencia CC0