¿Qué es el intercambio de claves Diffie-Hellman y cómo funciona?

El intercambio de claves Diffie-Hellman fue uno de los desarrollos más importantes en criptografía de clave pública y todavía se implementa con frecuencia en una variedad de protocolos de seguridad diferentes de la actualidad.

Permite que dos partes que no se hayan reunido previamente establezcan una clave que puedan usar para asegurar sus comunicaciones. En este artículo, explicaremos para qué se utiliza, cómo funciona paso a paso, sus diferentes variaciones, así como las consideraciones de seguridad que deben tenerse en cuenta para implementarlo de manera segura.

¿Qué es el intercambio de claves Diffie-Hellman??

El intercambio de claves Diffie-Hellman fue el primer método ampliamente utilizado para desarrollar e intercambiar claves de manera segura a través de un canal inseguro.

Puede que no parezca tan emocionante o innovador en los términos anteriores, así que vamos a dar un ejemplo que explica por qué el intercambio de claves Diffie-Hellman fue un hito tan importante en el mundo de la criptografía y por qué todavía se usa con tanta frecuencia hoy.

Supongamos que es un espía de alto secreto y necesita enviar información importante a su sede. ¿Cómo evitarías que tus enemigos reciban el mensaje??

La solución más común sería cifrar el mensaje con un código. La forma más fácil es organizar previamente cualquier tipo de código y clave que planee usar de antemano, o hacerlo a través de un canal de comunicación seguro.

Digamos que usted es un espía particularmente malo, y usted y su cuartel general deciden usar un código de cambio débil para codificar sus mensajes. En este código, cada “a” se convierte en “b”, cada “b” se convierte en “c”, cada “c” se convierte en “d”, y así sucesivamente, hasta la “z” se convierte en una “a”.

Bajo este cifrado de turno, el mensaje “Vamos a cenar” se convierte en “Mfu’t hfu ejoofs”. Afortunadamente, en nuestra situación hipotética, sus adversarios son tan incompetentes como usted y no pueden descifrar un código tan simple que les impide acceder al contenido del mensaje..

Pero, ¿qué sucede si no puede organizar un código con su destinatario de antemano??

Supongamos que quiere comunicarse con un espía de una nación aliada que nunca antes había conocido. No tienes un canal seguro para hablar con ellos. Si no cifra su mensaje, cualquier adversario que lo intercepte podrá leer el contenido. Si lo encriptas sin decirle al aliado el código, entonces el enemigo no podrá leerlo, pero tampoco lo hará el aliado..

Este problema fue uno de los mayores acertijos en criptografía hasta la década de 1970:

¿Cómo puede intercambiar información de manera segura con alguien si no ha tenido la oportunidad de compartir la clave con anticipación??

El intercambio de claves Diffie-Hellman fue el primer mecanismo utilizado públicamente para resolver este problema. El algoritmo permite a aquellos que nunca se conocieron crear una clave compartida de manera segura, incluso a través de un canal inseguro que los adversarios pueden estar monitoreando.

La historia del intercambio de claves Diffie-Hellman

El intercambio de claves Diffie-Hellman tiene sus raíces en la década de 1970. Si bien el campo de la criptografía se había desarrollado significativamente a lo largo del siglo XX, estos avances se centraron principalmente en el área de la criptografía de clave simétrica.

No fue sino hasta 1976 que surgieron algoritmos de clave pública en la esfera pública, cuando Whitfield Diffie y Martin Hellman publicaron su artículo., Nuevas direcciones en criptografía. La colaboración describió los mecanismos detrás de un nuevo sistema, que se conocería como el Intercambio de llaves Diffie-Hellman.

El trabajo se inspiró en parte en desarrollos anteriores realizados por Ralph Merkle. La llamada Rompecabezas de Merkle involucrar a una parte creando y enviando una serie de acertijos criptográficos a la otra. Estos rompecabezas tomarían una cantidad moderada de recursos computacionales para resolver.

El destinatario elegiría aleatoriamente un rompecabezas para resolver y luego gastaría el esfuerzo necesario para completarlo. Una vez que se resuelve el rompecabezas, se revela un identificador y una clave de sesión al destinatario. El destinatario luego transmite el identificador al remitente original, lo que le permite saber qué rompecabezas se ha resuelto.

Como el remitente original creó los rompecabezas, el identificador les permite saber qué clave de sesión descubrió el destinatario, y las dos partes pueden usar esta clave para comunicarse de manera más segura. Si un atacante está escuchando la interacción, tendrá acceso a todos los rompecabezas, así como al identificador que el destinatario transmite al remitente original..

El identificador no le dice al atacante qué clave de sesión se está utilizando, por lo que el mejor enfoque para descifrar la información es resuelve todos los rompecabezas para descubrir la clave de sesión correcta. Como el atacante tendrá que resolver la mitad de los acertijos en promedio, resulta mucho más difícil para ellos descubrir la clave que para el destinatario.

Este enfoque proporciona más seguridad, pero está lejos de ser una solución perfecta. El intercambio de claves Diffie-Hellman tomó algunas de estas ideas y las hizo más complejas para crear un método seguro de criptografía de clave pública.

Aunque se conoce como el intercambio de claves Diffie-Hellman, Martin Hellman ha propuesto que el algoritmo se denomine intercambio de claves Diffie-Hellman-Merkle en su lugar, para reflejar el trabajo que Ralph Merkle realizó hacia la criptografía de clave pública.

Se pensó públicamente que Merkle, Hellman y Diffie fueron las primeras personas en desarrollar criptografía de clave pública hasta 1997, cuando el Gobierno británico desclasificó el trabajo realizado a principios de la década de 1970 por James Ellis, Clifford Cox y Malcolm Williamson.

Resulta que al trío se le ocurrió el primer esquema de cifrado de clave pública entre 1969 y 1973, pero su trabajo se clasificó durante dos décadas. Se realizó bajo la sede de Comunicación del Gobierno (GCHQ), una agencia de inteligencia del Reino Unido..

Su descubrimiento fue en realidad el algoritmo RSA, por lo que Diffie, Hellman y Merkle fueron los primeros en desarrollar el intercambio de claves Diffie-Hellman, pero ya no fueron los primeros inventores de la criptografía de clave pública..

¿Dónde se utiliza el intercambio de claves Diffie-Hellman??

El objetivo principal del intercambio de claves Diffie-Hellman es Desarrolle de manera segura secretos compartidos que puedan usarse para derivar claves. Estas claves se pueden usar con algoritmos de clave simétrica para transmitir información de manera protegida. Los algoritmos simétricos tienden a usarse para encriptar la mayor parte de los datos porque son más eficientes que los algoritmos de clave pública.

Técnicamente, el intercambio de claves Diffie-Hellman se puede utilizar para establecer claves públicas y privadas. Sin embargo, en la práctica, RSA tiende a usarse en su lugar. Esto se debe a que el algoritmo RSA también es capaz de firmar certificados de clave pública, mientras que el intercambio de claves Diffie-Hellman no es.

El algoritmo ElGamal, que se utilizó mucho en PGP, se basa en el intercambio de claves Diffie-Hellman, por lo que cualquier protocolo que lo use está implementando efectivamente un tipo de Diffie-Hellman.

Como uno de los métodos más comunes para distribuir claves de manera segura, el intercambio de claves Diffie-Hellman es implementado con frecuencia en protocolos de seguridad como TLS, IPsec, SSH, PGP y muchos otros. Esto lo convierte en una parte integral de nuestras comunicaciones seguras..

Como parte de estos protocolos, el intercambio de claves Diffie-Hellman se usa a menudo para ayudar a asegurar su conexión a un sitio web, para acceder de forma remota a otra computadora y para enviar correos electrónicos cifrados

¿Cómo funciona el intercambio de claves Diffie-Hellman??

El intercambio de claves Diffie-Hellman es complejo y puede ser difícil entender cómo funciona.. Utiliza números muy grandes y muchas matemáticas., algo que muchos de nosotros aún tememos de esas largas y aburridas lecciones de secundaria.

Para hacer las cosas un poco más fáciles de entender., comenzaremos explicando el intercambio de claves Diffie-Hellman con una analogía. Una vez que tenga una idea general de cómo funciona, pasaremos a una descripción más técnica de los procesos subyacentes..

La mejor analogía para el esquema Diffie-Hellman es pensar en dos personas mezclando pintura. Usemos el estándar de criptografía y digamos que sus nombres son Alice y Bob. Ambos acuerdan un color aleatorio para comenzar. Digamos que se envían un mensaje y decidir sobre el amarillo como su color común, al igual que en el siguiente diagrama:

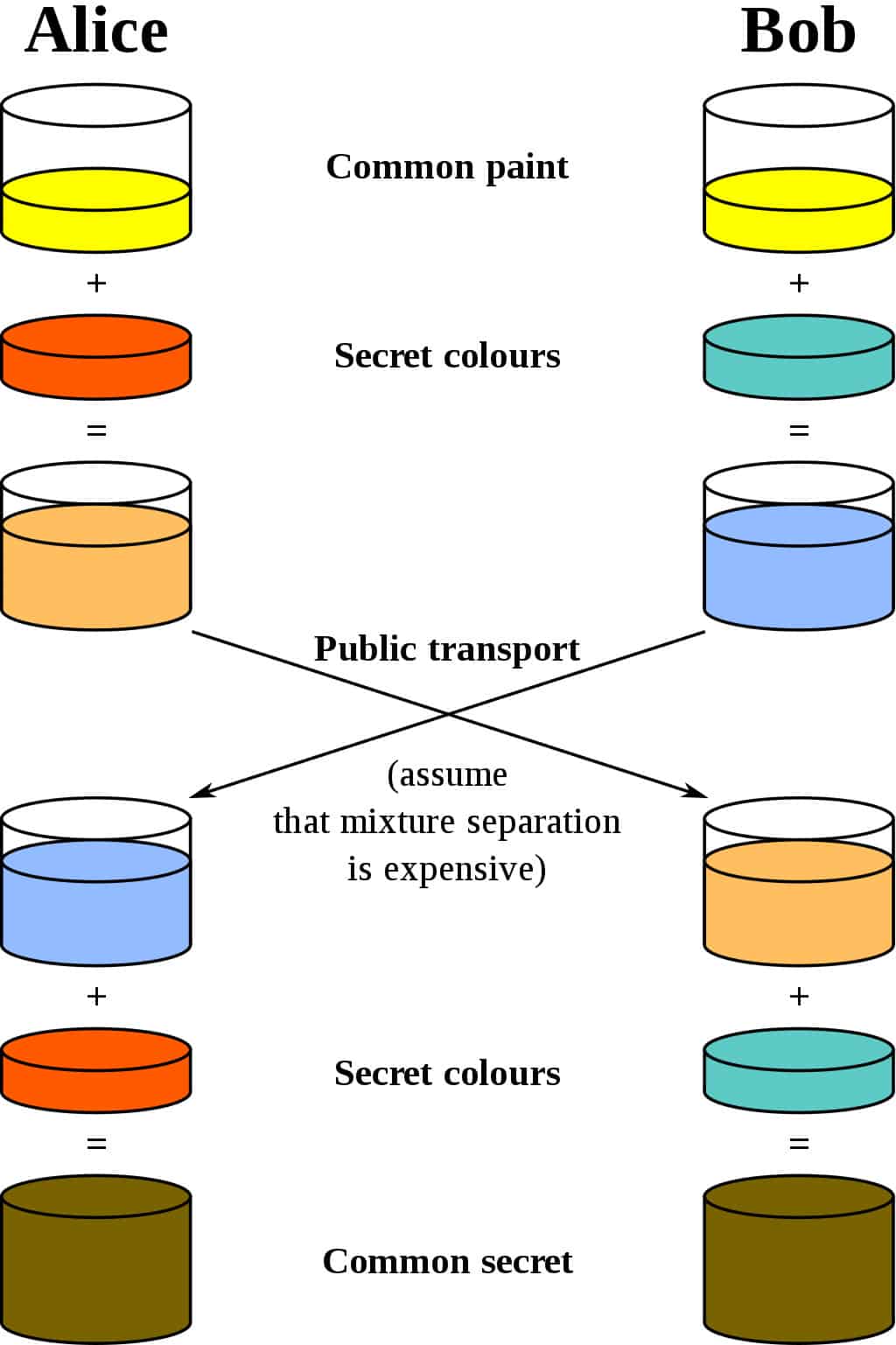
se su propio color secreto. No le dicen a la otra parte su elección. Digamos que Alice elige rojo, mientras Bob elige un azul ligeramente verdoso.

El siguiente paso es que tanto Alice como Bob mezclen su color secreto (rojo para Alice, azul verdoso para Bob) con el amarillo que acordaron mutuamente. Según el diagrama, Alice termina con un mezcla anaranjada, mientras que el resultado de Bob es un azul más profundo.

Una vez que han terminado la mezcla, envían el resultado a la otra parte.. Alice recibe el azul más profundo, mientras Bob recibe la pintura de color naranja..

Una vez que han recibido el resultado mixto de su compañero, le agregan su color secreto. Alice toma el azul más profundo y agrega su pintura roja secreta, mientras Bob agrega su secreto azul verdoso a la mezcla de naranja que acaba de recibir.

El resultado? Ambos salen con el mismo color., que en este caso es de un marrón repugnante. Puede que no sea el tipo de color con el que desearía pintar su sala de estar, pero no obstante es un color compartido. Este color compartido se conoce como secreto común.

La parte crítica del intercambio de claves Diffie-Hellman es que ambas partes terminan con el mismo resultado, sin necesidad de enviar la totalidad del secreto común a través del canal de comunicación.. Elegir un color común, sus propios colores secretos, intercambiar la mezcla y luego agregar su propio color una vez más, brinda a ambas partes una forma de llegar al mismo secreto común sin tener que enviar todo el asunto..

Si un atacante está escuchando el intercambio, todo lo que puede acceder es el color amarillo común con el que comienzan Alice y Bob, así como los colores mezclados que se intercambian. Como esto realmente se hace con números enormes en lugar de pintura, estos datos no son suficientes para que el ataque discierna los colores secretos iniciales o el secreto común (técnicamente es posible calcular el secreto común a partir de esta información, pero en una implementación segura del intercambio de claves Diffie-Hellman, tomaría una cantidad inviable de tiempo y recursos computacionales para hacerlo).

Esta estructura del intercambio de claves Diffie-Hellman es lo que lo hace tan útil. Permite que las dos partes se comuniquen a través de una conexión potencialmente peligrosa y aún así encontrar un secreto compartido que pueden usar para crear claves de cifrado para sus futuras comunicaciones.. No importa si algún atacante está escuchando, porque el secreto compartido completo nunca se envía a través de la conexión.

Los detalles técnicos del intercambio de claves Diffie-Hellman

Tiempo para algunas matemáticas …

No se preocupe, lo tomaremos con calma e intentaremos que todo el proceso sea lo más fácil de entender posible. Sigue una premisa similar a la analogía que se muestra arriba, pero en lugar de mezclar y enviar colores, el esquema Diffie-Hellman en realidad hace cálculos basados ​​en números primos excepcionalmente grandes, luego los envía.

Para garantizar la seguridad, se recomienda que el principal (pag) tiene al menos 2048 bits de longitud, que es el equivalente binario de un número decimal de aproximadamente este tamaño:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

Para evitar que explote la cabeza de alguien, ejecutaremos esta explicación con números mucho más pequeños. Sé consciente de el intercambio de claves Diffie-Hellman sería inseguro si utilizara números tan pequeños como los de nuestro ejemplo. Solo estamos usando números tan pequeños para demostrar el concepto de una manera más simple.

En la forma más básica del intercambio de claves Diffie-Hellman, Alice y Bob comienzan decidiendo mutuamente dos números para comenzar, a diferencia de la pintura común única en el ejemplo anterior. Estos son el módulo (pag) y la base (sol).

En uso práctico, el módulo (p) es un número primo muy grande, mientras la base (sol) es relativamente pequeño para simplificar los cálculos. La base (sol) se deriva de un grupo cíclico (sol) que normalmente se genera mucho antes de que se realicen los otros pasos.

Para nuestro ejemplo, digamos que el módulo (pag) es 17, mientras que la basesol) es 4 4.

Una vez que se han decidido por estos números, Alice se decide por un número secreto (un) para ella, mientras Bob elige su propio número secreto (si) Digamos que eligen:

a = 3

b = 6

Luego, Alice realiza el siguiente cálculo para darle el número que le enviará a Bob:

A = ga mod p

En el cálculo anterior, modificación significa una operación de módulo. Estos son esencialmente cálculos para calcular el resto después de dividir el lado izquierdo por el derecho. Como ejemplo:

15 mod 4 = 3

Si comprende cómo funcionan las operaciones de módulo, puede hacerlo usted mismo en los siguientes cálculos; de lo contrario, puede usar una calculadora en línea.

Así que pongamos nuestros números en la fórmula:

A = 43 mod 17

A = 64 mod 17

A = 13

Cuando hacemos lo mismo para Bob, obtenemos:

B = 46 mod 17

B = 4096 mod 17

B = 16

Alice luego envía su resultado (UN) a Bob, mientras Bob envía su figura (si) a Alice. Luego, Alice calcula el secreto compartido (s) utilizando el número que recibió de Bob (si) y su número secreto (un), utilizando la siguiente fórmula:

s = Ba mod pag

s = 163 mod 17

s = 4,096 mod 17

s = 16

Bob luego realiza lo que es esencialmente el mismo cálculo, pero con el número que Alice le envió (UN), así como su propio número secreto (si):

s = UNsi modificación pag

s = 136 mod 17

s = 4,826,809 mod 17

s = 16

Como puede ver, ambas partes terminaron con el mismo resultado para s, dieciséis. Este es el secreto compartido, que solo Alice y Bob conocen. Luego pueden usar esto para configurar una clave para el cifrado simétrico, lo que les permite enviar información de forma segura entre ellos de una manera que solo ellos puedan acceder..

Tenga en cuenta que aunque si y s son los mismos en el ejemplo anterior, esto es solo una coincidencia basada en los pequeños números elegidos para esta ilustración. Normalmente, estos valores no serían los mismos en una implementación real del intercambio de claves Diffie-Hellman.

Aunque gran parte de los datos anteriores se envían a través del canal en texto sin cifrar (p, g, A y si) y pueden ser leídos por posibles atacantes, el secreto compartido (s) nunca se transmite. No sería práctico para un atacante calcular el secreto compartido (s) o cualquiera de los números secretos (un y si) de la información que se envía en texto sin cifrar.

Por supuesto, esto supone que el intercambio de claves Diffie-Hellman se implementa correctamente y se utilizan números suficientemente grandes. Mientras se cumplan estas disposiciones, el intercambio de claves Diffie-Hellman se considera una forma segura de establecer un secreto compartido que se puede utilizar para asegurar futuras comunicaciones..

Establecer una clave compartida entre múltiples partes

El intercambio de claves Diffie-Hellman también se puede utilizar para configurar una clave compartida con un mayor número de participantes. Funciona de la misma manera, excepto que se necesitan más rondas de los cálculos para que cada parte agregue su número secreto y termine con el mismo secreto compartido.

Al igual que en la versión de dos partes del intercambio de claves Diffie-Hellman, algunas partes de la información se envían a través de canales inseguros, pero no lo suficiente como para que un atacante pueda calcular el secreto compartido.

¿Por qué es seguro el intercambio de claves Diffie-Hellman??

A nivel matemático, el intercambio de claves Diffie-Hellman se basa en funciones unidireccionales como base para su seguridad. Estos son cálculos que son simples de hacer de una manera, pero mucho más difíciles de calcular a la inversa.

Más específicamente, se basa en el problema de Diffie-Hellman, que supone que bajo los parámetros correctos, no es factible calcular solab de los valores separados de sol, solun y solsi. Actualmente no existe una forma públicamente conocida de encontrar fácilmente solab de los otros valores, por lo que el intercambio de claves Diffie-Hellman se considera seguro, a pesar de que los atacantes pueden interceptar los valores pag, sol, UN, y si.

Autenticación & el intercambio de llaves Diffie-Hellman

En el mundo real, el intercambio de claves Diffie-Hellman rara vez se usa solo. La razón principal detrás de esto es que no proporciona autenticación, lo que deja a los usuarios vulnerables a los ataques de intermediarios.

Estos ataques pueden tener lugar cuando el intercambio de claves Diffie-Hellman se implementa solo, porque no tiene forma de verificar si la otra parte en una conexión es realmente quien dice ser. Sin ninguna forma de autenticación, los usuarios pueden estar conectando con atacantes cuando piensan que se están comunicando con una parte confiable.

Por esta razón, el intercambio de claves Diffie-Hellman generalmente se implementa junto con algunos medios de autenticación. Esto a menudo implica el uso de certificados digitales y un algoritmo de clave pública, como RSA, para verificar la identidad de cada parte.

Variaciones del intercambio de claves Diffie-Hellman

El intercambio de claves Diffie-Hellman se puede implementar de varias maneras diferentes, y también ha proporcionado la base para varios otros algoritmos. Algunas de estas implementaciones proporcionan autorización, mientras que otras tienen varias características criptográficas, como el perfecto secreto directo.

Curva elíptica Diffie-Hellman

Curva elíptica Diffie-Hellman aprovecha la estructura algebraica de las curvas elípticas para permitir que sus implementaciones alcancen un nivel de seguridad similar con un tamaño de clave más pequeño. Una clave de curva elíptica de 224 bits proporciona el mismo nivel de seguridad que una clave RSA de 2048 bits. Esto puede hacer que los intercambios sean más eficientes y reducir los requisitos de almacenamiento..

Además de la menor longitud de la clave y el hecho de que se basa en las propiedades de las curvas elípticas, la curva elíptica Diffie-Hellman funciona de manera similar al intercambio de claves estándar Diffie-Hellman.

TLS   

TLS, que es un protocolo que se utiliza para proteger gran parte de Internet, puede usar el intercambio Diffie-Hellman de tres maneras diferentes: anónimo, estático y efímero. En la práctica, solo se debe implementar el efímero Diffie-Hellman, porque las otras opciones tienen problemas de seguridad.

• Anónimo Diffie-Hellman – Esta versión del intercambio de claves Diffie-Hellman no utiliza ninguna autenticación, dejándola vulnerable a los ataques de intermediarios. No debe ser usado o implementado.
• Diffie-Hellman estático – Static Diffie-Hellman usa certificados para autenticar el servidor. No autentica al cliente de manera predeterminada, ni proporciona confidencialidad.
• Efímero Diffie-Hellman – Esta se considera la implementación más segura porque proporciona un perfecto secreto hacia adelante. Generalmente se combina con un algoritmo como DSA o RSA para autenticar a una o ambas partes en la conexión. Efímero Diffie-Hellman utiliza diferentes pares de claves cada vez que se ejecuta el protocolo. Esto proporciona a la conexión un secreto perfecto, porque incluso si una clave se ve comprometida en el futuro, no se puede usar para descifrar todos los mensajes pasados..

ElGamal

ElGamal es un algoritmo de clave pública construido sobre el intercambio de claves Diffie-Hellman. Al igual que Diffie-Hellman, no contiene disposiciones para la autenticación por sí solo, y generalmente se combina con otros mecanismos para este propósito..

ElGamal se utilizó principalmente en PGP, GNU Privacy Guard y otros sistemas porque su principal rival, RSA, estaba patentado. La patente de RSA expiró en 2000, lo que permitió que se implementara libremente después de esa fecha. Desde entonces, ElGamal no se ha implementado con tanta frecuencia.

STS

El protocolo de estación a estación (STS) también se basa en el intercambio de claves Diffie-Hellman. Es otro esquema de acuerdo clave, sin embargo, proporciona protección contra ataques de intermediarios, así como un perfecto secreto hacia adelante..

Requiere que ambas partes en la conexión ya tengan un par de claves, que se utiliza para autenticar cada lado. Si las partes aún no se conocen, entonces los certificados se pueden usar para validar las identidades de ambas partes.

El intercambio de llaves Diffie-Hellman & RSA

Como discutimos anteriormente, El intercambio de claves Diffie-Hellman a menudo se implementa junto con RSA u otros algoritmos para proporcionar autenticación para la conexión. Si está familiarizado con RSA, es posible que se pregunte por qué alguien se molestaría en usar el intercambio de claves Diffie-Hellman también, ya que RSA permite que las partes que nunca se hayan conocido se comuniquen de manera segura.

RSA permite a sus usuarios cifrar mensajes con la clave pública de sus corresponsales, de modo que solo puedan ser descifrados por la clave privada correspondiente. Sin embargo, en la práctica, RSA no se usa para encriptar la totalidad de las comunicaciones; esto sería demasiado ineficiente.

En cambio, RSA a menudo solo se usa como un medio para autenticar a ambas partes. Hace esto con los certificados digitales de cada parte, que habrán sido verificados por una autoridad de certificación para demostrar que el propietario de un certificado es realmente quien dice ser, y que la clave pública del certificado realmente les pertenece.

Para autenticación mutua, cada parte firmará un mensaje usando su clave privada y luego lo enviará a su socio de comunicación. Cada destinatario puede entonces verificar la identidad de la otra parte comprobando los mensajes firmados con la clave pública en el certificado digital de su socio de comunicación (consulte el artículo mencionado anteriormente sobre RSA para obtener más detalles sobre cómo funciona esto, particularmente el Firmando mensajes sección).

Ahora que ambas partes han sido autenticadas, es técnicamente posible continuar usando RSA para enviar mensajes cifrados de forma segura entre ellos, sin embargo, terminaría siendo demasiado ineficiente.

Para evitar esta ineficiencia, muchos protocolos de seguridad utilizan un algoritmo como el intercambio de claves Diffie-Hellman para encontrar un secreto común que se pueda utilizar para establecer una clave simétrica compartida. Esta clave simétrica se utiliza en un algoritmo de clave simétrica, como AES, para cifrar los datos. que las dos partes tienen la intención de enviar de forma segura entre ellas.

Puede parecer un proceso complejo y complicado, pero termina siendo mucho más rápido y menos exigente en recursos en comparación con el uso de un algoritmo de clave pública para todo el intercambio. Esto es porque el cifrado de clave simétrica es un orden de magnitud más eficiente que el cifrado de clave pública.

Además de las ineficiencias que acabamos de mencionar, existen otras desventajas que se derivarían únicamente del uso de RSA. RSA necesita relleno para que sea seguro, entonces un algoritmo adicional necesitaría ser implementado apropiadamente junto a él para hacerlo seguro.

RSA no proporciona un secreto directo perfecto, tampoco, lo cual es otra desventaja en comparación con el intercambio de claves efímero Diffie-Hellman. Colectivamente, estas razones son la razón por la cual, en muchas situaciones, es mejor solo aplicar RSA junto con el intercambio de claves Diffie-Hellman.

Alternativamente, el intercambio de claves Diffie-Hellman se puede combinar con un algoritmo como el estándar de firma digital (DSS) para proporcionar autenticación, intercambio de claves, confidencialidad y verificar la integridad de los datos. En tal situación, RSA no es necesario para asegurar la conexión.

Problemas de seguridad del intercambio de claves Diffie-Hellman

La seguridad del intercambio de claves Diffie-Hellman depende de cómo se implemente, así como de los números que se elijan para ello. Como dijimos anteriormente, no tiene medios para autenticar a la otra parte por sí misma, pero en la práctica se utilizan otros mecanismos para garantizar que la otra parte en una conexión no sea un impostor.

Parámetros para la selección de números.

Si una implementación en el mundo real del intercambio de claves Diffie-Hellman usara números tan pequeños como los de nuestro ejemplo, haría que el proceso de intercambio sea trivial para que un atacante descifre. Pero lo importante no es solo el tamaño de los números: los números también deben ser suficientemente aleatorios. Si un generador de números aleatorios produce una salida predecible, puede socavar por completo la seguridad del intercambio de claves Diffie-Hellman.

El número pag debe tener 2048 bits de largo para garantizar la seguridad. La base, sol, puede ser un número relativamente pequeño como 2, pero tiene que venir de un orden de sol que tiene un gran factor primo

El ataque Logjam

El intercambio de claves Diffie-Hellman fue diseñado sobre la base del problema de logaritmo discreto que es difícil de resolver. El mecanismo más efectivo conocido públicamente para encontrar la solución es el algoritmo de tamizado de campo numérico.

Las capacidades de este algoritmo se tuvieron en cuenta cuando se diseñó el intercambio de claves Diffie-Hellman. En 1992, se sabía que para un grupo dado, sol, tres de los cuatro pasos involucrados en el algoritmo podrían calcularse de antemano. Si este progreso se guardó, el paso final podría calcularse en un tiempo relativamente corto.

Esto no fue demasiado preocupante hasta que se dio cuenta de que una parte significativa del tráfico de Internet utiliza los mismos grupos que son de 1024 bits o menos. En 2015, un equipo académico realizó los cálculos para el primo de 512 bits más común utilizado por el intercambio de claves Diffie-Hellman en TLS.

También pudieron degradar el 80% de los servidores TLS que admitían DHE-EXPORT, por lo que aceptarían un intercambio de claves Diffie-Hellman de 512 bits para la conexión. Esto significa que cada uno de estos servidores es vulnerable a un ataque de un adversario con buenos recursos.

Los investigadores continuaron extrapolando sus resultados, estimando que un estado-nación podría romper un primo de 1024 bits. Al romper el primer formato de 1024 bits más utilizado, el equipo académico estimó que un adversario podría monitorear el 18% de los millones de sitios web HTTPS más populares.

Continuaron diciendo que una segunda función principal permitiría al adversario descifrar las conexiones del 66% de los servidores VPN y el 26% de los servidores SSH. Más adelante en el informe, los académicos sugirieron que la NSA ya puede tener estas capacidades.

“Una lectura detallada de las filtraciones de la NSA publicadas muestra que los ataques de la agencia a las VPN son consistentes con haber logrado tal interrupción”.

A pesar de esta vulnerabilidad, el intercambio de claves Diffie-Hellman aún puede ser seguro si se implementa correctamente. Mientras se use una clave de 2048 bits, el ataque Logjam no funcionará. Los navegadores actualizados también están seguros de este ataque.

¿Es seguro el intercambio de claves Diffie-Hellman??

Si bien el intercambio de claves Diffie-Hellman puede parecer complejo, es una parte fundamental del intercambio seguro de datos en línea. Siempre que se implemente junto con un método de autenticación apropiado y los números se hayan seleccionado correctamente, no se considera vulnerable a los ataques..

El intercambio de claves Diffie-Hellman fue un método innovador para ayudar a dos partes desconocidas a comunicarse de manera segura cuando se desarrolló en la década de 1970. Si bien ahora implementamos versiones más nuevas con teclas más grandes para proteger contra la tecnología moderna el protocolo en sí parece que seguirá siendo seguro hasta la llegada de la computación cuántica y los ataques avanzados que vendrán con él.

Tecnología empresarial de ciberseguridad por TheDigitalArtist con licencia bajo CC0