¿Qué es el cifrado RSA y cómo funciona?

El cifrado RSA es un sistema que resuelve lo que alguna vez fue uno de los mayores problemas en criptografía: ¿Cómo puedes enviar un mensaje codificado a alguien? sin tener la oportunidad de compartir previamente el código con ellos?

Este artículo le enseñará todo lo que necesita saber. cómo se desarrolló el cifrado RSA, cómo funciona, las matemáticas detrás de esto, para que se utiliza así como algunas de las mayores problemas de seguridad que enfrenta. Aprender acerca de RSA le dará un conocimiento fundamental que lo ayudará a comprender cuántas partes de nuestra vida en línea se mantienen seguras.

¿Qué es el cifrado RSA??

Digamos que quieres contarle a tu amigo un secreto. Si estás justo al lado de ellos, puedes susurrarlo. Si estás en lados opuestos del país, eso obviamente no funcionará. Puede escribirlo y enviárselo por correo, o usar el teléfono, pero cada uno de estos canales de comunicación es inseguro y cualquiera con una motivación lo suficientemente fuerte podría interceptar fácilmente el mensaje.

Si el secreto fuera lo suficientemente importante, no se arriesgaría a escribirlo normalmente: espías o un empleado postal no autorizado podría estar revisando su correo. Del mismo modo, alguien podría estar tocando su teléfono sin su conocimiento y registrando cada llamada que realiza.

Una solución para evitar que los espías accedan al contenido del mensaje es encriptarlo. Esto básicamente significa agregar un código al mensaje que lo convierte en un desorden desordenado. Si su código es lo suficientemente complejo, las únicas personas que podrán acceder al mensaje original son aquellas que tienen acceso al código..

Si tuvo la oportunidad de compartir el código con su amigo de antemano, entonces cualquiera de ustedes puede enviar un mensaje cifrado en cualquier momento, sabiendo que ustedes dos son los únicos con la capacidad de leer el contenido del mensaje. Pero, ¿qué pasaría si no tuvieras la oportunidad de compartir el código de antemano??

Este es uno de los problemas fundamentales de la criptografía, que ha sido abordado por esquemas de cifrado de clave pública (también conocido como cifrado asimétrico) como RSA.

Bajo el cifrado RSA, los mensajes se cifran con un código llamado Llave pública, que se puede compartir abiertamente. Debido a algunas propiedades matemáticas distintas del algoritmo RSA, una vez que un mensaje ha sido encriptado con la clave pública, solo puede ser desencriptado por otra clave, conocida como la clave privada. Cada usuario de RSA tiene un par de claves que consta de sus claves públicas y privadas. Como su nombre indica, la clave privada debe mantenerse en secreto..

Los esquemas de cifrado de clave pública difieren de cifrado de clave simétrica, donde el proceso de cifrado y descifrado utiliza la misma clave privada. Estas diferencias hacen que el cifrado de clave pública como RSA sea útil para comunicarse en situaciones donde no ha habido oportunidad de distribuir claves de forma segura de antemano.

Los algoritmos de clave simétrica tienen sus propias aplicaciones, como el cifrado de datos para uso personal o cuando hay canales seguros en los que las claves privadas se pueden compartir.

Ver también: Criptografía de clave pública

¿Dónde se usa el cifrado RSA??

El cifrado RSA se usa a menudo en combinación con otros esquemas de encriptación, o por firmas digitales que puede probar la autenticidad e integridad de un mensaje. Generalmente no se usa para cifrar mensajes o archivos completos, porque es menos eficiente y requiere más recursos que el cifrado de clave simétrica.

Para hacer las cosas más eficientes., un archivo generalmente se cifrará con un algoritmo de clave simétrica, y luego la clave simétrica se cifrará con cifrado RSA. Bajo este proceso, solo una entidad que tenga acceso a la clave privada RSA podrá descifrar la clave simétrica.

Sin poder acceder a la clave simétrica, el el archivo original no se puede descifrar. Este método se puede utilizar para mantener seguros los mensajes y archivos, sin demorar demasiado o consumir demasiados recursos computacionales..

El cifrado RSA se puede usar en varios sistemas diferentes. Se puede implementar en OpenSSL, wolfCrypt, cryptlib y otras bibliotecas criptográficas..

Como uno de los primeros esquemas de cifrado de clave pública ampliamente utilizados, RSA sentó las bases de muchas de nuestras comunicaciones seguras. Era utilizado tradicionalmente en TLS y también fue el algoritmo original utilizado en el cifrado PGP. RSA todavía se ve en una variedad de navegadores web, correo electrónico, VPN, chat y otros canales de comunicación..

RSA también se usa a menudo para hacer conexiones seguras entre clientes VPN y servidores VPN. Bajo protocolos como OpenVPN, los apretones de manos TLS pueden usar el algoritmo RSA para intercambiar claves y establecer un canal seguro.

Los antecedentes del cifrado RSA

Como mencionamos al comienzo de este artículo, antes del cifrado de clave pública, era un desafío comunicarse de forma segura si no hubiera existido la posibilidad de intercambiar claves de forma segura de antemano. Si no hubiera una oportunidad de compartir el código antes de tiempo, o un canal seguro a través del cual se pudieran distribuir las claves, no habría forma de comunicarse sin la amenaza de que los enemigos pudieran interceptar y acceder al contenido del mensaje.

No fue hasta la década de 1970 que las cosas realmente comenzaron a cambiar. El primer desarrollo importante hacia lo que ahora llamamos criptografía de clave pública fue publicado a principios de la década por James H. Ellis. Ellis no pudo encontrar una manera de implementar su trabajo, pero su colega Clifford Cocks lo amplió para convertirse en lo que ahora conocemos como Cifrado RSA.

La pieza final del rompecabezas es lo que ahora llamamos el Intercambio de llaves Diffie-Hellman. Malcolm J. Williamson, otro compañero de trabajo, descubrió un esquema que permitía a dos partes compartir una clave de cifrado, incluso si el canal estaba siendo monitoreado por adversarios.

Todo este trabajo se llevó a cabo en la agencia de inteligencia del Reino Unido, la Oficina Central de Comunicaciones del Gobierno (GCHQ), que mantuvo el descubrimiento clasificado. En parte debido a limitaciones tecnológicas, el GCHQ no podía ver el uso de la criptografía de clave pública en ese momento, por lo que el desarrollo se detuvo en el estante acumulando polvo. No fue sino hasta 1997 que el trabajo fue desclasificado y se reconoció a los inventores originales de RSA.

Varios años después, conceptos similares comenzaron a desarrollarse en la esfera pública. Ralph Merkle creó una forma temprana de criptografía de clave pública, que influyó en Whitfield Diffie y Martin Hellman en el diseño del intercambio de claves Diffie-Hellman.

A las ideas de Diffie y Hellman les faltaba un aspecto importante que haría de su trabajo una base de la criptografía de clave pública. Esto fue un función unidireccional que sería difícil de invertir. En 1977, Ron Rivest, Adi Shamir y Leonard Adleman, cuyos apellidos forman el acrónimo RSA, encontraron una solución después de un año de trabajar en el problema.

Los académicos del MIT hicieron su gran avance después de una fiesta de Pascua en 1977. Después de una noche de beber, Rivest se fue a su casa, pero en lugar de dormir, pasó la tarde escribiendo febrilmente un periódico que formalizaba su idea para la función unidireccional necesaria..

La idea fue patentada en 1983 por el MIT, pero no fue hasta los primeros días de Internet que el algoritmo RSA comenzó a ver la adopción generalizada como una herramienta de seguridad importante..

¿Cómo funciona el cifrado RSA??

La siguiente será una simplificación, ya que muchos maestros de escuela secundaria probablemente han dejado cicatrices. Para evitar que las matemáticas se salgan de control, estaremos simplificando algunos conceptos y usando números mucho más pequeños. En realidad, el cifrado RSA usa números primos que son mucho más grandes en magnitud y hay algunas otras complejidades.

Hay varios conceptos diferentes que tendrá que entender antes de que podamos explicar cómo encaja todo. Éstos incluyen funciones de trampillas, generación de números primos, función totient de Carmichael y los procesos separados involucrados en calcular las claves públicas y privadas utilizado en los procesos de cifrado y descifrado.

Funciones de trampillas

El cifrado RSA funciona bajo la premisa de que el algoritmo es fácil de calcular en una dirección, pero casi imposible en reversa. Como ejemplo, si le dijeran que 701,111 es un producto de dos números primos, ¿podría averiguar cuáles son esos dos números??

Incluso con una calculadora o una computadora, la mayoría de nosotros no tendríamos idea de por dónde empezar, y mucho menos podríamos encontrar la respuesta. Pero si volteamos las cosas, se vuelve mucho más fácil. ¿Cuál es el resultado de:

907 x 773

Si estuvieras lo suficientemente aburrido, podrías haber sacado tu teléfono o tal vez calcularlo en tu cabeza para descubrir que la respuesta es el 701,111 mencionado anteriormente. Este 907 y 773 son los números primos que responden a nuestra primera pregunta, lo que nos muestra que ciertas ecuaciones pueden ser fáciles de resolver de una manera, pero aparentemente imposibles a la inversa.

Otro aspecto interesante de esta ecuación es que es simple descubrir uno de los números primos si ya tiene el otro, así como el producto. Si le dicen que 701,111 es el resultado de 907 multiplicado por otro número primo, puede calcular el otro primo con la siguiente ecuación:

701.111 ÷ 907 = 773

Dado que la relación entre estos números es simple de calcular en una dirección, pero increíblemente difícil a la inversa, la ecuación se conoce como función de trampilla. Tenga en cuenta que si bien el ejemplo anterior es difícil de entender para las personas, las computadoras pueden realizar la operación en un período de tiempo trivial.

Debido a esto, RSA usa números mucho más grandes. El tamaño de los primos en una implementación RSA real varía, pero en un RSA de 2048 bits, se unirían para crear claves de 617 dígitos. Para ayudarlo a visualizarlo, una clave sería un número de este tamaño:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Generando primos

Las funciones de trampillas mencionadas anteriormente forman la base de cómo funcionan los esquemas de cifrado de clave pública y privada. Sus propiedades permiten compartir claves públicas sin poner en peligro el mensaje o revelar la clave privada.. También permiten que los datos se cifren con una clave de una manera que solo la otra clave del par pueda descifrar..

El primer paso para cifrar un mensaje con RSA es generar las llaves. Para hacer esto, necesitamos dos números primos (pag y q) que se seleccionan con una prueba de primalidad. Una prueba de primalidad es un algoritmo que encuentra eficientemente números primos, como la prueba de primalidad Rabin-Miller.

Los números primos en RSA deben ser muy grandes y también relativamente separados. Los números que son pequeños o más cercanos son mucho más fáciles de descifrar. A pesar de esto, nuestro ejemplo usará números más pequeños para hacer que las cosas sean más fáciles de seguir y calcular.

Digamos que la prueba de primalidad nos da los números primos que usamos anteriormente, 907 y 773. El siguiente paso es descubrir el módulo (norte), utilizando la siguiente fórmula:

norte = pag X q

Dónde pag = 907 y q = 773

Por lo tanto:

norte = 907 x 773

norte = 701,111

La función totient de Carmichael

Una vez que tengamos norte, usamos La función totient de Carmichael:

    λ(norte) = mcm (pag – 1, q – 1)

Si ha pasado un tiempo desde que llegó a los libros de texto de matemáticas, lo anterior puede parecer un poco aterrador. Puede omitir esta parte y confiar en que las matemáticas funcionan, de lo contrario, quédese con nosotros para algunos cálculos más. Todo se explicará con el mayor detalle posible para ayudarlo a entender los conceptos básicos..

Para aquellos que no están al tanto, λ (n) representa al paciente de Carmichael por norte, mientras mcm significa el mínimo común múltiplo, cual es el número más bajo que ambos pag y q puede dividirse en Hay algunas maneras diferentes de resolver esto, pero la más fácil es confiar en una calculadora en línea para que haga la ecuación por usted. Así que pongamos nuestros números en la ecuación:

    λ(701,111) = mcm (907 – 1, 773 – 1)

    λ(701,111) = mcm (906, 772)

   Usando la calculadora vinculada anteriormente, esto nos da:

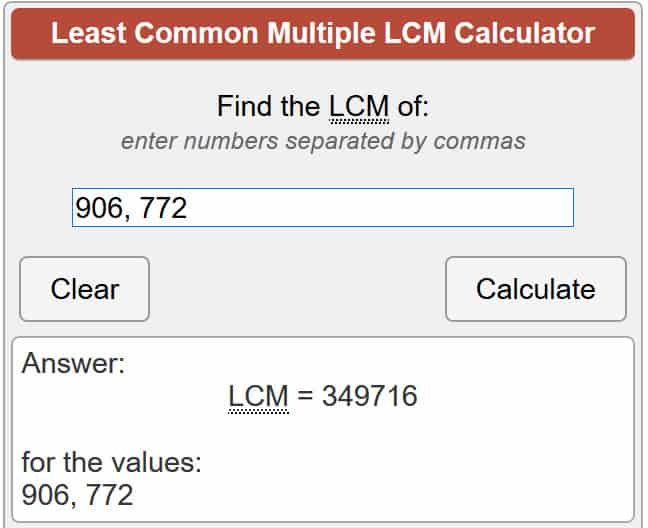
    λ(701,111) = 349,716

Generando la clave pública

Ahora que tenemos el total de nuestros números primos de Carmichael, es hora de descubrir nuestra clave pública. Bajo RSA, las claves públicas están formadas por un número primo mi, tanto como norte. El número mi puede ser cualquier cosa entre 1 y el valor de λ(norte), que en nuestro ejemplo es 349,716.

Debido a que la clave pública se comparte abiertamente, no es tan importante para mi ser un número aleatorio En la práctica, mi generalmente se establece en 65,537, porque cuando se eligen números mucho más grandes al azar, el cifrado es mucho menos eficiente. Para el ejemplo de hoy, mantendremos los números pequeños para que los cálculos sean eficientes. Digamos:

mi = 11

Nuestros datos cifrados finales se denominan texto cifrado (C) Lo derivamos de nuestro mensaje de texto sin formato (metro), aplicando la clave pública con la siguiente fórmula:

C = metromi mod n

Ya se nos ocurrió mi y sabemos norte también. Lo único que necesitamos explicar es modificación. Está un poco fuera de la profundidad de este artículo, pero se refiere a un operación de módulo, lo que esencialmente significa el resto sobrante cuando divide un lado por el otro. Por ejemplo:

10 modificación 3 = 1

Esto se debe a que 3 entra en 10 tres veces, con un resto de 1.

De vuelta a nuestra ecuación. Para simplificar las cosas, digamos que el mensaje (metro) que queremos cifrar y mantener en secreto es solo un número, 4 4. Enchufemos todo:

C = metromi modificación norte

C = 411 modificación 701,111

C = 4,194,304 modificación 701,111

De nuevo, para hacer el operación de módulo fácil, usaremos una calculadora en línea, pero puede averiguarlo usted mismo. Al ingresar 4,194,304 en la calculadora en línea, nos da:

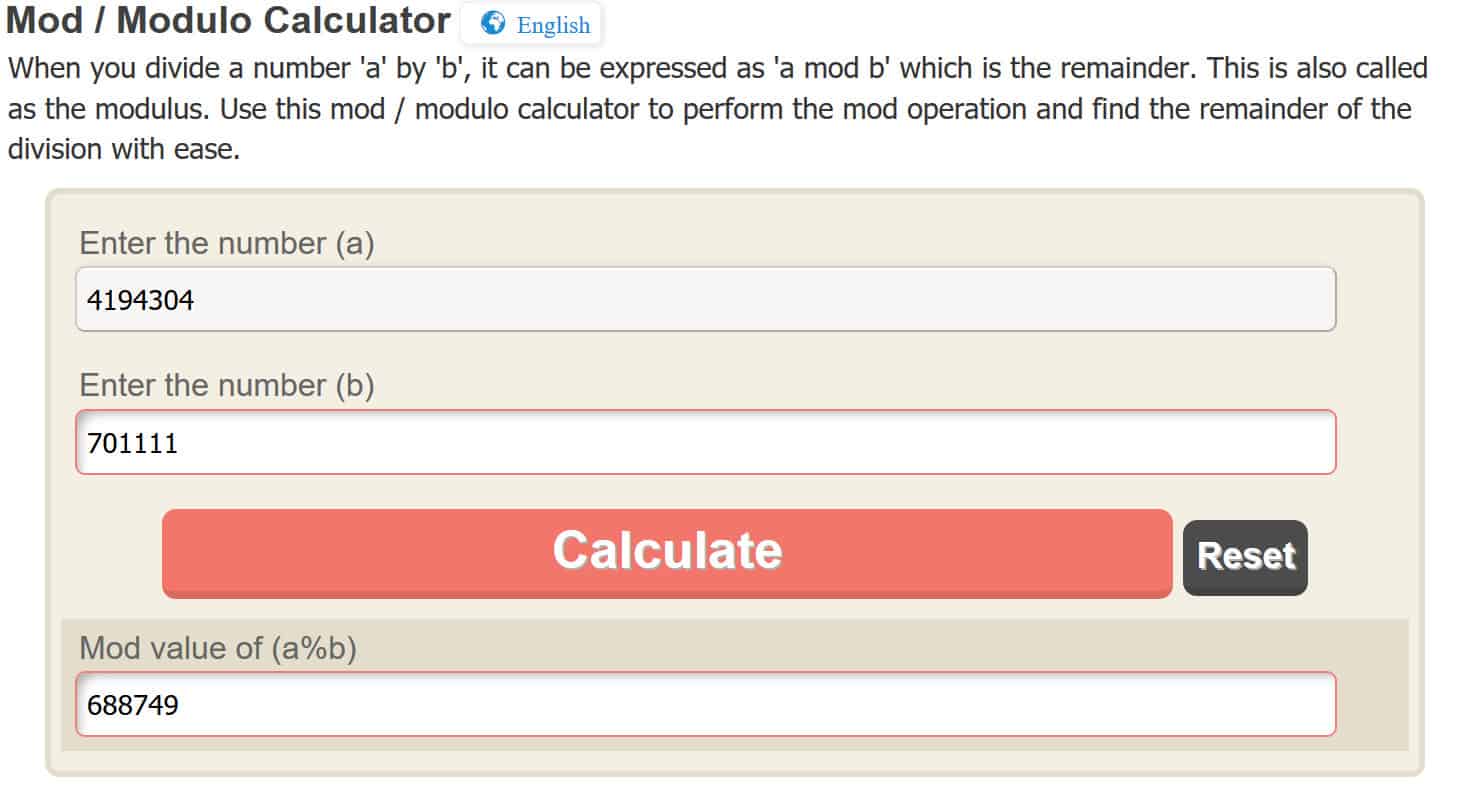
c = 688,749

Por lo tanto, cuando usamos RSA para cifrar nuestro mensaje, 4 4, con nuestra clave pública, nos da la texto cifrado de 688,749. Los pasos anteriores pueden haber parecido demasiado matemáticos, pero es importante reiterar lo que realmente sucedió.

Teniamos mensaje de 4, que queríamos mantener en secreto Le aplicamos una clave pública, lo que nos dio el resultado cifrado de 688,749. Ahora que está encriptado, podemos enviar de forma segura el número 688,749 al propietario del par de claves. Son la única persona que podrá descifrarlo con su clave privada. Cuando lo descifren, verán el mensaje que realmente estábamos enviando., 4 4.

Generando la clave privada

En el cifrado RSA, una vez que los datos o un mensaje se han convertido en texto cifrado con una clave pública, solo se puede descifrar mediante la clave privada del mismo par de claves.. Las claves privadas se componen de re y norte. Ya sabemos norte, y la siguiente ecuación se usa para encontrar re:

re = 1 /mi mod λ(norte)

En el Generando la clave pública sección anterior, ya decidimos que en nuestro ejemplo, mi sería igual a 11. De manera similar, sabemos que λ(norte) es igual a 349,716 de nuestro trabajo anterior bajo La función totient de Carmichael. Las cosas se ponen un poco más complicadas cuando nos encontramos con esta sección de la fórmula:

1 /mi modificación

Puede parecer que esta ecuación le pide que divida 1 entre 11, pero ese no es el caso. En cambio, esto solo simboliza que necesitamos calcular el inversa modular de mi (que en este caso es 11) y λ(norte) (que en este caso es 349,716).

Esto esencialmente significa que en lugar de realizar una operación de módulo estándar, usaremos la inversa. Esto normalmente se encuentra con el Algoritmo Euclidiano Extendido, pero está un poco fuera del alcance de este artículo, por lo que solo haremos trampa y usaremos una calculadora en línea. Ahora que entendemos todo lo que está sucediendo, conectemos nuestra información a la fórmula:

re = 1 /11 modificación 349,716

Para realizar esta operación, simplemente ingrese 11 (o cualquier valor que pueda tener para mi si está intentando esto con su propio ejemplo) donde dice Entero y 349,716 (o cualquier valor que pueda tener para λ(norte) si está intentando esto con su propio ejemplo) donde dice Módulo en la calculadora en línea que estaba vinculada anteriormente. Si lo ha hecho correctamente, debería obtener un resultado donde:

re = 254, 339

Ahora que tenemos el valor para re, Podemos descifrar los mensajes que se cifraron con nuestra clave pública utilizando la siguiente fórmula:

metro = Cre mod n

Ahora podemos volver al texto cifrado que ciframos bajo el Generando la clave privada sección. Cuando ciframos el mensaje con la clave pública, nos dio un valor para C de 688,749. Desde arriba, sabemos que re es igual a 254,339. También sabemos que norte es igual a 701,111. Esto nos da:

metro = 688,749254,339 modificación 701,111.

Como habrás notado, tratar de llevar un número a la potencia 254,339 podría ser un poco demasiado para la mayoría de las calculadoras normales. En su lugar, utilizaremos una calculadora de descifrado RSA en línea. Si quisiera utilizar otro método, aplicaría los poderes como lo haría normalmente y realizaría la operación de módulo de la misma manera que lo hicimos en el Generando la clave pública sección.

En la calculadora vinculada anteriormente, ingrese 701,111 donde dice Módulo de suministro: N, 254,399 donde dice Clave de descifrado: D, y 688,749 donde dice Mensaje de texto cifrado en forma numérica, Como se muestra abajo:

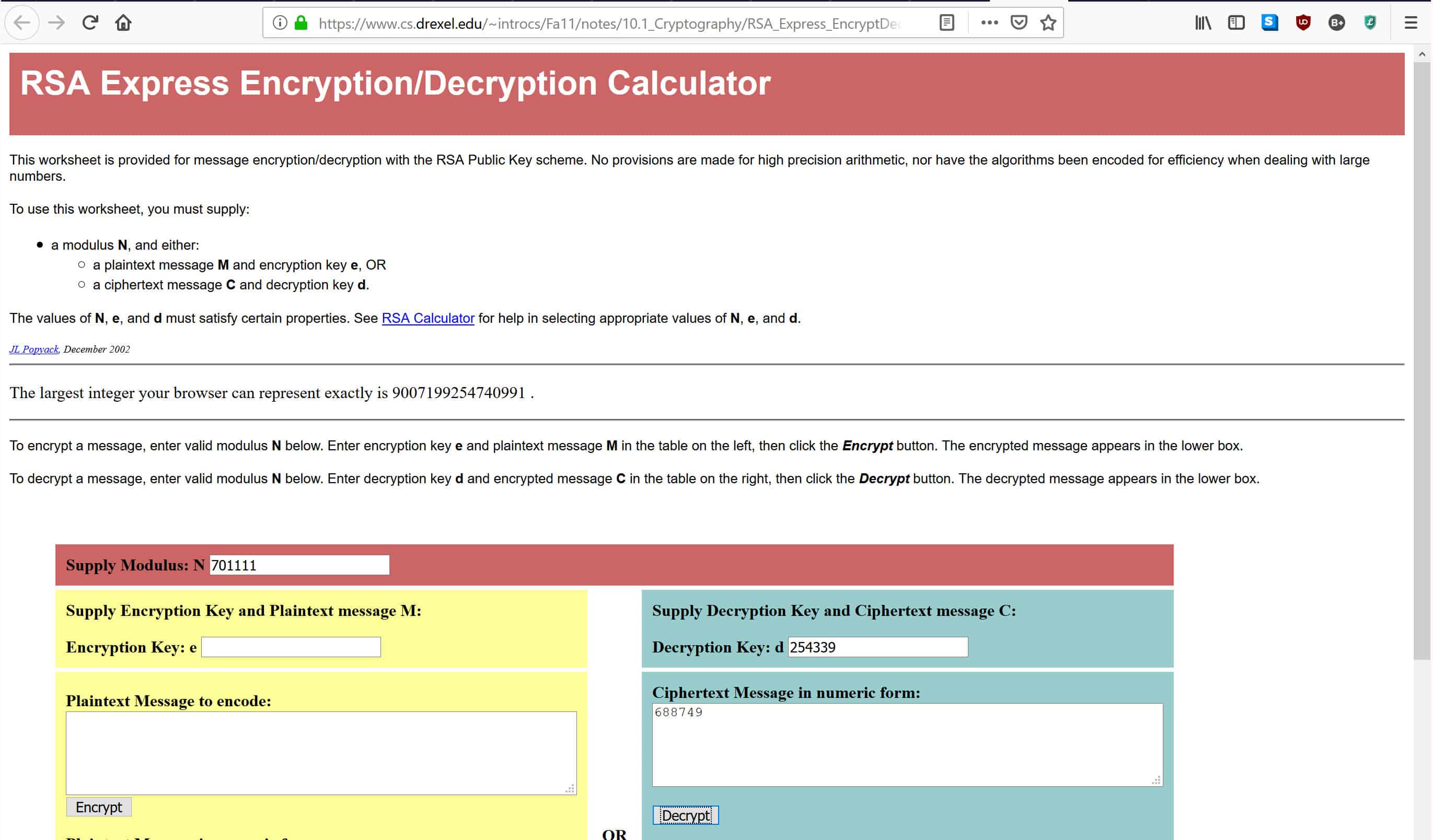
Una vez que haya ingresado los datos, presione Descifrar, que pondrá los números a través de la fórmula de descifrado que se enumeró anteriormente. Esto le dará el mensaje original en el cuadro a continuación. Si ha hecho todo correctamente, debería obtener una respuesta de 4 4, que era el mensaje original que ciframos con nuestra clave pública.

Cómo funciona el cifrado RSA en la práctica

Las secciones anteriores deberían darle una idea razonable de cómo funcionan las matemáticas detrás del cifrado de clave pública. Puede ser un poco confuso, pero incluso aquellos que no entendieron las complejidades de las ecuaciones pueden, con suerte, extraer información importante sobre el proceso..

En los pasos enumerados anteriormente, hemos mostrado cómo dos entidades pueden comunicarse de forma segura sin haber compartido previamente un código. Primero, cada uno necesita configurar sus propios pares de claves y compartir la clave pública entre sí. Las dos entidades deben mantener sus claves privadas en secreto para que sus comunicaciones permanezcan seguras.

Una vez que el remitente tiene la clave pública de su destinatario, puede usarla para cifrar los datos que desea mantener seguros. Una vez que se ha cifrado con una clave pública, solo se puede descifrar con la clave privada del mismo par de claves.. Incluso la misma clave pública no se puede usar para descifrar los datos. Esto se debe a las propiedades de funciones de trampillas que mencionamos anteriormente.

Cuando el destinatario recibe el mensaje cifrado, usa su clave privada para acceder a los datos. Si el destinatario desea devolver las comunicaciones de forma segura, luego pueden cifrar su mensaje con la clave pública de la parte con la que se están comunicando. Una vez más, una vez que se ha cifrado con la clave pública, la única forma de acceder a la información es a través de la clave privada correspondiente..

De esta manera, el cifrado RSA puede ser utilizado por partes previamente desconocidas para enviar datos de forma segura entre ellos. Partes importantes de los canales de comunicación que utilizamos en nuestras vidas en línea se construyeron a partir de esta base..

¿Cómo se cifran los mensajes más complicados con RSA??

En nuestro ejemplo, simplificamos mucho las cosas para que sea más fácil de entender, por lo que solo ciframos un mensaje de “4”. Ser capaz de cifrar el número 4 no parece particularmente útil, por lo que puede que se pregunte cómo puedes encriptar un conjunto de datos más complicado, como una clave simétrica (que es el uso más común de RSA) o incluso un mensaje.

Algunas personas pueden estar perplejas de cómo una clave como “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” o un mensaje como “cómprame un sandwich” puede encriptarse mediante un algoritmo como RSA, que trata con números y no con letras. La realidad es que toda la información que procesan nuestras computadoras se almacena en binario (1s y 0s) y usamos estándares de codificación como ASCII o Unicode para representarlos de manera que los humanos puedan entender (letras).

Esto significa que teclas como “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” y mensajes como “cómprame un sandwich” ya existen como números, que se puede calcular fácilmente en el algoritmo RSA. Los números que representan son mucho más grandes y difíciles de manejar, por lo que preferimos tratar con caracteres alfanuméricos en lugar de una mezcla de binarios..

Si quieres cifrar una clave de sesión más larga o un mensaje más complejo con RSA, simplemente implicaría un número mucho mayor.

Relleno

Cuando se implementa RSA, usa algo llamado relleno para ayudar a prevenir una serie de ataques. Para explicar cómo funciona esto, comenzaremos con un ejemplo. Digamos que estaba enviando un mensaje codificado a un amigo:

Querida karen,

    Espero que estés bien. ¿Aún cenaremos mañana??

    Tuyo sinceramente,

    James

Digamos que codificó el mensaje de una manera simple, por cambiando cada letra a la que le sigue en el alfabeto. Esto cambiaría el mensaje a:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

Si tus enemigos interceptaron esta carta, hay un truco que podrían usar para intentar descifrar el código. Ellos podrían mira el formato de tu carta e intenta adivinar lo que el mensaje podría estar diciendo. Saben que las personas normalmente comienzan sus letras con “Hola”, “Hola”, “Estimado” o una serie de otras convenciones.

Si intentaran aplicar “Hola” o “Hola” como la primera palabra, verían que no encajaría en la cantidad de caracteres. Entonces podrían probar “Estimado”. Se ajusta, pero eso no significa necesariamente nada. Los atacantes lo intentarían y verían a dónde los conducía. Entonces, cambiarían las letras “e”, “f”, “b” y “s” con “d”, “e”, “a” y “r” respectivamente. Esto les daría:

Querido Laseo,

    J ipqe zpv son xemm. Are xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

Todavía se ve bastante confuso, por lo que los atacantes podrían intentar mirar algunas otras convenciones, como concluimos nuestras cartas. La gente a menudo agrega “De” o “Saludos cordiales” al final, pero ninguno de estos se ajusta al formato. En cambio, los atacantes podrían intentar “Atentamente” y reemplazar las otras letras para ver dónde las consigue. Al cambiar “z”, “p”, “v”, “t”, “j”, “o”, “d” y “m” con “y”, “o”, “u”, “s”, ” i “,” n “,” c “y” l “respectivamente, obtendrían:

Querida Lasen,

    Yo sé que tú eres Xell. Son xe tuill iawinh dinnes uonossox?

    Tuyo sinceramente,

    Kanet

Después de esa modificación, parece que los atacantes están comenzando a llegar a algún lado. Han encontrado las palabras “yo”, “usted” y “son”, además de las palabras que hicieron sus conjeturas iniciales.

Al ver que las palabras están en el orden gramatical correcto, los atacantes pueden estar bastante seguros de que se dirigen en la dirección correcta. A estas alturas, probablemente también se hayan dado cuenta de que el código implicaba que cada letra se cambiara por la que sigue en el alfabeto.. Una vez que se dan cuenta de esto, es fácil traducir el resto y leer el mensaje original..

El ejemplo anterior era solo un código simple, pero como puede ver, la estructura de un mensaje puede dar pistas a los atacantes sobre su contenido. Claro, fue difícil descifrar el mensaje solo por su estructura y tomó algunas conjeturas educadas, pero debe tener en cuenta que las computadoras son mucho mejores para hacer esto que nosotros.. Esto significa que se pueden usar para descubrir códigos mucho más complejos en un tiempo mucho más corto, basado en pistas que provienen de la estructura y otros elementos.

Si la estructura puede hacer que se descifre un código y revelar el contenido de un mensaje, entonces necesitamos alguna forma de ocultar la estructura para mantener el mensaje seguro. Esto nos lleva a relleno.

Cuando se rellena un mensaje, Se agregan datos aleatorizados para ocultar las pistas de formato originales que podrían provocar la ruptura de un mensaje cifrado. Con RSA, las cosas son un poco más complicadas, porque una clave cifrada no tiene el formato obvio de una carta que nos ayudó a darnos pistas en nuestro ejemplo anterior..

A pesar de esto, los adversarios pueden usar varios ataques para explotar las propiedades matemáticas de un código y romper datos cifrados. Debido a esta amenaza, Las implementaciones de RSA utilizan esquemas de relleno como OAEP para incrustar datos adicionales en el mensaje. Agregar este relleno antes de que se cifre el mensaje hace que RSA sea mucho más seguro.

Firmando mensajes

RSA puede usarse para algo más que solo cifrar datos. Sus propiedades también lo convierten en un sistema útil para confirmando que un mensaje ha sido enviado por la entidad que afirma haberlo enviado, y comprobando que un mensaje no ha sido alterado o manipulado.

Cuando alguien quiere demostrar la autenticidad de su mensaje, puede calcular un picadillo (una función que toma datos de un tamaño arbitrario y los convierte en un valor de longitud fija) del texto sin formato, luego lo firma con su clave privada. Ellos firmar el hash aplicando la misma fórmula que se utiliza en el descifrado (m = cre mod n) Una vez que el mensaje ha sido firmado, envían esta firma digital al destinatario junto con el mensaje.

Si un destinatario recibe un mensaje con una firma digital, puede usar el firma para verificar si el mensaje fue firmado auténticamente por la clave privada de la persona que dice haberlo enviado. También pueden ver si los atacantes han cambiado el mensaje después de haberlo enviado..

Para verificar la firma digital, el destinatario primero usa la misma función hash para encontrar el valor hash del mensaje que recibió. El destinatario aplica entonces el clave pública del remitente a la firma digital, usando la fórmula de cifrado (c = mmi mod n), para darles el hash de la firma digital.

Por Comparar el hash del mensaje recibido junto con el hash de la firma digital cifrada, el destinatario puede saber si el mensaje es auténtico. Si los dos valores son iguales, el mensaje no ha cambiado desde que se firmó por el remitente original. Si el mensaje hubiera sido alterado incluso por un solo carácter, el valor hash sería completamente diferente.

Seguridad RSA & ataques

Como la mayoría de los sistemas criptográficos, la seguridad de RSA depende de cómo se implemente y use. Un factor importante es el tamaño de la clave. los cuanto mayor es el número de bits en una clave (esencialmente cuánto dura la clave), más difícil es descifrar los ataques como la fuerza bruta y el factoraje.

Dado que los algoritmos de clave asimétrica como RSA pueden romperse mediante la factorización de enteros, mientras que los algoritmos de clave simétrica como AES no pueden, las claves RSA deben ser mucho más largas para lograr el mismo nivel de seguridad.

Actualmente, el El tamaño de clave más grande que se ha factorizado es de 768 bits de largo. Esto fue realizado por un equipo de académicos durante un período de dos años, utilizando cientos de máquinas..

Dado que la factorización se completó a fines de 2009 y la potencia de cómputo ha crecido significativamente desde entonces, se puede suponer que un intento de intensidad similar ahora podría factorizar una clave RSA mucho más grande.

A pesar de esto, el tiempo y los recursos necesarios para este tipo de ataque lo ponen fuera del alcance de la mayoría de los hackers y en el ámbito de los estados nacionales. La mejor longitud de clave a utilizar dependerá de su modelo de amenaza individual. El Instituto Nacional de Estándares y Tecnología. recomienda un tamaño de clave mínimo de 2048 bits, pero también se usan claves de 4096 bits en algunas situaciones donde el nivel de amenaza es más alto.

El factoring es solo una de las formas en que RSA puede romperse. Varios otros ataques tienen el potencial de romper el cifrado con una cantidad menor de recursos, pero estos dependen de la implementación y otros factores, no necesariamente del propio RSA. Algunos de estos incluyen:

¿Son los números primos realmente aleatorios??

Algunas implementaciones de RSA utilizan generadores de números aleatorios débiles para obtener los números primos. Si estos números no son lo suficientemente aleatorios, es mucho más fácil para los atacantes factorizarlos y romper el cifrado. Este problema puede evitarse utilizando un generador de números pseudoaleatorios criptográficamente seguro.

Mala generación de claves

Las claves RSA deben estar dentro de ciertos parámetros para que sean seguras. Si los primos pag y q están demasiado juntos, la clave se puede descubrir fácilmente. Del mismo modo, el número re que forma parte de la clave privada no puede ser demasiado pequeña. Un valor bajo hace que sea fácil de resolver. Es importante que estos números tengan la longitud adecuada para mantener su clave segura.

Ataques de canal lateral

Estos son un tipo de ataque que no interrumpe el RSA directamente, sino que utiliza la información de su implementación para dar a los atacantes pistas sobre el proceso de cifrado. Estos ataques pueden incluir cosas como analizar la cantidad de energía que se está utilizando, o análisis de predicción de rama, que utiliza mediciones de tiempo de ejecución para descubrir la clave privada.

Otro tipo de ataque de canal lateral se conoce como ataque de tiempo. Si un atacante tiene la capacidad de medir el tiempo de descifrado en la computadora de su objetivo para una cantidad de mensajes cifrados diferentes, Esta información puede hacer posible que el atacante determine la clave privada del objetivo.

La mayoría de las implementaciones de RSA evitan este ataque al agregar un valor único durante el proceso de cifrado, lo que elimina esta correlación. Este proceso se llama cegamiento criptográfico.

¿El cifrado RSA es seguro para el futuro??

La buena noticia es que RSA se considera seguro de usar, a pesar de estos posibles ataques. La advertencia es que debe implementarse correctamente y usar una clave que se encuentre dentro de los parámetros correctos. Como acabamos de comentar, las implementaciones que no usan relleno, usan primos de tamaño inadecuado o tienen otras vulnerabilidades no pueden considerarse seguras.

Si quieres usar encriptación RSA, asegúrese de utilizar una clave de al menos 1024 bits. Aquellos con modelos de mayor amenaza deben atenerse a claves de 2048 o 4096 bits si desean usar RSA con confianza. Mientras sea consciente de las debilidades que tiene RSA y lo use correctamente, debe sentirse seguro de usar RSA para compartir claves y otras tareas similares que requieren cifrado de clave pública.

Ver también: Tipos de cifrado comunes explicados