¿Qué es el cifrado 3DES y cómo funciona DES?

3DES es un cifrado de cifrado derivado del Estándar de cifrado de datos (DES) original. Se hizo prominente a fines de los noventa, pero desde entonces ha caído en desgracia debido al aumento de algoritmos más seguros.

Aunque quedará en desuso en 2023, todavía se implementa en algunas situaciones. Dado que se basa en uno de los primeros algoritmos ampliamente publicados y estudiados, DES, todavía es importante aprender qué es 3DES y cómo funciona.

Esta guía lo llevará a través de cada paso del proceso de DES en detalle, luego cubrirá cómo se modifica el DES en 3DES para hacerlo más seguro. También toca los diversos problemas de seguridad y si debe usar el algoritmo o no..

¿Qué es 3DES??

Aunque oficialmente se conoce como Algoritmo de cifrado de datos triple (3DEA), se le conoce comúnmente como 3DES. Esto se debe a que el algoritmo 3DES usa el cifrado del Estándar de cifrado de datos (DES) tres veces para cifrar sus datos.

DES es un algoritmo de clave simétrica basado en una red Feistel. Como cifrado de clave simétrica, utiliza la misma clave para los procesos de cifrado y descifrado. La red Feistel hace que ambos procesos sean casi exactamente iguales, lo que da como resultado un algoritmo que es más eficiente de implementar.

DES tiene un bloque de 64 bits y un tamaño de clave, pero en la práctica, la clave solo otorga 56 bits de seguridad. 3DES se desarrolló como una alternativa más segura debido a la pequeña longitud de la clave de DES. En 3DES, el algoritmo DES se ejecuta tres veces con tres claves, sin embargo, solo se considera seguro si se usan tres claves separadas.

Los usos de 3DES

Una vez que las debilidades del DES normal se hicieron más evidentes, se adoptó 3DES en una amplia gama de aplicaciones. Fue uno de los esquemas de cifrado más utilizados antes del surgimiento de AES.

Algunos ejemplos de sus implementaciones incluyen los sistemas de pago Microsoft Office, Firefox y EMV. Muchas de estas plataformas ya no usan 3DES porque hay mejores alternativas.

El Instituto Nacional de Estándares y Tecnología (NIST) ha publicado un borrador de propuesta que dice que todas las formas de 3DES quedarán en desuso hasta 2023 y se rechazarán a partir de 2024 en adelante. Aunque es solo un borrador, la propuesta significa el final de una era, y ya es hora de pasar a otros algoritmos más seguros.

La historia del cifrado 3DES

Dado que 3DES se deriva de DES, es mejor introducir primero el estándar anterior. En los años setenta, la Oficina Nacional de Estándares (NBS, por sus siglas en inglés) buscaba un algoritmo que pudiera usar como estándar para encriptar información gubernamental confidencial pero no clasificada..

La NBS aceptó propuestas para un estándar que se ajustara a sus requisitos, pero ninguno de los candidatos de la ronda original era apropiado. Invitó a más presentaciones, y esta vez IBM envió a través de un algoritmo que desarrolló su equipo. La sumisión se derivó del cifrado de Lucifer que Horst Feistel diseñó.

En 1975, el algoritmo de IBM fue publicado por la NBS como el Estándar de cifrado de datos propuesto. Se invitó al público a comentar sobre el diseño, lo que atrajo algunas críticas..

Criptógrafos prominentes como Whitfield Diffie y Martin Hellman, diseñadores del intercambio de claves Diffie-Hellman, afirmaron que la longitud de la clave era demasiado corta y que las cajas S habían cambiado desde su diseño inicial.

En ese momento, muchos en la comunidad criptográfica pensaron que la NSA había saboteado el proyecto y debilitado el algoritmo, por lo que sería la única agencia que podría romper DES.

Cuando esto fue investigado por el Comité Selecto de Inteligencia del Senado de los Estados Unidos, se descubrió que “la NSA convenció a IBM de que un tamaño de clave reducido era suficiente; indirectamente asistido en el desarrollo de las estructuras S-box; y certificó que el algoritmo final de DES estaba, a su leal saber y entender, libre de cualquier debilidad estadística o matemática “.

El mismo informe continuó diciendo que “la NSA no manipuló el diseño de ninguna manera”. Esto ha sido respaldado por algún antiguo personal de IBM que afirmó que el algoritmo DES fue diseñado completamente por el equipo de IBM.

La propia documentación desclasificada de la NSA afirma que la agencia “trabajó estrechamente con IBM para fortalecer el algoritmo contra todos excepto los ataques de fuerza bruta y para fortalecer las tablas de sustitución …”

Las sospechas de manipulación de la NSA disminuyeron en los años noventa una vez que se descubrió públicamente el criptoanálisis diferencial. Cuando se probaron las cajas S muy difamadas con la nueva técnica, se descubrió que eran más resistentes al ataque que si se hubieran elegido al azar.

Esto indica que el equipo de IBM ya sabía sobre el criptoanálisis diferencial en los años setenta, y Steven Levy afirmó que la NSA les pidió que mantuvieran la técnica en secreto para proteger la seguridad nacional..

El famoso criptógrafo Bruce Schneier bromeó una vez: “Le tomó a la comunidad académica dos décadas darse cuenta de que los” ajustes “de la NSA en realidad mejoraron la seguridad del DES”.

A pesar de las preguntas iniciales sobre la seguridad del algoritmo y la participación de la NSA, el algoritmo de IBM pasó a ser aprobado como el Estándar de cifrado de datos en 1976. Fue publicado en 1977 y reafirmado como el estándar en 1983, 1988 y 1993.

Cuando el criptoanálisis lineal se publicó por primera vez en 1994, comenzó a plantear preguntas sobre la seguridad del algoritmo. En 1997, NIST anunció que estaba buscando un algoritmo para reemplazar DES. La necesidad de un nuevo algoritmo se intensificó a medida que la tecnología se desarrolló aún más y los posibles ataques se hicieron más fuertes..

Varios intentos de craqueo mostraron que era menos difícil romper el algoritmo de lo que se pensaba anteriormente. En 1998, distribuido.net pudo descifrar DES hace 39 días..

A principios de 1999, Deep Crack de la Electronic Frontier Foundation había reducido el tiempo a poco más de 22 horas. Esto marcó el final de DES, ya que un ataque de esta naturaleza ahora estaba al alcance de un adversario con buenos recursos..

El problema principal era el pequeño espacio clave, y se necesitaba urgentemente un nuevo algoritmo. Esto era un problema, porque el NIST tardaría varios años más en decidirse por el algoritmo que se convirtió en el estándar de reemplazo, el Estándar de cifrado avanzado (AES).

Mientras se decidía el cifrado para AES, se propuso 3DES como una medida provisional. Implica ejecutar el algoritmo DES tres veces, con tres teclas separadas. En 1999, se reafirmó DES, pero con 3DES como el algoritmo ideal. El DES normal solo se permitía en aplicaciones heredadas.

3DES se convirtió en un algoritmo de cifrado generalizado, aunque su uso intensivo de recursos y limitaciones de seguridad han llevado a ser reemplazado por AES en la mayoría de los casos de uso..

Comprender el algoritmo DES

Antes de que podamos hablar sobre los detalles de 3DES, es importante comprender el algoritmo DES del que se deriva. Así que empecemos desde el principio.

Usamos cifrado para convertir nuestros datos de texto sin formato en texto cifrado, que es información a la que los atacantes no pueden acceder (siempre que utilicemos algoritmos apropiados).

Los algoritmos de cifrado son esencialmente fórmulas matemáticas complejas. Cuando se trata de encriptar algo como “Vamos a la playa”, muchas personas se confunden. Después de todo, ¿cómo puedes aplicar las matemáticas a cosas como letras y caracteres??

Codificando el texto

La realidad es que las computadoras no manejan letras y caracteres. En cambio, trabajan en un sistema de 1s y 0s conocido como binario. Cada 1 o 0 se conoce como un bit, y una colección de ocho de ellos se conoce como un byte.

Puede buscarlo manualmente o usar un convertidor en línea para ver que en binario, “Vamos a la playa” se convierte en:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

Bloques

Cuando los datos se cifran, se dividen en bloques separados para su procesamiento. DES tiene un tamaño de bloque de 64 bits, lo que esencialmente significa que cada bloque se ajusta a una mezcla de 64 unos y ceros. Nuestro primer bloque (los primeros 64 dígitos del binario que se muestra arriba) sería:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Nuestro segundo sería:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

Y nuestro bloque final sería:

01100010 01100101 01100001 01100011 01101000

Relleno

Es posible que haya notado que nuestro tercer bloque tiene solo 40 bits de longitud. Antes de que pueda encriptarse, debe crearse hasta un tamaño de bloque de 64 bits. Esto se hace con relleno, lo que implica agregar información adicional a un bloque para completarlo. Esto se puede hacer con varios esquemas diferentes, y también puede servir para hacer que la información cifrada sea más difícil de descifrar, pero no abordaremos eso en este artículo.

El horario clave de DES

Los algoritmos de cifrado usan claves para agregar datos que alterarán el resultado final del proceso. Si DES solo involucraba pasos como permutación y cajas S (la permutación se explica a continuación, mientras que las cajas S están cubiertas en Sustitución sección), todo lo que un atacante tendría que hacer es descubrir los detalles del algoritmo, luego hacer cada uno de los pasos a la inversa para revelar el mensaje inicial.

Dado que la mayoría de nuestros algoritmos son ampliamente conocidos, esto realmente no agregaría mucha seguridad. En cambio, las claves secretas se agregan para alterar la salida de una manera que no se puede predecir con solo conocer el algoritmo (siempre que se utilice un algoritmo suficientemente complejo).

DES comienza con una sola tecla, que se utiliza para crear subclaves que se aplican en cada ronda. Esta es una clave de 64 bits, que tiene el mismo tamaño que nuestros bloques. Digamos que nuestra clave es:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Ahora, esta clave está en binario, que es la forma en que los datos se expresan cuando las computadoras los procesan. Cuando los humanos manejan llaves, normalmente aparecerán como una mezcla de personajes, algo así:

kj329nf982bc9wn1

En DES, el primer paso para derivar nuestras teclas redondas es permutar la tecla (moverla) de acuerdo con la siguiente tabla:

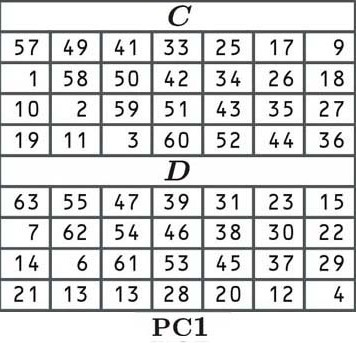
En la permutación, cada bit de nuestra clave original se baraja a una nueva posición como lo indica la tabla. Como la celda en la esquina superior izquierda (de C) dice 57, El primer número de nuestra clave permutada será el número en la posición 57 de nuestro antiguo bloque:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

La segunda celda dice 49, lo que significa que el segundo dígito de nuestra nueva clave será el número que está en la posición 49 de nuestro bloque anterior:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

La tercera celda dice 41, entonces buscamos el dígito en la posición 41:

01001010 10101101 11101000 10100101 01110001 0 01010100 10101001 1111010

Hasta ahora, nuestra clave está compuesta de “110“.

El resto de la clave se organiza de la misma manera, de acuerdo con los valores de la tabla. Nos movemos de izquierda a derecha, y una vez que llegamos al final de una fila, saltamos a la siguiente, como de costumbre. Una vez tabla C está terminado, saltamos a tabla D para completar la segunda mitad de la clave.

No hay una manera fácil de transponer todo nuestro bloque de acuerdo con la tabla de permutación inicial. Podrías hacer todo manualmente, o escribir un guión para ello (o incluso tener suerte y encontrar uno en las profundidades de Internet), pero vamos a hacer trampa y inventarlo:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

Puede que le preocupe que estemos inventando algunos de los números en esta guía, pero la realidad es que realmente no importa. Ya nadie cifra los datos manualmente, todo se hace a través de programas. El aspecto más crítico de este tutorial es que tiene una idea clara de los conceptos que estamos tratando. Los números en sí solo sirven para ayudarlo a visualizar lo que está sucediendo.

Algunos lectores pueden haber notado que la tabla (y ahora nuestra clave) solo tiene 56 bits en lugar de 64. Esto se debe a que se omite cada octavo bit. Este es un artefacto de los viejos tiempos de la tecnología, cuando era importante tener bits de verificación de paridad, que verificaban si la clave se había recibido correctamente. Estos bits de verificación de paridad significan que, en la práctica, DES solo tiene la seguridad de una clave de 56 bits.

Las tablas C y D nos dan una clave que tiene dos mitades de 28 bits. A veces, las mitades se denominan C y D, pero a lo largo de este artículo nos referiremos a ellas como L y R, para izquierda y derecha. Nuestro lado izquierdo es:

1100010 1010010 1010101 0101010

Si bien nuestro derecho es:

1010000 1111001 0001011 1000111

El siguiente paso es cambiar la tecla uno o dos espacios a la izquierda, dependiendo de la ronda. El número exacto de espacios se decide según la siguiente tabla predeterminada:

Número redondo Número de desplazamientos a la izquierda

1	1
2	1
3	2
4 4	2
5 5	2
6 6	2
7 7	2
8	2
9 9	1
10	2
11	2
12	2
13	2
14	2
15	2
dieciséis	1

Así que tomemos nuestras mitades izquierda y derecha:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

Y desplazarlos a ambos una posición hacia la izquierda, ya que la primera ronda tiene un desplazamiento de 1 de acuerdo con la tabla (el número en el extremo izquierdo se mueve al extremo derecho).

Subclave de primera ronda:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

En la segunda ronda, la tabla también dice 1, entonces este resultado será alterado nuevamente moviendo cada posición número uno a la izquierda.

Segunda ronda sub-clave:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

En la tercera ronda, los números se moverán dos lugares a la izquierda, porque la tabla ahora dice 2.

Subclave de la tercera ronda:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

En las rondas posteriores, los números se mueven hacia la izquierda de acuerdo con las distancias especificadas en la tabla, y cada turno se aplica al resultado de la ronda anterior. Al final, esto nos da dieciséis subclaves diferentes, una para cada ronda del proceso DES.

El siguiente paso es otra permutación de acuerdo con la tabla PC2 que se muestra a continuación:

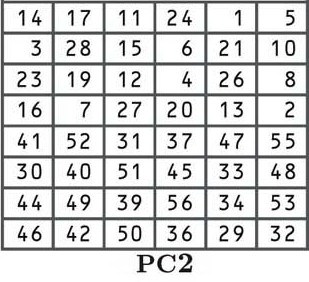
A estas alturas, debería estar familiarizado con las permutaciones, por lo que no entraremos en el proceso en profundidad. Si desea ver cómo funciona con más detalle, consulte la explicación cerca del comienzo de esta sección. Aunque las posiciones de reubicación son diferentes, el proceso es el mismo.

Cada una de las 16 teclas derivadas en el proceso de cambio ahora se baraja de acuerdo con la tabla, con el número de la posición 14 movido al primer lugar, el 17 al segundo, el 11 al tercero, etc…

Si observa detenidamente la tabla, notará que solo hay 48 bits, en lugar de los 56 bits que teníamos anteriormente. Este proceso se conoce como permutación de compresión..

También puede ver que la mitad superior de la tabla presenta números entre uno y 28, mientras que la mitad inferior contiene números del 29 al 56. Esto mantiene separadas las mitades izquierda y derecha de nuestras subclaves, y el espacio más grande lo indica a continuación en medio de las llaves.

Nuevamente, vamos a hacer trampa y a inventar los números. Digamos que todo este proceso nos dio las siguientes subclaves:

Ronda uno:         010101 010101 101010 110100 101001 100101 101010 101010

Segundo round:         011010 110101 101110 110010 010100 110010 111101 101101

Tercera ronda:     010100 100110 110110 101010 100110 011000 101011 011001

Cuarta ronda:         011001 110101 011001 110101 000011 001011 010101 010101

Quinta ronda:         110101 001101 010101 010101 010011 001011 010111 100101

Ronda seis:           010111 110101 011001 111001 101001 100101 101010 101010

Séptima ronda:     110101 111010 101110 101010 100110 010110 111011 001110

Octava ronda:       011001 110101 010101 001001 010011 001011 010100 101010

Ronda nueve:         111011 011010 011110 100010 100010 010110 110011 110010

Ronda 10:             011010 010101 101110 101001 010010 010110 111000 101010

Ronda 11:             110101 001101 101110 101010 100101 100101 101010 001010

Ronda 12:             101001 100100 101001 101010 100110 011000 101011 011001

Ronda 13:             010010 010010 010101 010101 010110 110001 100101 101010

Ronda 14:             101001 100110 010101 011101 010001 001010 110010 111110

Ronda 15:             011001 011010 011001 110101 001001 011001 100101 101101

Ronda 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Este proceso de desplazamiento da como resultado que cada bit de la clave inicial se use en aproximadamente 14 de las 16 subclaves, aunque algunos bits se usan un poco más que otros.

Permutación inicial

Una vez que los datos se hayan dividido en bloques y se hayan rellenado si es necesario, es hora de comenzar el proceso de cifrado DES. Volveremos a las subclaves que acabamos de crear en una etapa posterior. El primer paso se conoce como la permutación inicial, donde los datos se reorganizan de acuerdo con la siguiente tabla:

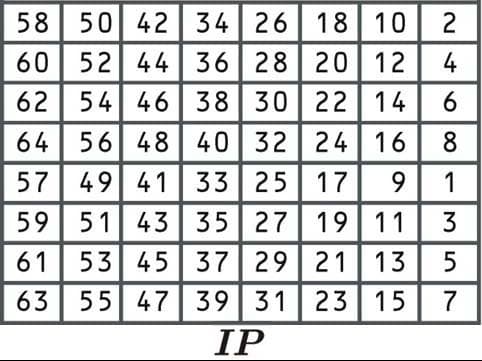
Este proceso de permutación inicial no hace que el algoritmo sea más seguro. Esto se debe a que no implica la entrada de ninguna clave y puede revertirse fácilmente. El algoritmo se diseñó originalmente de esta manera porque facilitaba la implementación en ciertos contextos..

Como hemos cubierto las permutaciones un par de veces, omitiremos cualquier explicación importante aquí. Regresar a El horario clave de DES sección si necesita más información sobre cómo funcionan.

Tomemos el primer bloque del mensaje “Vamos a la playa”, que derivamos en el Bloquear sección bajo Comprender el algoritmo DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Como la primera celda dice 58, seleccionaríamos el número de la posición 58:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Luego tomaríamos el número de la posición 50:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Y el número de la posición 42:

01001100 01100101 01110100 00100111 01110011 00 0100000 01100111 01101111

Esto nos da “110” hasta aquí. Haremos el resto del número:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Cuando se completa la permutación inicial, los datos pasan al siguiente paso.

Dividiendo los bloques

Una vez que los datos han sufrido su permutación inicial, se dividen en dos mitades. Tomamos nuestro bloque que acaba de sufrir su permutación inicial:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Y lo separaremos en dos bloques, un bloque izquierdo (formado por los primeros 32 dígitos), conocido como L0 0:

L0 0    11010111 01001010 10101000 10011101

Y un bloque derecho (compuesto por los segundos 32 dígitos), conocido como R0 0:

R0 0    01001011 10110101 10000111 10101001

La función F

Ahora que el bloque se ha dividido, es hora de que tenga lugar la función F. En la primera ronda, solo se aplicará a la mitad derecha del bloque, mientras que la mitad izquierda se mantiene a un lado hasta más tarde. El lado derecho se somete a los siguientes cuatro pasos como parte de la función F:

• Permutación de expansión (E en el diagrama)
• Mezcla de teclas (⊕ en el diagrama)
• Sustitución (cada S1, S2, etc. en el diagrama)
• Permutación (P en el diagrama)

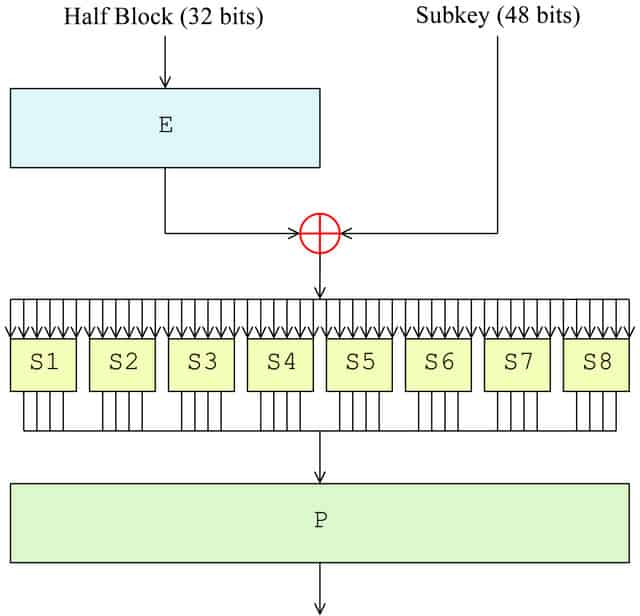
Permutación de expansión

La permutación de expansión logra tres cosas. Lo más importante es que permite que bits individuales de datos de entrada afecten la salida de otros dos bits, causando un efecto de avalancha. También genera la mitad derecha de 48 bits, de modo que tiene el mismo tamaño que la subclave para el siguiente paso. El otro efecto de la permutación de expansión es que hace que la salida sea más larga que la entrada. Esto permite que se comprima en la operación de sustitución..

Los bits se reorganizan de acuerdo con la siguiente tabla. Algunos de los bits individuales están en la tabla dos veces, que es cómo el bloque se expandió de 32 a 48 bits:

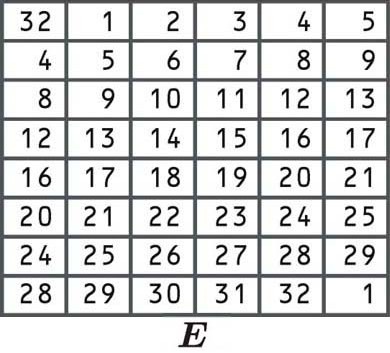
Como la primera celda dice 32, tomamos nuestro bloque derecho y seleccionamos el número de la posición 32, tal como lo hicimos en los otros ejemplos de permutación enumerados anteriormente:

R0 0    01001011 10110101 10000111 10101001

Luego tomamos los números desde la primera posición, la segunda posición y así sucesivamente, hasta llegar a la esquina inferior derecha del bloque. Ya que hay un 1 en esta celda, el último dígito también será el número que aparece en la primera posición de nuestro bloque.

Digamos que la permutación de expansión nos da un nuevo bloque de 48 bits de:

101110 100110 100100 000000 001100 001110 101101 011110

Mezcla de teclas

Una vez que el bloque se ha expandido a 48 bits, es hora de aplicar la subclave de la primera ronda, que derivamos en Horario clave de DES sección de arriba. La subclave modifica el bloque mediante el cifrado XOR.

El cifrado XOR es un cifrado adicional que sigue un proceso simple, especialmente cuando se compara con los otros elementos que ya hemos discutido.

En un cifrado XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Entonces, digamos que tienes que XOR los siguientes dos números en binario:

1101

0101

Cada dígito se agregaría al que está debajo. De acuerdo con las tres reglas que se muestran arriba, esto da un resultado de:

1000

Para completar el paso de mezcla de teclas, tomamos el lado derecho de nuestro bloque que acabamos de expandir a 48 bits, y la primera tecla redonda. Luego realizamos la adición XOR:

Bloquear:                      101110 100110 100100 000000 001100 001110 101101 011110

Clave redonda:     010101 010101 101010 110100 101001 100101 101010 101010

Resultado XOR:             111011 110011 001110 110100 100101 101011 000111 110100

El resultado de la operación XOR se pasa a la siguiente ronda..

Sustitución

La sustitución agrega confusión a los datos. Normalmente se realiza con tablas de búsqueda, que también se conocen como cuadros de sustitución o cuadros S. DES utiliza ocho tablas separadas o cajas S, una diferente para cada 6 bits de datos. La siguiente tabla muestra los ocho S-boxes de DES:

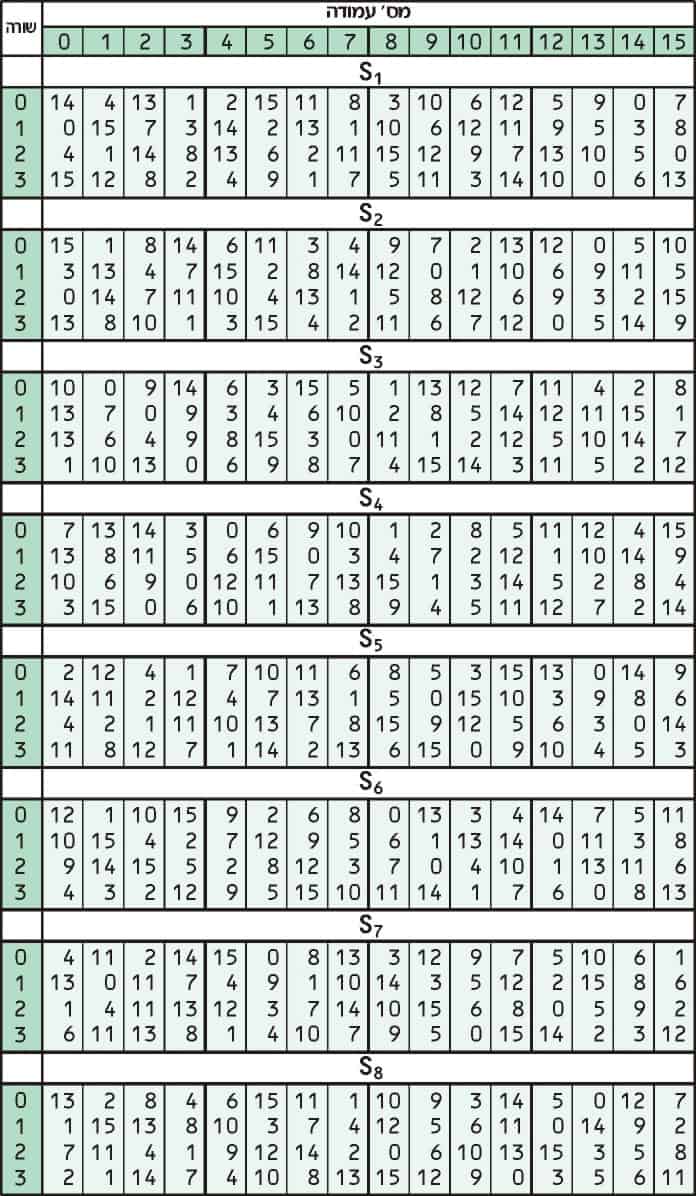
Las ocho cajas S separadas se utilizan para traducir cada entrada de 6 bits en una salida de 4 bits. El primer paso en el proceso es tomar los dígitos al principio y al final de un segmento de 6 bits, luego convertir ese valor binario a decimal.

Tomemos los datos que acabamos de terminar de XOR en el paso anterior:

111011 110011 001110 110100 100101 101011 000111 110100

Veremos el primer segmento de 6 bits para mostrarle cómo funciona el proceso de sustitución:

111011

Dado que el primer número y el último número son ambos 1, esto nos da un valor de 11. Luego convertimos 11 de binario a decimal, lo que nos da 3. Estos son solo valores equivalentes, escritos de diferentes maneras. Piense en ello como la conversión del lenguaje informático al lenguaje humano. Puede verificar la conversión usted mismo con una calculadora en línea si lo desea.

Luego tomamos los cuatro dígitos del medio del primer segmento de 6 bits:

111011

Y convertirlos de binario a decimal. 1101 se traduce al número 13.

Ahora, tomamos estos dos números y los buscamos en el S1 mesa:

               

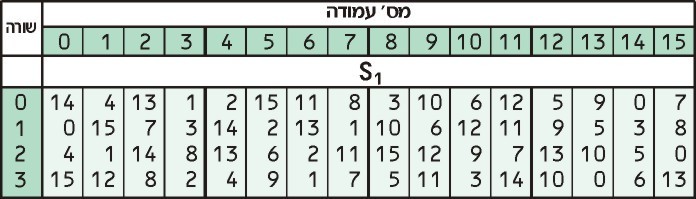
Nuestro primer numero, 3, nos dice que miremos en la tercera fila, mientras que nuestro segundo número, 13 nos dice que miremos en la 13a columna. El valor en la tercera fila de la 13a columna es 0 0.

Ahora que hemos buscado nuestro número en la tabla, lo convertimos nuevamente a binario de cuatro dígitos. Cero normalmente se escribe como 0 en binario, pero 0000 es el mismo, y este es el formato más adecuado para nuestros propósitos.

Siguiendo este proceso, el S-box convierte nuestra primera sección de datos de 6 bits (111011) en un valor diferente de 4 bits (0000) Parece complicado, pero esta técnica ayuda a oscurecer aún más la relación entre el texto cifrado y el texto sin formato al que está vinculado.

La siguiente sección de datos de 6 bits pasa por el mismo proceso, pero en su lugar utiliza el cuadro S2 que se muestra arriba. La tercera sección usa la tabla S3 y así sucesivamente, hasta que la sección final sufre la sustitución a través de la tabla S8.

Nuevamente, vamos a hacer trampa para el resto de los valores. Digamos que los cuadros de sustitución nos dan un resultado de:

0000 1010 1100 1001 0100 1001 0111 0001

Una vez que cada sección de los datos ha pasado por su S-box, pasa al siguiente paso.

Permutación

La última etapa de la función F es otra permutación, utilizando la siguiente tabla: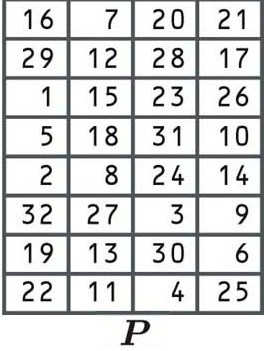

En este momento, debe tener una comprensión decente de cómo las permutaciones cambian los dígitos del bloque anterior a una posición diferente en el bloque nuevo, por lo que no volveremos a entrar en él nuevamente.

Digamos que esta permutación toma nuestro resultado anterior:

0000 1010 1100 1001 0100 1001 0111 0001

Y nos da una salida de:

0101 0110 1001 0101 0010 0100 0101 0010

Ahora que se ha completado la permutación, hemos terminado con los cuatro pasos de la función F en esta ronda. En notación matemática, este valor se conoce como f (R0 0, K1). Esto significa que el resultado es la función (F) del lado derecho inicial del bloque (R0) y la subclave de la primera ronda (K1).

XOR con el bloque izquierdo

¿Recuerdas cómo dividimos el bloque por la mitad justo antes de comenzar los pasos de la función F? Dejamos a un lado el lado izquierdo del bloque (L0), mientras que el lado derecho se sometió a cada uno de estos procesos. Bueno, ahora es el momento de que L0 vuelva a la acción.

Tomamos el lado correcto que acabamos de procesar f (R0 0, K1) y agréguelo al lado izquierdo anterior (L0 0) utilizando el cifrado XOR. Esto nos da R1, El resultado de nuestra primera ronda:

f (R0 0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0 0:                                    1101 0111 0100 1010 1010 1000 1001 1101

Resultado XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Referirse a Mezcla de teclas sección anterior si necesita un recordatorio de cómo funciona el cifrado XOR.

15 rondas más …

Si has llegado hasta aquí, entonces DES probablemente parezca un proceso arduo. Pero aún no está cerca de estar terminado. Los datos pasan por los cuatro pasos de la función F, seguidos por el XOR, otras 15 veces, para un total de 16 rondas..

En la segunda ronda, tomamos la versión original intacta del lado derecho del bloque (R0) y lo convertimos en el nuevo lado izquierdo (L1). Mientras tanto, tomamos el resultado de nuestra primera ronda y lo enviamos a través de la función F. Todo sucede igual que la última vez, sin embargo, esta vez se usa la subclave para la segunda ronda. Digamos que este proceso nos da un resultado de:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Luego XOR el resultado con L1, que en realidad es R0 (derivamos esto en el Dividiendo bloques sección). Esto nos da el resultado de la segunda ronda, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Este paso puede parecer un poco confuso, pero bajo el esquema Feistel, el viejo lado derecho se convierte en el nuevo izquierdo, mientras que el resultado de la operación se convierte en el nuevo lado derecho.

El siguiente diagrama le ofrece una representación visual de lo que está sucediendo. IP representa la permutación inicial, F es un sustituto de toda la función F, ⊕ simboliza la función XOR y las flechas indican que cada lado del bloque se mueve entre izquierda y derecha:

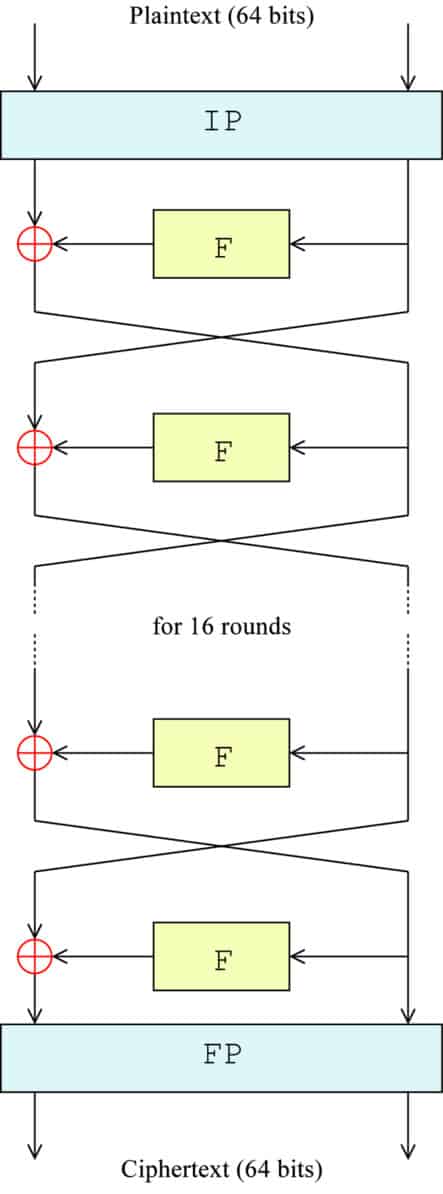
La fórmula exacta para cada paso es:

Lnorte = Rn-1

Rnorte = Ln-1 + F(Rn-1,Knorte)

Dónde:

L = La mitad izquierda del bloque (comenzando con L0 cuando el bloque se dividió inicialmente)

R = La mitad derecha del bloque (comenzando con R0 cuando el bloque se dividió inicialmente)

n = El número redondo (comenzando con 0, cuando el bloque se dividió inicialmente)

f = La función F

Kn = La subclave para la ronda n

De acuerdo con la fórmula y el diagrama, en la tercera ronda, R1 se convierte en la nueva mitad izquierda (L2), mientras que R2 se procesa a través de la función F. Digamos que nos da un resultado de:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Luego calculamos el resultado de nuestra tercera ronda (R3), utilizando el cifrado XOR, como antes:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

El mismo proceso continúa hasta la decimoquinta ronda, con los bloques cambiando y la siguiente subclave se usa en cada ronda. En la ronda 16 y final, los bloques no se cambian. En cambio, se combinan para formar un bloque de 64 bits. Abstenerse de intercambiar los bloques en esta última etapa permite que el algoritmo se use tanto para el cifrado como para el descifrado.

Digamos que la ronda final nos da un resultado de:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Permutación final

Esta permutación es la inversa de la permutación inicial y, de nuevo, no agrega ningún valor de seguridad adicional. Reorganiza los datos de acuerdo con la siguiente tabla:

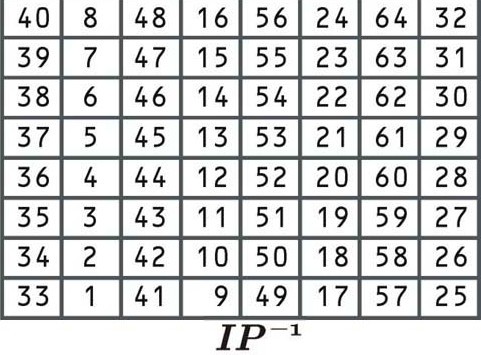
Esta tabla de permutación funciona igual que las anteriores. Dado que es el paso final del proceso de cifrado, el resultado será el texto cifrado para el primer bloque de “Vamonos a la playa”. Digamos que el bloque encriptado es:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Ahora, si quisieras el texto cifrado real para “Vamos a la playa”, podrías haber omitido todo el proceso de aprendizaje y pasar directamente a una herramienta de cifrado DES en línea. Si ingresamos nuestra oración junto a una clave (digamos kj329nf982bc9wn1) la herramienta nos da un texto cifrado de:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Si lo desea, puede convertir la clave y el texto cifrado a binario y luego comparar cómo texto cifrado del primer bloque se alinea con todo el proceso que se ha esbozado.

Descifrado DES

En DES, el proceso de descifrado es increíblemente sencillo. La estructura Feistel del algoritmo le permite revertirse fácilmente. El proceso se ejecuta casi exactamente igual para descifrar la información. La única diferencia es que las subclaves se aplican a la inversa. Esta es una configuración eficiente, porque significa que se puede usar el mismo software y hardware en los procesos de cifrado y descifrado..

Para descifrar los datos, primero pasa por una permutación inicial, luego el bloque se divide y la mitad derecha pasa por la función F. La diferencia es que en la primera ronda de descifrado, se aplica la 16ª subclave. Todo lo demás procede de manera normal. Una vez que se completa la función F, se XOR con el lado izquierdo del bloque.

Los bloques se cambian y el resultado pasa por el mismo proceso para la segunda ronda, con la única excepción de que se aplica la 15ª subclave. Este proceso continúa hasta la 16ª ronda, cuando se usa la primera subclave.

Al igual que en el proceso de cifrado, los bloques no se intercambian en la etapa final, y luego los datos se someten a una permutación final. Esto finaliza el proceso de descifrado, lo que da como resultado el texto sin formato original del mensaje..

3DES

A medida que las debilidades de seguridad de DES se hicieron más evidentes, 3DES se propuso como una forma de extender su tamaño de clave sin tener que construir un algoritmo completamente nuevo. En lugar de utilizar una sola clave como en DES, 3DES ejecuta el algoritmo DES tres veces, con tres claves de 56 bits:

• La clave uno está acostumbrada a encriptar el texto sin formato.
• La clave dos se usa para descifrar el texto que había sido encriptado por la clave uno.
• La clave tres se usa para encriptar el texto que fue descifrado por la clave tres.

En cada etapa, se sigue el proceso completo de DES como se describe anteriormente.

Ahora, se estará preguntando “¿Cómo puede mejorar la seguridad la aplicación de descifrado en el segundo paso?”

La respuesta es que usa una clave separada. Si la primera clave también se usó para descifrar los datos en el segundo paso, entonces los datos volverían a donde comenzaron.

Sin embargo, dado que utiliza una clave diferente, el proceso de descifrado en realidad no sirve para descifrar los datos. Puede parecer lógicamente perverso, pero descifrar con una clave separada solo sirve para mezclar aún más los datos.

Una vez que la segunda clave ha “descifrado” los datos, la tercera clave se aplica para cifrarlos nuevamente. El resultado es el texto cifrado 3DES.

3DES está estructurado de esta manera porque permite que las implementaciones sean compatibles con DES de una sola tecla, DES de dos teclas y DES de tres teclas (se tratan en la siguiente sección). Esto no funcionaría si se usara el cifrado en los tres pasos.

Opciones de codificación 3DES

Técnicamente, 3DES se puede implementar con tres configuraciones clave diferentes. A pesar de esto, la segunda y tercera opción son inseguras y nunca deben implementarse.

• Opción de codificación uno – Esta opción utiliza tres teclas independientes y es la más segura..
• Opción de incrustación dos – En esta configuración, la primera y la tercera clave son las mismas.
• Opción de clave tres – Esto usa tres claves idénticas. Cuando se usan claves idénticas, el proceso de descifrado en la segunda etapa cancela el primer cifrado, dejando solo el cifrado final para alterar los datos. Esto hace que el resultado sea igual que el DES ordinario.

El proceso 3DES: Clave opción uno

Seamos honestos, la totalidad del proceso 3DES puede hacer que su cabeza gire, especialmente si es nuevo en la criptografía. Para ayudarlo a asimilar, aquí hay un breve resumen del esquema de cifrado completo del algoritmo 3DES:

El texto sin formato ingresa al algoritmo 3DES y es el primero cifrado con la clave uno en los siguientes pasos:

• • Programa clave: las 16 subclaves se derivan de la clave uno

  • Permutación inicial

  • El bloque se divide en mitades izquierda y derecha.

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la ronda

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Convierta el viejo lado derecho en el nuevo lado izquierdo, y el resultado en el nuevo lado derecho

      Repita los pasos anteriores 14 veces

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la 16ª ronda

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Combina los lados izquierdo y derecho del bloque

• • Permutación final

Tome el texto que se ha cifrado con la clave uno y luego envíelo a través de Proceso de “descifrado” con llave dos:

• • Programa clave: las 16 subclaves se derivan de la clave dos

  • Permutación inicial

  • El bloque se divide en mitades izquierda y derecha.

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la ronda (a partir de la 16 subclave para descifrar)

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Convierta el viejo lado derecho en el nuevo lado izquierdo, y el resultado en el nuevo lado derecho

      Repita los pasos anteriores 14 veces

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la primera ronda

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Combina los lados izquierdo y derecho del bloque
  • Permutación final

Tome los datos que han sido “descifrados” por la clave dos, luego envíelos a través del enproceso de cifrado con llave Tres:

• • Programa clave: las 16 subclaves se derivan de la clave tres

  • Permutación inicial

  • El bloque se divide en mitades izquierda y derecha.

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la ronda

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Convierta el viejo lado derecho en el nuevo lado izquierdo, y el resultado en el nuevo lado derecho

      Repita los pasos anteriores 14 veces

• • • La mitad derecha se envía a través de la función F

      • Permutación de expansión

      • XOR con la subclave para la 16ª ronda

      • Sustitución

      • Permutación

    • XOR el resultado de la función F con el lado izquierdo

    • Combina los lados izquierdo y derecho del bloque

• • Permutación final

El resultado es el texto cifrado 3DES.

La seguridad de 3DES

La seguridad de 3DES depende de la opción de codificación que se esté utilizando. La opción de codificación uno involucra tres claves diferentes de 56 bits, lo que le da una longitud total de clave de 168 bits. La longitud efectiva se reduce considerablemente mediante ataques de encuentro en el medio, que reducen su seguridad en el mundo real a 112 bits..

Los ataques Meet-in-the-middle son útiles contra esquemas de cifrado que repiten el mismo algoritmo varias veces. La técnica almacena los valores inmediatos de cada etapa de encriptación, luego usa esta información para mejorar radicalmente el tiempo que tomaría la fuerza bruta del algoritmo.

Las opciones dos y tres tienen teclas significativamente más pequeñas y son vulnerables a los ataques de texto plano conocido y de texto plano elegido, así como a otros..

Los ataques conocidos de texto sin formato son posibles cuando un adversario tiene acceso tanto al texto sin formato como al texto cifrado de un mensaje. Si un algoritmo es susceptible a estos ataques, el atacante puede usar esta información para deducir la clave, lo que le permite descifrar todos los demás datos que han sido cifrados por la misma clave.

Un ataque de texto sin formato elegido es similar, pero implica que el atacante descubra la clave comparando textos cifrados con textos claros arbitrarios.

Debido a estas vulnerabilidades y al tamaño general de las claves pequeñas involucradas, las opciones de codificación dos y tres son inseguras y no deben implementarse.

¿Es seguro 3DES??

Dado que 3DES quedará en desuso en los próximos años, es mejor usar otros algoritmos. Si bien la opción de codificación uno todavía se considera segura para muchas aplicaciones, no hay muchas buenas razones por las que debería usarse en lugar de una alternativa como AES.

Aunque 3DES ocupa un lugar importante en la criptografía como seguimiento de DES, sus años de gloria han terminado y es hora de seguir adelante. Si desea asegurar sus sistemas en el futuro, debería utilizar un algoritmo más actualizado..

Relacionado: Tipos de cifrado comunes explicados

Plan X por DoD con licencia bajo CC0