O que é criptografia RSA e como funciona?

A criptografia RSA é um sistema que resolve o que antes era um dos maiores problemas em criptografia: Como você pode enviar a alguém uma mensagem codificada sem ter a oportunidade de compartilhar o código anteriormente com eles?

Este artigo ensinará tudo o que você precisa saber sobre como a criptografia RSA foi desenvolvida, como funciona, a matemática por trás disso, para que é usado bem como alguns dos maiores problemas de segurança que enfrenta. Aprender sobre a RSA fornecerá um conhecimento básico que ajuda você a entender quantas partes da nossa vida on-line são mantidas em segurança.

O que é criptografia RSA?

Digamos que você queira contar a seu amigo um segredo. Se você está ao lado deles, pode apenas sussurrar. Se você estiver em lados opostos do país, isso obviamente não funcionará. Você pode anotá-lo e enviá-lo por correio ou usar o telefone, mas cada um desses canais de comunicação é inseguro e qualquer pessoa com uma motivação suficientemente forte poderia facilmente interceptar a mensagem.

Se o segredo fosse importante o suficiente, você não correria o risco de escrevê-lo normalmente – espiões ou um funcionário postal desonesto pode estar olhando por seu correio. Da mesma forma, alguém pode estar tocando no seu telefone sem o seu conhecimento e registrando todas as chamadas que você faz.

Uma solução para impedir que os bisbilhoteiros acessem o conteúdo da mensagem é: criptografar. Isso basicamente significa adicionar um código à mensagem que o transforma em uma bagunça confusa. Se o seu código for suficientemente complexo, as únicas pessoas que poderão acessar a mensagem original são aquelas que terão acesso ao código.

Se você teve a chance de compartilhar o código com seu amigo antes, qualquer um de vocês pode enviar uma mensagem criptografada a qualquer momento, sabendo que vocês dois são os únicos com a capacidade de ler o conteúdo da mensagem. Mas e se você não tivesse a chance de compartilhar o código antecipadamente?

Esse é um dos problemas fundamentais da criptografia, que foi abordado por esquemas de criptografia de chave pública (também conhecidos como criptografia assimétrica) como RSA.

Sob a criptografia RSA, as mensagens são criptografadas com um código chamado chave pública, que pode ser compartilhado abertamente. Devido a algumas propriedades matemáticas distintas do algoritmo RSA, depois que uma mensagem é criptografada com a chave pública, ela só pode ser descriptografada por outra chave, conhecida como chave privada. Cada usuário do RSA possui um par de chaves que consiste em suas chaves públicas e privadas. Como o nome sugere, a chave privada deve ser mantida em segredo.

Os esquemas de criptografia de chave pública diferem dos criptografia de chave simétrica, em que o processo de criptografia e descriptografia usa a mesma chave privada. Essas diferenças tornam a criptografia de chave pública como o RSA útil para a comunicação em situações nas quais não houve oportunidade de distribuir as chaves com segurança de antemão..

Os algoritmos de chave simétrica têm seus próprios aplicativos, como criptografar dados para uso pessoal ou quando existem canais seguros nos quais as chaves privadas podem ser compartilhadas.

Veja também: Criptografia de chave pública

Onde a criptografia RSA é usada?

A criptografia RSA é frequentemente usada em combinação com outros esquemas de criptografia, ou para assinaturas digitais o que pode provar a autenticidade e integridade de uma mensagem. Geralmente, não é usado para criptografar mensagens ou arquivos inteiros, porque é menos eficiente e consome mais recursos do que a criptografia de chave simétrica.

Para tornar as coisas mais eficientes, um arquivo geralmente será criptografado com um algoritmo de chave simétrica e, em seguida, a chave simétrica será criptografada com criptografia RSA. Nesse processo, apenas uma entidade que tenha acesso à chave privada RSA poderá descriptografar a chave simétrica.

Sem poder acessar a chave simétrica, o o arquivo original não pode ser descriptografado. Este método pode ser usado para manter mensagens e arquivos seguros, sem demorar muito ou consumir muitos recursos computacionais.

A criptografia RSA pode ser usada em vários sistemas diferentes. Ele pode ser implementado no OpenSSL, wolfCrypt, cryptlib e várias outras bibliotecas criptográficas.

Como um dos primeiros esquemas de criptografia de chave pública amplamente utilizados, a RSA lançou as bases para grande parte de nossas comunicações seguras. isso foi tradicionalmente usado em TLS e também foi o algoritmo original usado na criptografia PGP. O RSA ainda é visto em vários navegadores, email, VPNs, bate-papo e outros canais de comunicação.

O RSA também é frequentemente usado para fazer conexões seguras entre clientes e servidores VPN. Sob protocolos como o OpenVPN, os handshakes TLS podem usar o algoritmo RSA para trocar chaves e estabelecer um canal seguro.

O plano de fundo da criptografia RSA

Como mencionamos no início deste artigo, antes da criptografia de chave pública, era um desafio se comunicar com segurança se não houvesse a chance de trocar chaves com segurança de antemão. Se não houvesse a oportunidade de compartilhar o código antecipadamente, ou um canal seguro através do qual as chaves pudessem ser distribuídas, não havia como se comunicar sem a ameaça de os inimigos serem capazes de interceptar e acessar o conteúdo da mensagem.

Não foi até a década de 1970 que as coisas realmente começaram a mudar. O primeiro grande desenvolvimento em direção ao que chamamos agora de criptografia de chave pública foi publicado no início da década por James H. Ellis. Ellis não conseguiu encontrar uma maneira de implementar seu trabalho, mas foi expandido por seu colega Clifford Cocks para se tornar o que hoje conhecemos como Criptografia RSA.

A peça final do quebra-cabeça é o que chamamos agora de Troca de chaves Diffie-Hellman. Malcolm J. Williamson, outro colega de trabalho, descobriu um esquema que permitia que duas partes compartilhassem uma chave de criptografia, mesmo que o canal estivesse sendo monitorado por adversários..

Todo esse trabalho foi realizado na agência de inteligência do Reino Unido, o Government Communications Headquarters (GCHQ), que manteve a descoberta classificada. Em parte devido a limitações tecnológicas, o GCHQ não conseguia ver o uso da criptografia de chave pública na época, então o desenvolvimento ficou ocioso na prateleira, acumulando poeira. Não foi até 1997 que o trabalho foi desclassificado e os inventores originais da RSA foram reconhecidos.

Vários anos depois, conceitos semelhantes começaram a se desenvolver na esfera pública. Ralph Merkle criou uma forma inicial de criptografia de chave pública, que influenciou Whitfield Diffie e Martin Hellman no design da troca de chaves Diffie-Hellman.

As idéias de Diffie e Hellman estavam faltando em um aspecto importante que tornaria seu trabalho uma base de criptografia de chave pública. Este foi um função unidirecional que seria difícil de inverter. Em 1977, Ron Rivest, Adi Shamir e Leonard Adleman, cujos sobrenomes formam a sigla RSA, surgiram com uma solução após um ano trabalhando no problema.

Os acadêmicos do MIT fizeram o seu avanço após uma festa da Páscoa em 1977. Depois de uma noite bebendo, Rivest foi para casa, mas em vez de dormir, ele passou a noite escrevendo febrilmente um papel que formalizou sua idéia para a necessária função unidirecional..

A idéia foi patenteada em 1983 pelo MIT, mas não foi até os primeiros dias da Internet que o algoritmo RSA começou a ver a adoção generalizada como uma importante ferramenta de segurança.

Como a criptografia RSA funciona?

A seguir, será um pouco de simplificação, porque muitos leitores provavelmente foram assustados pelo professor de matemática do ensino médio. Para evitar que a matemática fique fora de controle, estaremos simplificando alguns conceitos e usando números muito menores. Na realidade, a criptografia RSA usa números primos que são muito maiores em magnitude e existem algumas outras complexidades.

Existem vários conceitos diferentes que você terá que entender antes de podermos explicar como tudo se encaixa. Esses incluem funções de alçapão, gerando primos, a função totiente de Carmichael e os processos separados envolvidos na computando as chaves públicas e privadas usado nos processos de criptografia e descriptografia.

Funções da porta de interceptação

A criptografia RSA funciona sob a premissa de que o algoritmo é fácil de calcular em uma direção, mas quase impossível ao contrário. Por exemplo, se lhe dissessem que 701.111 é um produto de dois números primos, você seria capaz de descobrir quais são esses dois números?

Mesmo com uma calculadora ou um computador, a maioria de nós não tem idéia de por onde começar, e muito menos é capaz de descobrir a resposta. Mas se revirarmos as coisas, ficará muito mais fácil. Qual é o resultado de:

907 x 773

Se você estivesse entediado o suficiente, seria capaz de sacar seu telefone ou talvez calculá-lo em sua cabeça para descobrir que a resposta é a 701.111 mencionada anteriormente. Estes 907 e 773 são os números primos que respondem à nossa primeira pergunta, o que nos mostra que certas equações podem ser fáceis de descobrir de uma maneira, mas aparentemente impossíveis ao contrário..

Outro aspecto interessante dessa equação é que é simples descobrir um dos números primos se você já possui o outro, assim como o produto. Se você disser que 701.111 é o resultado de 907 multiplicado por outro número primo, você pode descobrir o outro primo com a seguinte equação:

701.111 ÷ 907 = 773

Como a relação entre esses números é simples de calcular em uma direção, mas incrivelmente difícil ao contrário, a equação é conhecida como função de alçapão. Esteja ciente de que, embora o exemplo acima seja difícil para as pessoas descobrirem, os computadores podem fazer a operação em um período trivial.

Por esse motivo, o RSA usa números muito maiores. O tamanho dos primos em uma implementação real do RSA varia, mas no RSA de 2048 bits, eles se uniam para criar chaves com 617 dígitos. Para ajudá-lo a visualizá-lo, uma chave seria um número deste tamanho:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Gerando números primos

As funções do alçapão mencionadas acima formam a base de como os esquemas de criptografia de chave pública e privada funcionam. Suas propriedades permitem que chaves públicas sejam compartilhadas sem pôr em risco a mensagem ou revelar a chave privada. Eles também permitem que os dados sejam criptografados com uma chave de uma maneira que só possa ser descriptografada pela outra chave do par.

A primeira etapa da criptografia de uma mensagem com o RSA é gerar as chaves. Para fazer isso, precisamos dois números primos (p e q) que são selecionados com um teste de primalidade. Um teste de primalidade é um algoritmo que encontra eficientemente números primos, como o teste de primalidade de Rabin-Miller.

Os números primos no RSA precisam ser muito grandes e também relativamente distantes. Números pequenos ou mais próximos são muito mais fáceis de decifrar. Apesar disso, nosso exemplo usará números menores para facilitar o acompanhamento e a computação.

Digamos que o teste de primalidade nos dê os números primos que usamos acima, 907 e 773. O próximo passo é descobrir o módulo (n), usando a seguinte fórmula:

n = p x q

Onde p = 907 e q = 773

Portanto:

n = 907 x 773

n = 701.111

Função totiente de Carmichael

Depois que tivermos n, nós usamos Função totiente de Carmichael:

    λ(n) = lcm (p – 1, q – 1)

Se já faz um tempo desde que você acessou os livros didáticos de matemática, as opções acima podem parecer um pouco assustadoras. Você pode pular esta parte e apenas confiar que a matemática funciona; caso contrário, fique conosco para mais alguns cálculos. Tudo será explicado com o máximo de detalhes possível para ajudá-lo a entender o básico.

Para quem não sabe, λ (n) representa o paciente de Carmichael para n, enquanto lcm significa o menor múltiplo comum, qual é o número mais baixo que ambos p e q pode dividir em. Existem algumas maneiras diferentes de descobrir isso, mas o mais fácil é confiar em uma calculadora on-line para fazer a equação para você. Então, vamos colocar nossos números na equação:

    λ(701.111) = lcm (907 – 1, 773 – 1)

    λ(701.111) = lcm (906, 772)

   Usando a calculadora vinculada acima, isso nos dá:

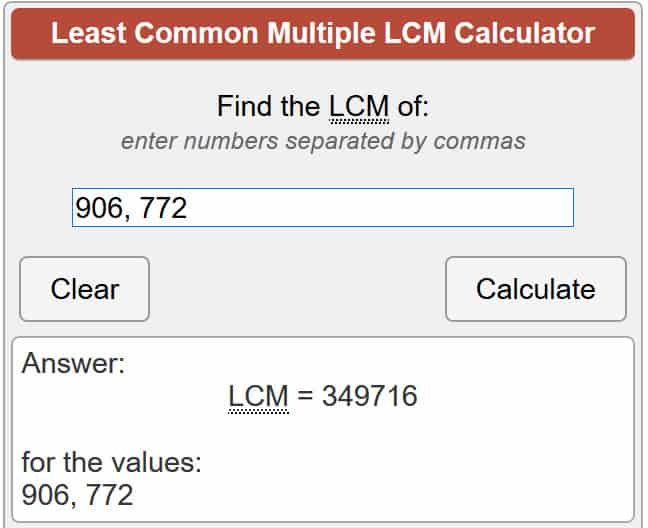
    λ(701.111) = 349.716

Gerando a chave pública

Agora que temos Carmichael atento aos nossos números primos, é hora de descobrir nossa chave pública. Sob RSA, chaves públicas são compostas por um número primo e, assim como n. O número e pode estar entre 1 e o valor de λ(n), que em nosso exemplo é 349.716.

Como a chave pública é compartilhada abertamente, não é tão importante para e para ser um número aleatório. Na prática, e é geralmente definido em 65.537, porque quando números muito maiores são escolhidos aleatoriamente, isso torna a criptografia muito menos eficiente. Para o exemplo de hoje, manteremos os números pequenos para tornar os cálculos eficientes. Digamos:

e = 11

Nossos dados criptografados finais são chamados de texto cifrado (c) Nós derivamos da nossa mensagem de texto simples (m), aplicando a chave pública com a seguinte fórmula:

c = me mod n

Já criamos e e nós sabemos n também. A única coisa que precisamos explicar é mod. Está um pouco fora da profundidade deste artigo, mas refere-se a um operação do módulo, o que significa essencialmente o restante que resta quando você divide um lado pelo outro. Por exemplo:

10 mod 3 = 1

Isso ocorre porque 3 entra em 10 três vezes, com um restante de 1.

De volta à nossa equação. Para simplificar, digamos que a mensagem (m) que queremos criptografar e manter em segredo é apenas um número, 4. Vamos conectar tudo:

c = me mod n

c = 411 mod 701.111

c = 4.194.304 mod 701.111

Mais uma vez, para fazer o operação do módulo fácil, usaremos uma calculadora on-line, mas você pode descobrir por si mesmo. Ao inserir 4.194.304 na calculadora on-line, ele nos fornece:

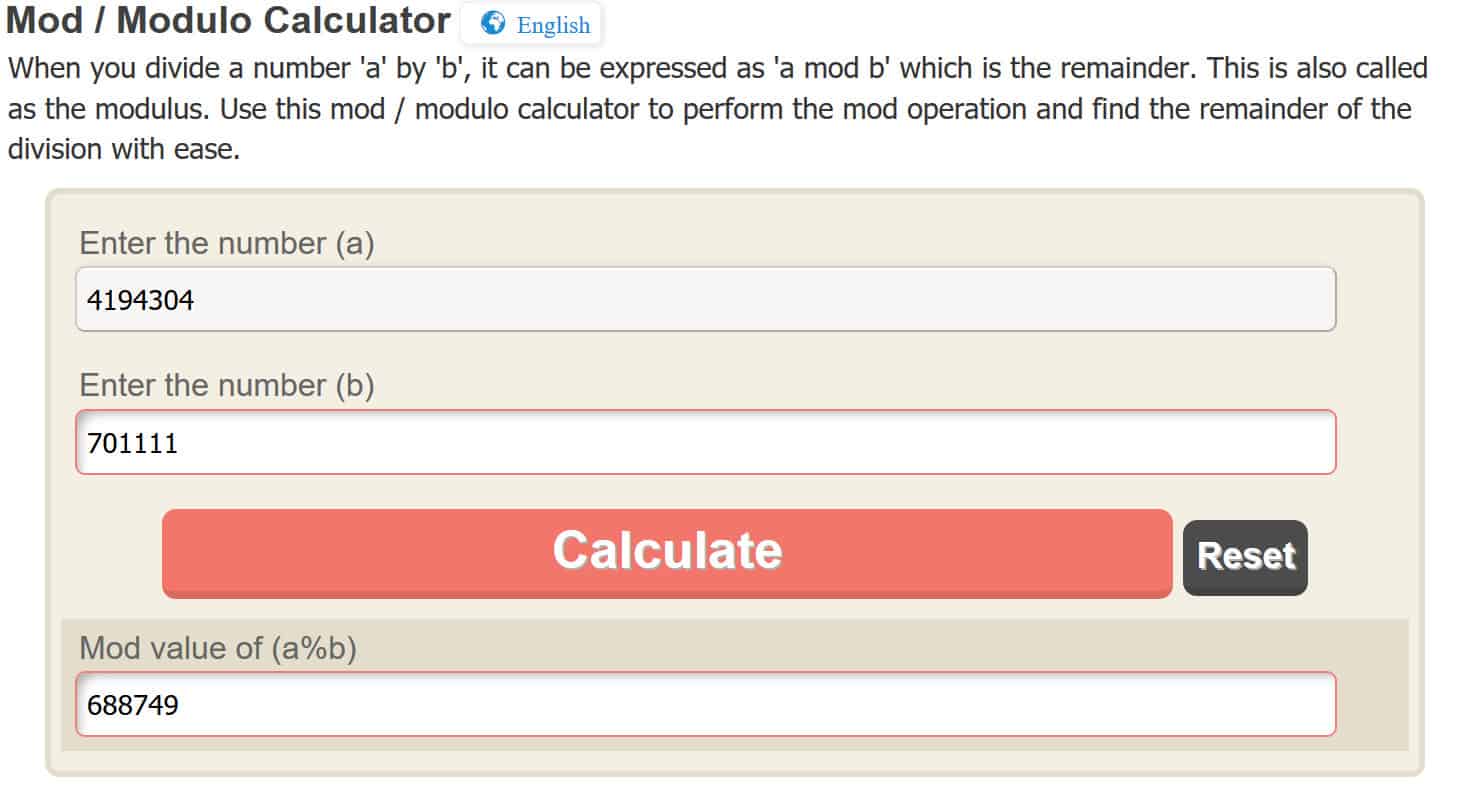
c = 688.749

Portanto, quando usamos o RSA para criptografar nossa mensagem, 4, com nossa chave pública, ela nos dá a texto cifrado de 688.749. As etapas anteriores podem parecer um pouco exageradas em matemática, mas é importante reiterar o que realmente aconteceu.

Nós tinhamos um mensagem de 4, que queríamos manter em segredo. Nós aplicamos uma chave pública a ele, que nos deu a resultado criptografado de 688.749. Agora que está criptografado, podemos enviar com segurança o número 688.749 para o proprietário do par de chaves. Eles são a única pessoa capaz de descriptografá-lo com sua chave privada. Quando descriptografar, eles verão a mensagem que estávamos realmente enviando, 4.

Gerando a chave privada

Na criptografia RSA, depois que os dados ou uma mensagem são transformados em texto cifrado com uma chave pública, eles podem ser descriptografados apenas pela chave privada do mesmo par de chaves. As chaves privadas são compostas de d e n. Nós já sabemos n, e a seguinte equação é usada para encontrar d:

d = 1 /e mod λ(n)

No Gerando a chave pública seção acima, já decidimos que em nosso exemplo, e seria igual a 11. Da mesma forma, sabemos que λ(n) é igual a 349.716 de nosso trabalho anterior Função totiente de Carmichael. As coisas ficam um pouco mais complicadas quando encontramos esta seção da fórmula:

1 /e mod

Essa equação pode parecer que você está pedindo para dividir 1 por 11, mas esse não é o caso. Em vez disso, isso apenas simboliza que precisamos calcular o inverso modular do e (que neste caso é 11) e λ(n) (que neste caso é 349.716).

Isso significa essencialmente que em vez de executar uma operação de módulo padrão, usaremos o inverso. Isso normalmente é encontrado com o algoritmo euclidiano estendido, mas está um pouco fora do escopo deste artigo, portanto, trapacearemos e usaremos uma calculadora on-line. Agora que entendemos tudo o que está acontecendo, vamos inserir nossas informações na fórmula:

d = 1 /11 mod 349.716

Para executar esta operação, basta inserir 11 (ou qualquer valor que você possa ter para e se você estiver tentando isso com seu próprio exemplo), onde diz Inteiro e 349.716 (ou qualquer valor que você possa ter para λ(n) se você estiver tentando isso com seu próprio exemplo), onde diz Módulo na calculadora on-line que estava vinculada acima. Se você fez isso corretamente, deverá obter um resultado em que:

d = 254, 339

Agora que temos o valor para d, podemos descriptografar mensagens que foram criptografadas com nossa chave pública usando a seguinte fórmula:

m = cd mod n

Agora podemos voltar ao texto cifrado que criptografamos sob o Gerando a chave privada seção. Quando criptografamos a mensagem com a chave pública, isso nos deu um valor para c de 688.749. De cima, sabemos que d é igual a 254.339. Também sabemos que n é igual a 701.111. Isso nos dá:

m = 688.749254.339 mod 701.111.

Como você deve ter notado, tentar levar um número à 254.339ª potência pode ser um pouco demais para a maioria das calculadoras normais. Em vez disso, usaremos uma calculadora de descriptografia RSA online. Se você quisesse usar outro método, aplicaria os poderes como faria normalmente e executaria a operação do módulo da mesma maneira que fizemos no Gerando a chave pública seção.

Na calculadora vinculada acima, digite 701,111 onde diz Módulo de fornecimento: N, 254.399 onde diz Chave de descriptografia: D, e 688.749 onde diz Mensagem de texto cifrado em formato numérico, como mostrado abaixo:

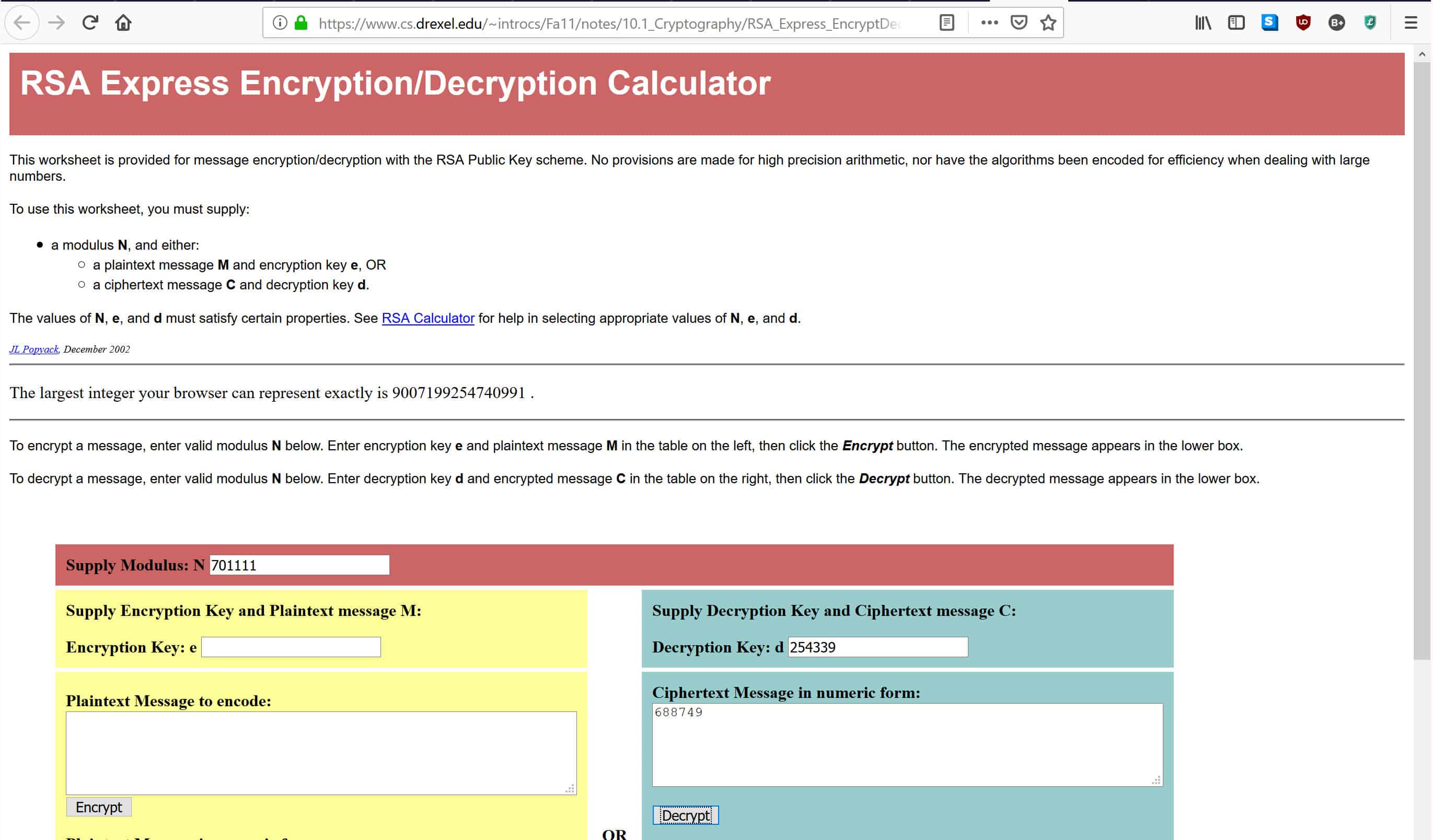
Depois de inserir os dados, pressione Descriptografar, que colocará os números na fórmula de descriptografia listada acima. Isso fornecerá a mensagem original na caixa abaixo. Se você fez tudo corretamente, deve obter uma resposta de 4, que foi a mensagem original que criptografamos com nossa chave pública.

Como a criptografia RSA funciona na prática

As seções acima devem fornecer uma compreensão razoável de como funciona a matemática por trás da criptografia de chave pública. Pode ser um pouco confuso, mas mesmo aqueles que não entenderam os meandros das equações podem tirar algumas informações importantes sobre o processo..

Nas etapas listadas acima, mostramos como duas entidades podem se comunicar com segurança sem ter compartilhado um código anteriormente. Primeiro, cada um deles precisa configurar seus próprios pares de chaves e compartilhar a chave pública uns com os outros. As duas entidades precisam manter suas chaves privadas em segredo para que suas comunicações permaneçam seguras.

Depois que o remetente tiver a chave pública de seu destinatário, ele poderá usá-la para criptografar os dados que deseja manter em segurança. Depois de criptografada com uma chave pública, ela só pode ser descriptografada pela chave privada do mesmo par de chaves. Mesmo a mesma chave pública não pode ser usada para descriptografar os dados. Isto é devido às propriedades de funções do alçapão que mencionamos acima.

Quando o destinatário recebe a mensagem criptografada, eles usam sua chave privada para acessar os dados. Se o destinatário quiser retornar as comunicações de maneira segura, eles podem criptografar sua mensagem com a chave pública da parte com a qual estão se comunicando. Novamente, depois de criptografada com a chave pública, a única maneira de acessar as informações é através da chave privada correspondente.

Dessa forma, a criptografia RSA pode ser usada por terceiros desconhecidos para enviar dados com segurança entre si. Partes significativas dos canais de comunicação que usamos em nossas vidas online foram criadas a partir dessa base.

Como as mensagens mais complicadas são criptografadas com o RSA?

No nosso exemplo, simplificamos muito as coisas para facilitar a compreensão, e é por isso que criptografamos apenas uma mensagem “4”. Ser capaz de criptografar o número 4 não parece particularmente útil, então você pode estar se perguntando como você pode criptografar um conjunto de dados mais complicado, como uma chave simétrica (que é o uso mais comum do RSA) ou até mesmo uma mensagem.

Algumas pessoas podem ficar perplexas com a maneira como uma chave como “n38cb29fkbjh138g7fqijnf3kaj84f8b9f…” ou uma mensagem como “compre um sanduíche para mim” pode ser criptografada por um algoritmo como o RSA, que lida com números e não letras. A realidade é que todas as informações que nossos computadores processam são armazenadas em binários (1s e 0s) e usamos padrões de codificação como ASCII ou Unicode representá-los de maneiras que os humanos possam entender (cartas).

Isso significa que teclas como “n38cb29fkbjh138g7fqijnf3kaj84f8b9f…” e mensagens como “compre um sanduíche para mim” já existem como números, que pode ser facilmente calculado no algoritmo RSA. Os números pelos quais eles são representados são muito maiores e mais difíceis de gerenciar, e é por isso que preferimos lidar com caracteres alfanuméricos em vez de uma mistura de números binários..

Se você quisesse criptografar uma chave de sessão mais longa ou uma mensagem mais complexa com o RSA, isso envolveria simplesmente um número muito maior.

Preenchimento

Quando o RSA é implementado, ele usa algo chamado preenchimento para ajudar a evitar uma série de ataques. Para explicar como isso funciona, começaremos com um exemplo. Digamos que você estava enviando uma mensagem codificada para um amigo:

Dear Karen,

    Eu espero que você esteja bem. Ainda estamos jantando amanhã?

    Com os melhores cumprimentos,

    James

Digamos que você codificou a mensagem de uma maneira simples, mudando cada letra para a que se segue no alfabeto. Isso mudaria a mensagem para:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

Se seus inimigos interceptaram esta carta, existe um truque que eles podem usar para tentar decifrar o código. Eles poderiam observe o formato da sua carta e tente adivinhar o que a mensagem pode estar dizendo. Eles sabem que as pessoas normalmente começam suas cartas com “Olá”, “Olá”, “Caro” ou várias outras convenções.

Se eles tentassem aplicar “Olá” ou “Olá” como a primeira palavra, veriam que não caberia no número de caracteres. Eles poderiam então tentar “Caro”. Cabe, mas isso não significa necessariamente nada. Os atacantes apenas tentavam e viam para onde os levavam. Assim, eles mudariam as letras “e”, “f”, “b” e “s” por “d”, “e”, “a” e “r”, respectivamente. Isso lhes daria:

Dear Laseo,

    J ipqe zpv são xemm. São xe tujmm iawjoh se diverte upnpsspx?

    Zpvrt tjoderemz,

    Kanet

Ainda parece bastante confuso, então os invasores podem tentar ver outras convenções, como a forma como concluímos nossas cartas. As pessoas costumam adicionar “De” ou “Atenciosamente” no final, mas nenhuma delas se encaixa no formato. Em vez disso, os atacantes podem tentar “Sinceramente” e substituir as outras letras para ver onde as leva. Alterando “z”, “p”, “v”, “t”, “j” “o”, “d” e “m” com “y”, “o”, “u”, “s”, “ i ”,“ n ”,“ c ”e“ l ”respectivamente, eles receberiam:

Dear Lasen,

    Eu ioqe você é xell. São xe tuill iawinh dinnes uonossox?

    Com os melhores cumprimentos,

    Kanet

Após essa modificação, parece que os atacantes estão começando a chegar a algum lugar. Eles encontraram as palavras “eu”, “você” e “são”, além das palavras que compunham suas suposições iniciais.

Como as palavras estão na ordem gramatical correta, os atacantes podem ter certeza de que estão seguindo na direção certa. Até agora, eles provavelmente também perceberam que o código envolvia cada letra sendo alterada para a que se segue no alfabeto. Uma vez que eles percebem isso, fica fácil traduzir o restante e ler a mensagem original.

O exemplo acima era apenas um código simples, mas como você pode ver, a estrutura de uma mensagem pode fornecer aos invasores pistas sobre seu conteúdo. Certamente, foi difícil descobrir a mensagem apenas a partir de sua estrutura e foram necessárias algumas suposições, mas você deve ter em mente que os computadores são muito melhores nisso do que nós.. Isso significa que eles podem ser usados ​​para descobrir códigos muito mais complexos em um tempo muito menor, com base em pistas que vêm da estrutura e outros elementos.

Se a estrutura pode causar a quebra de um código e revelar o conteúdo de uma mensagem, precisamos de uma maneira de ocultar a estrutura para manter a mensagem segura. Isso nos leva a preenchimento.

Quando uma mensagem é preenchida, Dados aleatórios são adicionados para ocultar as dicas de formatação originais que podem levar à quebra de uma mensagem criptografada. Com o RSA, as coisas ficam um pouco mais complicadas, porque uma chave criptografada não possui a formatação óbvia de uma carta que nos ajudou a fornecer pistas no exemplo acima..

Apesar disso, os adversários podem usar vários ataques para explorar as propriedades matemáticas de um código e quebrar dados criptografados. Devido a esta ameaça, implementações do RSA usam esquemas de preenchimento como OAEP para incorporar dados extras na mensagem. A adição desse preenchimento antes da criptografia da mensagem torna o RSA muito mais seguro.

Assinando mensagens

O RSA pode ser usado para mais do que apenas criptografar dados. Suas propriedades também o tornam um sistema útil para confirmando que uma mensagem foi enviada pela entidade que alega enviá-la, além de provar que uma mensagem não foi alterada ou adulterada.

Quando alguém quer provar a autenticidade de sua mensagem, pode calcular uma cerquilha (uma função que pega dados de tamanho arbitrário e os transforma em um valor de tamanho fixo) do texto sem formatação e, em seguida, assine-o com sua chave privada. Eles assine o hash aplicando a mesma fórmula usada na descriptografia (m = cd mod n) Depois que a mensagem é assinada, eles enviam essa assinatura digital ao destinatário junto com a mensagem.

Se um destinatário receber uma mensagem com uma assinatura digital, ele poderá usar o assinatura para verificar se a mensagem foi autenticamente assinada pela chave privada da pessoa que alega ter enviado. Eles também podem ver se a mensagem foi alterada pelos atacantes após o envio.

Para verificar a assinatura digital, o destinatário primeiro usa a mesma função de hash para encontrar o valor de hash da mensagem que recebeu. O destinatário então aplica o chave pública do remetente para a assinatura digital, usando a fórmula de criptografia (c = me mod n), para dar a eles o hash da assinatura digital.

Por comparando o hash da mensagem que foi recebida juntamente com o hash da assinatura digital criptografada, o destinatário pode dizer se a mensagem é autêntica. Se os dois valores forem iguais, a mensagem não foi alterada desde que foi assinada pelo remetente original. Se a mensagem tivesse sido alterada por um único caractere, o valor do hash seria completamente diferente.

Segurança RSA & ataques

Como a maioria dos sistemas de criptografia, a segurança do RSA depende de como ele é implementado e usado. Um fator importante é o tamanho da chave. o quanto maior o número de bits em uma chave (essencialmente quanto tempo ela é), mais difícil é atravessar os ataques como força bruta e fatoração.

Como algoritmos de chave assimétrica, como o RSA, podem ser quebrados pela fatoração de número inteiro, enquanto algoritmos de chave simétrica, como o AES, não podem, as chaves do RSA precisam ser muito mais longas para atingir o mesmo nível de segurança..

Atualmente, o O maior tamanho de chave que foi fatorado tem 768 bits. Isso foi feito por uma equipe de acadêmicos durante um período de dois anos, usando centenas de máquinas.

Desde que o fatoramento foi concluído no final de 2009 e o poder da computação cresceu significativamente desde então, pode-se supor que uma tentativa de intensidade semelhante agora pode fatorar uma chave RSA muito maior.

Apesar disso, o tempo e os recursos necessários para esse tipo de ataque o colocam fora do alcance da maioria dos hackers e no âmbito dos estados-nação. O melhor tamanho de chave a ser usado dependerá do seu modelo de ameaça individual. O Instituto Nacional de Padrões e Tecnologia recomenda um tamanho mínimo de chave de 2048 bits, mas chaves de 4096 bits também são usadas em algumas situações em que o nível de ameaça é maior.

O fatoramento é apenas uma das maneiras pelas quais o RSA pode ser quebrado. Vários outros ataques têm o potencial de interromper a criptografia com uma quantidade menor de recursos, mas isso depende da implementação e de outros fatores, não necessariamente do próprio RSA. Alguns destes incluem:

Os primos são realmente aleatórios?

Algumas implementações do RSA usam geradores de números aleatórios fracos para criar os primos. Se esses números não forem suficientemente aleatórios, será muito mais fácil para os invasores os fatorarem e quebrarem a criptografia. Este problema pode ser evitado usando um gerador de números pseudo-aleatórios criptograficamente seguro.

Má geração de chaves

As chaves RSA precisam estar dentro de certos parâmetros para garantir sua segurança. Se os primos p e q estão muito próximos, a chave pode ser facilmente descoberta. Da mesma forma, o número d que faz parte da chave privada não pode ser muito pequena. Um valor baixo facilita a solução. É importante que esses números tenham comprimento adequado para manter sua chave em segurança.

Ataques de canal lateral

Esse é um tipo de ataque que não interrompe o RSA diretamente, mas usa as informações de sua implementação para fornecer aos invasores dicas sobre o processo de criptografia. Esses ataques podem incluir coisas como analisando a quantidade de energia que está sendo usada, ou análise de previsão de ramificação, que usa medições de tempo de execução para descobrir a chave privada.

Outro tipo de ataque de canal lateral é conhecido como ataque de tempo. Se um invasor puder medir o tempo de descriptografia no computador de seu alvo para várias mensagens criptografadas diferentes, essas informações podem possibilitar ao invasor verificar a chave privada do alvo.

A maioria das implementações do RSA evita esse ataque adicionando um valor único durante o processo de criptografia, o que remove essa correlação. Esse processo é chamado cegamento criptográfico.

A criptografia RSA é segura para o futuro?

A boa notícia é que o RSA é considerado seguro, apesar desses possíveis ataques. A ressalva é que ele precisa ser implementado corretamente e usar uma chave dentro dos parâmetros corretos. Como acabamos de discutir, as implementações que não usam preenchimento, usam números primos de tamanho inadequado ou têm outras vulnerabilidades não podem ser consideradas seguras.

Se você deseja usar a criptografia RSA, verifique se você está usando uma chave de pelo menos 1024 bits. Aqueles com modelos de ameaças mais altas devem usar chaves de 2048 ou 4096 bits, se quiserem usar o RSA com confiança. Desde que você esteja ciente dos pontos fracos que o RSA possui e use-o corretamente, você deve se sentir seguro para usá-lo para compartilhamento de chaves e outras tarefas semelhantes que exijam criptografia de chave pública.

Veja também: Tipos de criptografia comuns explicados