O que é criptografia 3DES e como o DES funciona?

3DES é uma cifra de criptografia que foi derivada do Data Encryption Standard (DES) original. Tornou-se proeminente no final dos anos 90, mas desde então caiu em desuso devido ao aumento de algoritmos mais seguros.

Embora seja descontinuado em 2023, ainda é implementado em algumas situações. Como é baseado em um dos primeiros algoritmos amplamente publicados e estudados, o DES, ainda é importante aprender sobre o que é o 3DES e como ele funciona..

Este guia o guiará por cada etapa do processo do DES em detalhes e, em seguida, abordará como o DES é modificado no 3DES para torná-lo mais seguro. Ele também aborda os vários problemas de segurança e se você deve ou não usar o algoritmo.

O que é o 3DES?

Embora seja oficialmente conhecido como Algoritmo de criptografia de dados triplo (3DEA), é mais conhecido como 3DES. Isso ocorre porque o algoritmo 3DES usa a cifra padrão de criptografia de dados (DES) três vezes para criptografar seus dados.

DES é um algoritmo de chave simétrica baseado em uma rede Feistel. Como uma cifra de chave simétrica, ela usa a mesma chave para os processos de criptografia e descriptografia. A rede Feistel torna esses dois processos quase exatamente iguais, o que resulta em um algoritmo mais eficiente de implementar.

O DES possui um tamanho de bloco e chave de 64 bits, mas, na prática, a chave concede apenas 56 bits de segurança. O 3DES foi desenvolvido como uma alternativa mais segura devido ao pequeno tamanho da chave do DES. No 3DES, o algoritmo DES é executado três vezes com três chaves, no entanto, só é considerado seguro se três chaves separadas forem usadas.

Os usos do 3DES

Uma vez que as fraquezas do DES normal se tornaram mais aparentes, o 3DES foi adotado em uma ampla gama de aplicações. Foi um dos esquemas de criptografia mais usados ​​antes do surgimento do AES.

Alguns exemplos de suas implementações incluem sistemas de pagamento Microsoft Office, Firefox e EMV. Muitas dessas plataformas não usam mais o 3DES porque existem alternativas melhores.

O Instituto Nacional de Padrões e Tecnologia (NIST) lançou um projeto de proposta dizendo que todas as formas de 3DES serão obsoletas até 2023 e proibidas a partir de 2024 em diante. Embora seja apenas um rascunho, a proposta significa o fim de uma era e já passou da hora de passar para outros algoritmos mais seguros.

A história da criptografia 3DES

Como o 3DES é derivado do DES, é melhor introduzir primeiro o padrão anterior. Nos anos setenta, o National Bureau of Standards (NBS – desde então renomeado para NIST) procurava um algoritmo que pudesse ser usado como padrão para criptografar informações governamentais confidenciais, ainda não classificadas..

A NBS aceitou propostas para um padrão que atendesse aos seus requisitos, mas nenhum dos candidatos da rodada original era apropriado. Ele convidou mais submissões, e desta vez a IBM enviou através de um algoritmo que sua equipe desenvolveu. A submissão foi derivada da cifra de Lúcifer que Horst Feistel projetou.

Em 1975, o algoritmo IBM foi publicado pela NBS como o padrão de criptografia de dados proposto. O público foi convidado a comentar o projeto, o que atraiu algumas críticas.

Criptografadores de destaque como Whitfield Diffie e Martin Hellman, designers da troca de chaves Diffie-Hellman, alegaram que o comprimento da chave era muito curto e que as caixas S haviam sido alteradas em relação ao design inicial.

Na época, muitos membros da comunidade criptográfica pensavam que a NSA havia sabotado o projeto e enfraquecido o algoritmo, de modo que seria a única agência que poderia quebrar o DES.

Quando isso foi investigado pelo Comitê de Inteligência do Senado dos Estados Unidos, verificou-se que a “NSA convenceu a IBM de que um tamanho reduzido de chave era suficiente; indiretamente auxiliado no desenvolvimento das estruturas S-box; e certificou que o algoritmo final do DES estava, dentro do seu conhecimento, livre de qualquer fraqueza estatística ou matemática “.

O mesmo relatório dizia que “a NSA não alterou o design de forma alguma”. Isso foi apoiado por alguns ex-funcionários da IBM que alegaram que o algoritmo DES foi projetado inteiramente pela equipe da IBM.

A documentação desclassificada da NSA afirma que a agência “trabalhou em estreita colaboração com a IBM para fortalecer o algoritmo contra todos, exceto ataques de força bruta, e para fortalecer tabelas de substituição …”

As suspeitas de adulteração da NSA foram atenuadas nos anos noventa, uma vez que a criptoanálise diferencial foi descoberta publicamente. Quando as S-boxes, muito difamadas, foram testadas com a nova técnica, mostraram-se mais resistentes ao ataque do que se tivessem sido escolhidas aleatoriamente.

Isso indica que a equipe da IBM já sabia sobre a análise criptográfica diferencial nos anos setenta, com Steven Levy alegando que a NSA pediu que eles mantivessem a técnica em segredo para proteger a segurança nacional.

O famoso criptógrafo Bruce Schneier disse uma vez: “Levou duas décadas para a comunidade acadêmica descobrir que os ‘ajustes’ da NSA na verdade melhoravam a segurança do DES”.

Apesar das perguntas iniciais sobre a segurança do algoritmo e o envolvimento da NSA, o algoritmo da IBM foi aprovado como o padrão de criptografia de dados em 1976. Foi publicado em 1977 e reafirmado como padrão em 1983, 1988 e 1993.

Quando a criptoanálise linear foi publicada pela primeira vez em 1994, ela começou a levantar questões sobre a segurança do algoritmo. Em 1997, o NIST anunciou que estava procurando um algoritmo para substituir o DES. A necessidade de um novo algoritmo foi intensificada à medida que a tecnologia se desenvolveu e os ataques em potencial ficaram mais fortes.

Várias tentativas de quebra mostraram que era menos difícil quebrar o algoritmo do que se pensava anteriormente. Em 1998, a Distribut.net conseguiu quebrar o DES há 39 dias.

No início de 1999, o Deep Crack da Electronic Frontier Foundation reduziu o tempo para pouco mais de 22 horas. Isso sinalizou o fim do DES, já que um ataque dessa natureza estava agora ao alcance de um adversário com bons recursos.

A questão principal era o pequeno espaço-chave, e um novo algoritmo era extremamente necessário. Isso foi um problema, porque levaria vários anos para o NIST se instalar no algoritmo que se tornou o padrão de substituição, o Advanced Encryption Standard (AES).

Enquanto a cifra da AES estava sendo decidida, o 3DES foi proposto como uma medida paliativa. Envolve a execução do algoritmo DES três vezes, com três chaves separadas. Em 1999, o DES foi reafirmado, mas com o 3DES como o algoritmo ideal. O DES normal foi permitido apenas em aplicativos herdados.

O 3DES tornou-se um algoritmo de criptografia generalizado, embora seu uso intenso de recursos e limitações de segurança tenham levado a ser substituído pelo AES na maioria dos casos de uso.

Entendendo o algoritmo DES

Antes de podermos falar sobre os detalhes do 3DES, é importante entender o algoritmo DES do qual ele derivou. Então, vamos começar logo no começo.

Usamos a criptografia para transformar nossos dados de texto sem formatação em texto cifrado, que são informações que não podem ser acessadas por atacantes (desde que utilizemos algoritmos apropriados).

Os algoritmos de criptografia são essencialmente fórmulas matemáticas complexas. Quando se trata de criptografar algo como “Vamos à praia”, muitas pessoas ficam confusas. Afinal, como você pode aplicar matemática a coisas como letras e caracteres?

Codificando o texto

A realidade é que os computadores não lidam com letras e caracteres. Em vez disso, eles trabalham em um sistema de 1s e 0s conhecido como binário. Cada 1 ou 0 é conhecido como um bit e uma coleção de oito deles é conhecida como um byte.

Você pode procurar manualmente ou usar um conversor on-line para ver que, em binário, “Vamos à praia” se torna:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

Blocos

Quando os dados são criptografados, eles são divididos em blocos separados para processamento. O DES possui um tamanho de bloco de 64 bits, o que significa essencialmente que cada bloco se encaixa em uma mistura de 64 unidades e zeros. Nosso primeiro bloco (os primeiros 64 dígitos do binário mostrado acima) seria:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Nosso segundo seria:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

E nosso bloco final seria:

01100010 01100101 01100001 01100011 01101000

Preenchimento

Você deve ter notado que nosso terceiro bloco tem apenas 40 bits. Antes de poder ser criptografado, ele precisa ter um tamanho de bloco de 64 bits. Isso é feito com preenchimento, o que envolve adicionar informações extras a um bloco para concluí-lo. Isso pode ser feito com vários esquemas diferentes e também pode ajudar a dificultar a quebra de informações criptografadas, mas não abordaremos isso neste artigo.

A programação chave do DES

Os algoritmos de criptografia usam chaves para adicionar dados que alterarão o resultado final do processo. Se o DES envolver apenas etapas como permutação e caixas S (a permutação é explicada abaixo, enquanto as caixas S são cobertas no Substituição seção), tudo o que um invasor precisa fazer é descobrir os detalhes do algoritmo e executar cada uma das etapas ao contrário para revelar a mensagem inicial.

Como a maioria dos nossos algoritmos é amplamente conhecida, isso não adicionaria muita segurança. Em vez disso, chaves secretas são adicionadas para alterar a saída de uma maneira que não pode ser prevista apenas conhecendo o algoritmo (desde que um algoritmo suficientemente complexo seja usado).

O DES começa com uma única chave, usada para criar subchaves aplicadas em cada rodada. Essa é uma chave de 64 bits, que tem o mesmo tamanho dos nossos blocos. Digamos que nossa chave é:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Agora, essa chave é digitada em binário, que é a maneira como os dados são expressos quando os computadores os processam. Quando os humanos lidam com as chaves, elas normalmente aparecem como uma mistura de caracteres, algo como isto:

kj329nf982bc9wn1

No DES, o primeiro passo para derivar nossas teclas redondas é permutar a chave (movê-la) de acordo com a tabela a seguir:

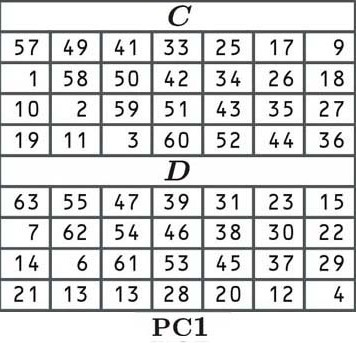
Na permutação, cada bit da nossa chave original é embaralhado para uma nova posição, conforme indicado na tabela. Como a célula no canto superior esquerdo (de C) diz 57, o primeiro número da nossa chave permutada será o número na 57a posição do nosso antigo bloco:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

A segunda célula diz 49., o que significa que o segundo dígito da nossa nova chave será o número que está na 49a posição do nosso bloco antigo:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

A terceira célula diz 41., então procuramos o dígito na 41ª posição:

01001010 10101101 11101000 10100101 01110001 0 01010100 10101001 1111010

Até agora, nossa chave é composta de “110“.

O restante da chave é organizado da mesma maneira, de acordo com os valores da tabela. Movemo-nos da esquerda para a direita e, quando chegamos ao final de uma linha, pulamos para a próxima, como normalmente. Uma vez tabela C está terminado, pulamos para tabela D para completar a segunda metade da chave.

Não há uma maneira fácil de transpor todo o nosso bloco de acordo com a tabela de permutação inicial. Você pode fazer tudo manualmente, ou escrever um script para ele (ou até ter sorte e encontrar um nas profundezas da Internet), mas vamos trapacear e inventar:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

Você pode estar preocupado com o fato de estarmos inventando alguns dos números deste guia, mas a realidade é que isso realmente não importa. Ninguém mais criptografa dados manualmente, tudo é feito por meio de programas. O aspecto mais crítico deste tutorial é que você obtém uma idéia clara dos conceitos com os quais estamos lidando. Os próprios números servem apenas para ajudá-lo a visualizar o que está acontecendo.

Alguns leitores podem ter notado que a tabela (e agora nossa chave) possui apenas 56 bits em vez de 64. Isso ocorre porque todo oitavo bit é ignorado. Este é um artefato dos dias mais antigos da tecnologia, quando era importante ter bits de verificação de paridade, que verificavam se a chave havia sido recebida corretamente. Esses bits de verificação de paridade significam que, na prática, o DES tem apenas a segurança de uma chave de 56 bits.

As tabelas C e D nos fornecem uma chave que possui duas metades de 28 bits. Às vezes, as metades são referidas como C e D, mas, ao longo deste artigo, vamos nos referir a elas como L e R, para esquerda e direita. Nosso lado esquerdo é:

1100010 1010010 1010101 0101010

Enquanto nosso direito é:

1010000 1111001 0001011 1000111

O próximo passo é deslocar a tecla em um ou dois espaços para a esquerda, dependendo da rodada. O número exato de espaços é decidido de acordo com a seguinte tabela predeterminada:

Número de turnos para a esquerda

1	1
2	1
3	2
4	2
5	2
6	2
7	2
8	2
9	1
10	2
11	2
12	2
13	2
14	2
15	2
16	1

Então, vamos dar as metades esquerda e direita:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

E desloque os dois uma posição para a esquerda, pois o primeiro turno tem um deslocamento de 1 de acordo com a tabela (o número na extremidade esquerda é movido para a extremidade direita).

Subchave da primeira rodada:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

Na segunda rodada, a tabela também diz 1, então esse resultado será alterado novamente movendo cada posição número um para a esquerda.

Segunda rodada sub-chave:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

Na terceira rodada, os números serão movidos dois lugares para a esquerda, porque a tabela agora diz 2.

Subchave da terceira rodada:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

Nas rodadas subsequentes, os números são movidos para a esquerda de acordo com as distâncias especificadas na tabela, com cada turno sendo aplicado ao resultado da rodada anterior. No final, isso nos dá dezesseis subchaves diferentes, uma para cada rodada do processo DES.

O próximo passo é outra permutação de acordo com a tabela PC2 mostrada abaixo:

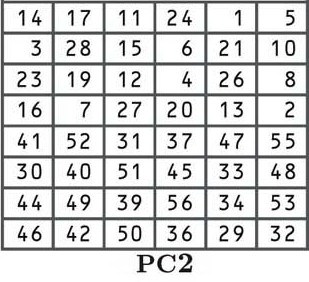
Até agora, você deve estar familiarizado com as permutações, para que não entremos no processo em profundidade. Se você quiser ver como ele funciona com mais detalhes, consulte a explicação no início desta seção. Embora as posições de realocação sejam diferentes, o processo é o mesmo.

Cada uma das 16 teclas derivadas no processo de mudança agora é embaralhada de acordo com a tabela, com o número da 14ª posição movido para o primeiro lugar, a 17ª para a segunda, a 11ª para a terceira, etc…

Se você olhar atentamente para a tabela, notará que existem apenas 48 bits, em vez dos 56 bits que tínhamos anteriormente. Esse processo é conhecido como permutação por compressão.

Você também pode ver que a metade superior da tabela apresenta números entre um e 28, enquanto a metade inferior contém números de 29 a 56. Isso mantém as metades esquerda e direita de nossas subchaves separadas e é indicado abaixo pelo espaço maior no meio das teclas.

Mais uma vez, vamos trapacear e inventar os números. Digamos que todo esse processo nos deu as seguintes subchaves:

Primeiro round:         010101 010101 101010 110100 101001 100101 101010 101010

Segundo round:         011010 110101 101110 110010 010100 110010 111101 101101

Rodada três:     010100 100110 110110 101010 100110 011000 101011 011001

Rodada quatro:         011001 110101 011001 110101 000011 001011 010101 010101

Rodada cinco:         110101 001101 010101 010101 010011 001011 010111 100101

Rodada seis:           010111 110101 011001 111001 101001 100101 101010 101010

Rodada sete:     110101 111010 101110 101010 100110 010110 111011 001110

Rodada oito:       011001 110101 010101 001001 010011 001011 010100 101010

Rodada nove:         111011 011010 011110 100010 100010 010110 110011 110010

Rodada 10:             011010 010101 101110 101001 010010 010110 111000 101010

Rodada 11:             110101 001101 101110 101010 100101 100101 101010 001010

Rodada 12:             101001 100100 101001 101010 100110 011000 101011 011001

Rodada 13:             010010 010010 010101 010101 010110 110001 100101 101010

Rodada 14:             101001 100110 010101 011101 010001 001010 110010 111110

Rodada 15:             011001 011010 011001 110101 001001 011001 100101 101101

Rodada 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Esse processo de mudança resulta em cada bit da chave inicial sendo usado em cerca de 14 das 16 subchaves, embora alguns bits sejam usados ​​um pouco mais do que outros.

Permutação inicial

Depois que os dados forem divididos em blocos e preenchidos, se necessário, é hora de começar o processo de criptografia DES. Voltaremos às subchaves que acabamos de criar posteriormente. A primeira etapa é conhecida como permutação inicial, onde os dados são reorganizados de acordo com a tabela a seguir:

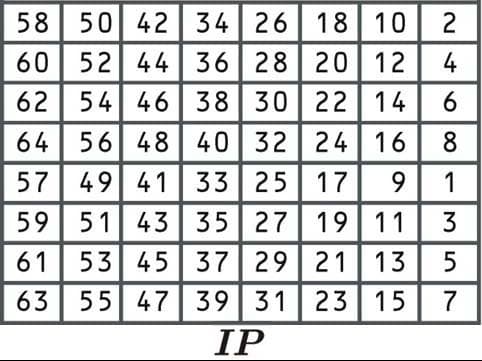
Esse processo inicial de permutação não torna o algoritmo mais seguro. Isso ocorre porque não envolve a entrada de nenhuma chave e pode ser facilmente revertida. O algoritmo foi originalmente projetado dessa maneira, porque facilitou a implementação em certos contextos.

Como cobrimos permutações algumas vezes, ignoraremos qualquer explicação importante aqui. Volte para A programação chave do DES seção, se você precisar de mais informações sobre como eles funcionam.

Vamos dar o primeiro quarteirão da mensagem “Vamos para a praia”, que derivamos no Quadra seção sob Entendendo o algoritmo DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Desde a primeira célula diz 58., selecionaríamos o número da 58ª posição:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Em seguida, pegaríamos o número da 50ª posição:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

E o número da 42ª posição:

01001100 01100101 01110100 00100111 01110011 00 0100000 01100111 01101111

Isso nos dá “110” tão longe. Vamos compor o resto do número:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Quando a permutação inicial é concluída, os dados são movidos para a próxima etapa.

Dividindo os blocos

Depois que os dados passam por sua permutação inicial, são divididos em duas metades. Tomamos nosso bloco que passou por sua permutação inicial:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

E vamos separá-lo em dois blocos, um bloco esquerdo (composto dos primeiros 32 dígitos), conhecido como eu0 0:

eu0 0    11010111 01001010 10101000 10011101

E um bloco direito (composto pelos segundos 32 dígitos), conhecido como R0 0:

R0 0    01001011 10110101 10000111 10101001

A função F

Agora que o bloco foi dividido, é hora da função F ocorrer. Na primeira rodada, ele será aplicado apenas na metade direita do bloco, enquanto a metade esquerda é mantida de lado até mais tarde. O lado direito realiza as quatro etapas a seguir como parte da função F:

• Permutação de expansão (E no diagrama)
• Mistura de teclas (⊕ no diagrama)
• Substituição (cada S1, S2 etc. no diagrama)
• Permutação (P no diagrama)

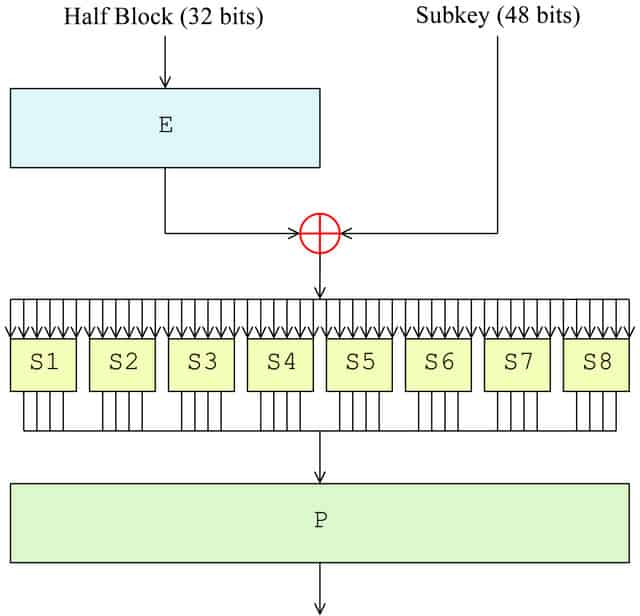
Permutação de expansão

A permutação de expansão realiza três coisas. O mais importante é que ele permite que bits únicos de dados de entrada afetem a saída de outros dois bits, causando um efeito de avalanche. Ele também cria a metade direita de 48 bits, de modo que tenha o mesmo tamanho da subchave para a próxima etapa. O outro efeito da permutação de expansão é que ela prolonga a saída que a entrada. Isso permite que ele seja compactado na operação de substituição.

Os bits são reorganizados de acordo com a tabela a seguir. Alguns dos bits individuais estão na tabela duas vezes, e é assim que o bloco se expandiu de 32 para 48 bits:

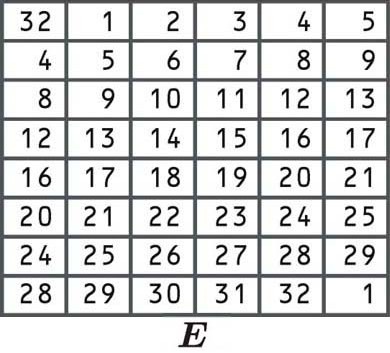
Como a primeira célula diz 32, pegamos nosso bloco direito e selecionamos o número da 32ª posição, assim como fizemos nos outros exemplos de permutação listados acima:

R0 0    01001011 10110101 10000111 10101001

Em seguida, pegamos os números da primeira posição, da segunda posição e assim por diante, até chegarmos ao canto inferior direito do bloco. Como existe uma 1 nesta célula, o último dígito também será o número que aparece na primeira posição do nosso bloco.

Digamos que a permutação de expansão nos dê um novo bloco de 48 bits:

101110 100110 100100 000000 001100 001110 101101 011110

Mistura de teclas

Depois que o bloco for expandido para 48 bits, é hora de aplicar a subchave da primeira rodada, que derivamos na Programação chave do DES seção acima. O bloco é modificado pela subchave usando a cifra XOR.

A cifra XOR é uma cifra adicional que segue um processo simples, especialmente quando comparado a outros elementos que já discutimos.

Em uma cifra XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Então, digamos que você precise XOR os dois números a seguir em binário:

1101

0101

Cada dígito seria adicionado ao abaixo. De acordo com as três regras mostradas acima, isso resulta em:

1000

Para concluir a etapa de mixagem de teclas, tomamos o lado direito do nosso bloco que acabamos de expandir para 48 bits e a primeira tecla redonda. Em seguida, executamos a adição do XOR:

Quadra:                      101110 100110 100100 000000 001100 001110 101101 011110

Chave redonda:     010101 010101 101010 110100 101001 100101 101010 101010

Resultado XOR:             111011 110011 001110 110100 100101 101011 000111 110100

O resultado da operação XOR é passado para a próxima rodada.

Substituição

Substituição adiciona confusão aos dados. Normalmente, isso é feito com tabelas de pesquisa, também conhecidas como caixas de substituição ou S-boxes. O DES usa oito tabelas ou S-boxes separadas, uma diferente para cada 6 bits de dados. A tabela a seguir mostra as oito caixas S do DES:

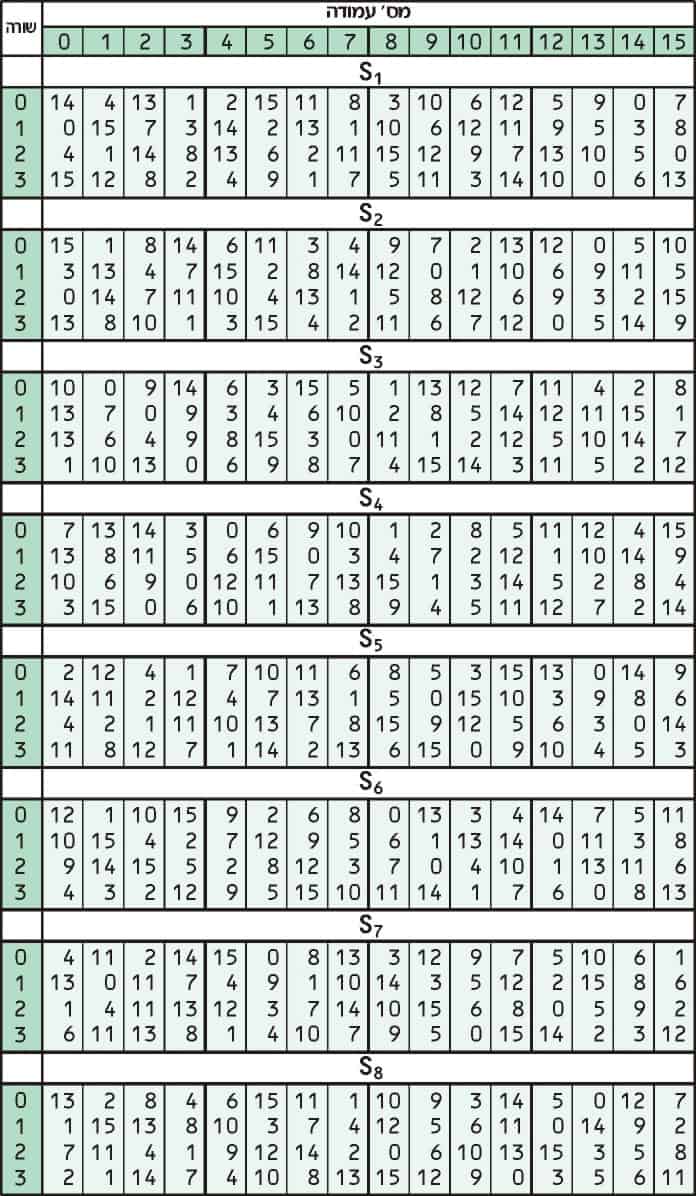
As oito caixas S separadas são usadas para converter cada entrada de 6 bits em uma saída de 4 bits. A primeira etapa do processo é pegar os dígitos no início e no final de um segmento de 6 bits e converter esse valor binário em decimal.

Vamos pegar os dados que acabamos de concluir o XOR na etapa anterior:

111011 110011 001110 110100 100101 101011 000111 110100

Veremos o primeiro segmento de 6 bits para mostrar como o processo de substituição funciona:

111011

Como o primeiro e o último número são ambos 1, isso nos dá um valor de 11. Depois convertemos 11 de binário para decimal, o que nos dá 3. Estes são apenas valores equivalentes, escritos de maneiras diferentes. Pense nisso como converter a linguagem de computador em linguagem humana. Você pode conferir a conversão você mesmo com uma calculadora on-line, se quiser.

Em seguida, pegamos os quatro dígitos do meio do primeiro segmento de 6 bits:

111011

E converta-os de binário para decimal. 1101 traduz para o número 13.

Agora, pegamos esses dois números e os procuramos no S1 mesa:

               

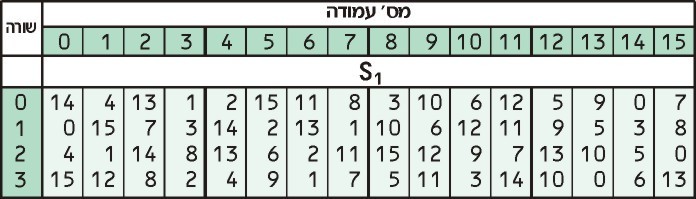
Nosso primeiro número, 3, nos diz para olhar na terceira linha, enquanto nosso segundo número, 13 nos diz para procurar na 13ª coluna. O valor na terceira linha da 13ª coluna é 0 0.

Agora que procuramos nosso número na tabela, o convertemos novamente em binário de quatro dígitos. Zero normalmente é escrito como 0 em binário, mas 0000 é o mesmo e esse é o formato mais adequado para nossos propósitos.

Após esse processo, a caixa S converte nossa primeira seção de dados de 6 bits (111011) em um valor diferente de 4 bits (0000) Parece complicado, mas essa técnica ajuda a obscurecer ainda mais a relação entre o texto cifrado e o texto simples ao qual está vinculado.

A próxima seção de dados de 6 bits passa pelo mesmo processo, mas usa a caixa S2 mostrada acima. A terceira seção usa a tabela S3 e assim por diante, até a seção final ser substituída pela tabela S8.

Mais uma vez, vamos trapacear com o restante dos valores. Digamos que as caixas de substituição nos dê um resultado de:

0000 1010 1100 1001 0100 1001 0111 0001

Depois que cada seção dos dados passa pela caixa S, ela passa para a próxima etapa.

Permutação

O último estágio da função F é outra permutação, usando a seguinte tabela: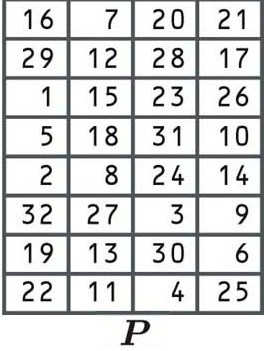

Até agora, você deve ter um entendimento decente de como as permutações mudam os dígitos do bloco antigo para uma posição diferente no novo bloco, para que não voltemos a usá-lo novamente..

Digamos que essa permutação tenha nosso resultado anterior:

0000 1010 1100 1001 0100 1001 0111 0001

E nos fornece uma saída de:

0101 0110 1001 0101 0010 0100 0101 0010

Agora que a permutação foi concluída, concluímos as quatro etapas da função F nesta rodada. Em notação matemática, esse valor é conhecido como f (R0 0, K1). Isso significa que o resultado é a função (f) do lado direito inicial do bloco (R0) e da subchave da primeira rodada (K1).

XOR com o bloco esquerdo

Lembra-se de como dividimos o bloco ao meio antes de começarmos as etapas da função F? Separamos o lado esquerdo do bloco (L0), enquanto o lado direito passou por cada um desses processos. Bem, agora é hora de L0 voltar à ação.

Tomamos o lado certo que acabamos de processar f (R0 0, K1) e adicione-o ao lado esquerdo antigo (eu0 0) usando a cifra XOR. Isso nos dá R1, o resultado da nossa primeira rodada:

f (R0 0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

eu0 0:                                    1101 0111 0100 1010 1010 1000 1001 1101

Resultado XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Consulte o Mistura de teclas seção acima, se você precisar de um lembrete de como a cifra XOR funciona.

Mais 15 rodadas…

Se você chegou até aqui, o DES provavelmente parece um processo árduo. Mas ainda não está nem perto de terminar. Os dados seguem as quatro etapas da função F, seguidas pelo XOR, outras 15 vezes, para um total de 16 rodadas.

Na segunda rodada, pegamos a versão original e intocada do lado direito do bloco (R0) e o tornamos o novo lado esquerdo (L1). Enquanto isso, pegamos o resultado da primeira rodada e o enviamos pela função F. Tudo acontece da mesma forma que da última vez, mas desta vez a subchave da segunda rodada é usada. Digamos que esse processo nos dê um resultado de:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Em seguida, XOR o resultado com L1, que na verdade é R0 (derivamos isso no Blocos de divisão seção). Isso nos dá o resultado do segundo turno, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

eu1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Essa etapa pode parecer um pouco confusa, mas, sob o esquema Feistel, o antigo lado direito se torna a nova esquerda, enquanto o resultado da operação se torna o novo lado direito.

O diagrama a seguir fornece uma representação visual do que está acontecendo. IP representa a permutação inicial, F é um substituto para toda a função F, ⊕ simboliza a função XOR e as setas indicam cada lado do bloco se movendo entre esquerda e direita:

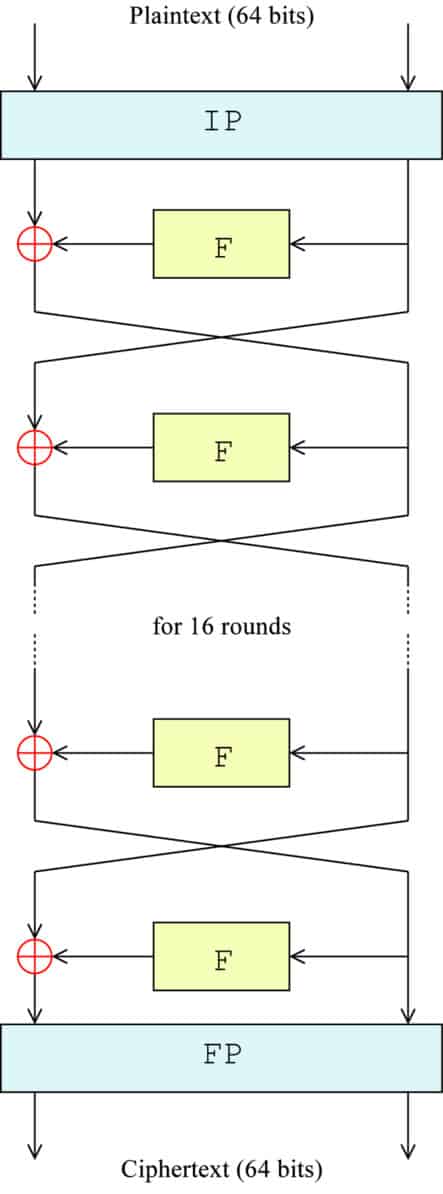
A fórmula exata para cada etapa é:

eun = Rn-1

Rn = eun-1 + f(Rn-1,Kn)

Onde:

L = A metade esquerda do bloco (começando com L0 quando o bloco foi inicialmente dividido)

R = A metade direita do bloco (começando com R0 quando o bloco foi inicialmente dividido)

n = O número da rodada (começando com 0, quando o bloco foi inicialmente dividido)

f = A função F

Kn = A subchave da rodada n

De acordo com a fórmula e o diagrama, no terceiro turno, R1 se torna a nova metade esquerda (L2), enquanto R2 é processado através da função F. Digamos que isso nos dê um resultado de:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Em seguida, calculamos o resultado da terceira rodada (R3), usando a cifra XOR, assim como antes:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

eu2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

O mesmo processo continua até a décima quinta rodada, com a alternância dos blocos e a próxima subchave sendo usada em cada rodada. Na 16ª e última rodada, os blocos não são trocados. Em vez disso, eles são combinados para formar um bloco de 64 bits. Evitar trocar os blocos neste último estágio permite que o algoritmo seja usado para criptografia e descriptografia.

Digamos que a rodada final nos dê um resultado de:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Permutação final

Essa permutação é o inverso da permutação inicial e, novamente, não agrega nenhum valor extra de segurança. Reorganiza os dados de acordo com a seguinte tabela:

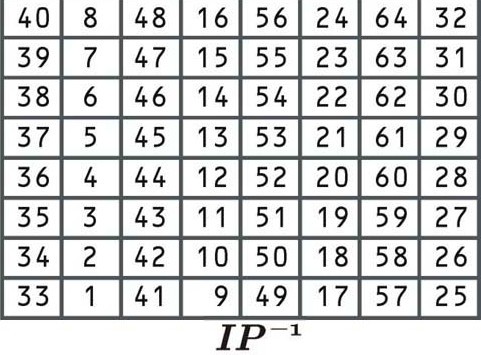
Esta tabela de permutação funciona da mesma forma que as anteriores. Como é a etapa final do processo de criptografia, o resultado será o texto cifrado para o primeiro bloco de “Vamos para a praia”. Digamos que o bloco criptografado seja:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Agora, se você quisesse o texto cifrado real para “Vamos à praia”, poderia ter pulado todo o processo de aprendizado e ido direto para uma ferramenta de criptografia DES online. Se inserirmos a sentença ao lado de uma chave (digamos kj329nf982bc9wn1), a ferramenta fornecerá um texto criptografado de:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Se desejar, você pode converter a chave e o texto cifrado em binário e comparar como o texto cifrado do primeiro bloco alinha-se com todo o processo descrito.

Descriptografia DES

No DES, o processo de descriptografia é incrivelmente simples. A estrutura Feistel do algoritmo permite que seja facilmente revertida. O processo é executado quase exatamente o mesmo para descriptografar informações. A única diferença é que as subchaves são aplicadas ao contrário. Essa é uma configuração eficiente, porque significa que o mesmo software e hardware podem ser usados ​​nos processos de criptografia e descriptografia.

Para descriptografar os dados, ele primeiro passa por uma permutação inicial, depois o bloco é dividido e a metade direita passa pela função F. A diferença é que, na primeira rodada de descriptografia, a 16ª subchave é aplicada. Tudo o resto acontece normalmente. Quando a função F é concluída, ela é XORed com o lado esquerdo do bloco.

Os blocos são trocados e o resultado passa pelo mesmo processo para a segunda rodada, com a única exceção que a 15ª subchave é aplicada. Esse processo continua até a 16ª rodada, quando a 1ª subchave é usada.

Assim como no processo de criptografia, os blocos não são trocados no estágio final e os dados passam por uma permutação final. Isso finaliza o processo de descriptografia, resultando no texto original da mensagem.

3DES

À medida que as fraquezas de segurança do DES se tornaram mais aparentes, o 3DES foi proposto como uma maneira de estender seu tamanho de chave sem precisar criar um algoritmo inteiramente novo. Em vez de usar uma única chave como no DES, o 3DES executa o algoritmo DES três vezes, com três chaves de 56 bits:

• A chave um é usada para criptografar o texto simples.
• A chave dois é usada para decifrar o texto que foi criptografado pela chave um.
• A chave três é usada para criptografar o texto que foi decifrado pela chave três.

Em cada estágio, o processo completo de DES é seguido conforme descrito acima.

Agora, você pode estar se perguntando “Como a aplicação de descriptografia na segunda etapa aumenta a segurança?”

A resposta é que ele usa uma chave separada. Se a primeira chave também foi usada para descriptografar os dados na segunda etapa, os dados voltariam ao ponto em que começaram.

No entanto, como usa uma chave diferente, o processo de descriptografia não serve para descriptografar os dados. Pode parecer logicamente perverso, mas descriptografar com uma chave separada serve apenas para misturar os dados ainda mais.

Depois que a segunda chave “descriptografa” os dados, a terceira chave é aplicada para criptografá-los novamente. O resultado é o texto cifrado em 3DES.

O 3DES está estruturado dessa maneira porque permite que as implementações sejam compatíveis com o DES de chave única, o DES de duas chaves e o DES de três chaves (estes são abordados na seção a seguir). Isso não funcionaria se a criptografia fosse usada nas três etapas.

Opções de codificação 3DES

Tecnicamente, o 3DES pode ser implementado com três configurações de chave diferentes. Apesar disso, a segunda e a terceira opção são inseguras e nunca devem ser implementadas.

• Opção 1 de digitação – Esta opção usa três chaves independentes e é a mais segura.
• Opção de chave dois – Nesta configuração, a primeira e a terceira chaves são as mesmas.
• Opção de digitação três – Isso usa três chaves idênticas. Quando chaves idênticas são usadas, o processo de descriptografia no segundo estágio cancela a primeira criptografia, deixando apenas a criptografia final para alterar os dados. Isso torna o resultado o igual ao DES comum.

O processo 3DES: digitando a opção um

Sejamos honestos, todo o processo do 3DES pode fazer sua cabeça girar, especialmente se você não conhece a criptografia. Para ajudá-lo a entender, aqui está um breve resumo de todo o esquema de criptografia do algoritmo 3DES:

O texto simples entra no algoritmo 3DES e é o primeiro criptografado com a chave um nas seguintes etapas:

• • Programação de chaves – as 16 subchaves são derivadas da chave um

  • Permutação inicial

  • O bloco é dividido em metades esquerda e direita

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave da rodada

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Tornar o antigo lado direito o novo lado esquerdo e o resultado o novo lado direito

      Repita as etapas acima 14 vezes

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave para a 16ª rodada

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Combine os lados esquerdo e direito do bloco

• • Permutação final

Pegue o texto que foi criptografado com a chave um e envie-o através do Processo de “descriptografia” com chave dois:

• • Programação de chaves – as 16 subchaves são derivadas da chave dois

  • Permutação inicial

  • O bloco é dividido em metades esquerda e direita

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave da rodada (a partir da 16ª subchave para descriptografia)

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Tornar o antigo lado direito o novo lado esquerdo e o resultado o novo lado direito

      Repita as etapas acima 14 vezes

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave da primeira rodada

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Combine os lados esquerdo e direito do bloco
  • Permutação final

Pegue os dados que foram “descriptografados” pela chave dois e envie-os através do enprocesso de criptografia com chave três:

• • Programação de chaves – as 16 subchaves são derivadas da chave três

  • Permutação inicial

  • O bloco é dividido em metades esquerda e direita

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave da rodada

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Tornar o antigo lado direito o novo lado esquerdo e o resultado o novo lado direito

      Repita as etapas acima 14 vezes

• • • A metade direita é enviada através da função F

      • Permutação de expansão

      • XOR com a subchave para a 16ª rodada

      • Substituição

      • Permutação

    • XOR o resultado da função F com o lado esquerdo

    • Combine os lados esquerdo e direito do bloco

• • Permutação final

O resultado é o texto cifrado em 3DES.

A segurança do 3DES

A segurança do 3DES depende de qual opção de codificação está sendo usada. A opção de digitação 1 envolve três chaves diferentes de 56 bits, o que fornece um comprimento total de 168 bits. O tamanho efetivo é reduzido consideravelmente por ataques meet-in-the-middle, que reduzem sua segurança no mundo real a 112 bits.

Os ataques Meet-in-the-middle são úteis contra esquemas de criptografia que repetem o mesmo algoritmo várias vezes. A técnica armazena os valores imediatos de cada estágio de criptografia e usa essas informações para melhorar radicalmente o tempo necessário para a força bruta do algoritmo..

As opções dois e três têm chaves significativamente menores e são vulneráveis ​​a ataques de texto simples conhecido e ataques de texto simples escolhido, além de outros.

Os ataques de texto sem formatação conhecidos são possíveis quando um adversário tem acesso ao texto sem formatação e ao texto cifrado de uma mensagem. Se um algoritmo é suscetível a esses ataques, o invasor pode usar essas informações para deduzir a chave, o que permite que ele decifre todos os outros dados que foram criptografados pela mesma chave.

Um ataque de texto simples escolhido é semelhante, mas envolve o invasor descobrindo a chave comparando textos cifrados com textos arbitrários.

Devido a essas vulnerabilidades e aos pequenos tamanhos gerais de chave envolvidos, as opções de codificação dois e três são inseguras e não devem ser implementadas.

O 3DES é seguro?

Como o 3DES será descontinuado nos próximos anos, é melhor usar outros algoritmos. Embora a opção de digitação ainda seja considerada segura para muitos aplicativos, não há muitos bons motivos para usá-lo em vez de uma alternativa como a AES.

Embora o 3DES ocupe um lugar importante na criptografia como acompanhamento do DES, seus anos de glória terminaram e é hora de seguir em frente. Se você deseja proteger seus sistemas no futuro, use um algoritmo mais atualizado.

Palavras-chave: Tipos de criptografia comuns explicados

Plano X pelo DoD licenciado sob CC0