O que é a troca de chaves Diffie – Hellman e como ela funciona?

A troca de chaves Diffie-Hellman foi um dos desenvolvimentos mais importantes em criptografia de chave pública e ainda é frequentemente implementado em diversos protocolos de segurança atuais.

Ele permite que duas partes que não se encontraram anteriormente estabeleçam com segurança uma chave que elas podem usar para proteger suas comunicações. Neste artigo, explicaremos para que é usado, como funciona passo a passo, suas diferentes variações, bem como as considerações de segurança que precisam ser observadas para implementá-lo com segurança.

O que é a troca de chaves Diffie-Hellman?

A troca de chaves Diffie-Hellman foi a primeiro método amplamente utilizado para desenvolver e trocar chaves com segurança em um canal inseguro.

Pode não parecer tão empolgante ou inovador nos termos acima, então vamos dar um exemplo que explica por que a troca de chaves Diffie-Hellman foi um marco tão importante no mundo da criptografia e por que ainda é usada com tanta frequência hoje.

Digamos que você seja um espião extremamente secreto e precise enviar algumas informações importantes para sua sede. Como você impediria que seus inimigos recebessem a mensagem?

A solução mais comum seria criptografar a mensagem com um código. A maneira mais fácil é organizar previamente qualquer tipo de código e chave que você planeja usar com antecedência ou fazê-lo em um canal de comunicação seguro.

Digamos que você seja um espião particularmente ruim e você e sua sede decidam usar uma cifra de turno fraca para codificar suas mensagens. Nesse código, todo “a” se torna “b”, todo “b” se torna “c”, todo “c” se torna “d” e assim por diante, até o “z” se tornar um “a”.

Sob essa cifra de turno, a mensagem “Vamos jantar” se torna “Não dá para curtir”. Felizmente, em nossa situação hipotética, seus adversários são tão incompetentes quanto você e são incapazes de decifrar um código tão simples, o que os impede de acessar o conteúdo da mensagem.

Mas o que acontece se você não conseguir organizar um código com seu destinatário antecipadamente?

Digamos que você queira se comunicar com um espião de uma nação aliada que você nunca conheceu antes. Você não tem um canal seguro para conversar com eles. Se você não criptografar sua mensagem, qualquer adversário que a intercepte poderá ler o conteúdo. Se você o criptografar sem informar o código ao aliado, o inimigo não poderá lê-lo, mas o aliado também não.

Esse problema foi um dos maiores enigmas da criptografia até a década de 1970:

Como você pode trocar informações com segurança com alguém, se não teve a oportunidade de compartilhar a chave com antecedência?

A troca de chaves Diffie-Hellman foi o primeiro mecanismo usado publicamente para resolver esse problema. O algoritmo permite que aqueles que nunca se conheceram criem com segurança uma chave compartilhada, mesmo em um canal inseguro que os adversários possam monitorar.

A história da troca de chaves Diffie-Hellman

A troca de chaves Diffie-Hellman tem suas raízes nos anos 70. Embora o campo da criptografia tenha se desenvolvido significativamente ao longo do século XX, esses avanços foram focados principalmente na área de criptografia de chave simétrica.

Não foi até 1976 que os algoritmos de chave pública surgiram na esfera pública, quando Whitfield Diffie e Martin Hellman publicaram seu artigo, Novas direções em criptografia. A colaboração descreveu os mecanismos por trás de um novo sistema, que viria a ser conhecido como Troca de chaves Diffie-Hellman.

O trabalho foi parcialmente inspirado por desenvolvimentos anteriores feitos por Ralph Merkle. O assim chamado Quebra-cabeças de Merkle envolva uma parte criando e enviando uma série de quebra-cabeças criptográficos para a outra. Esses quebra-cabeças exigiriam uma quantidade moderada de recursos computacionais para resolver.

O destinatário escolheria aleatoriamente um quebra-cabeça para resolver e depois gastaria o esforço necessário para concluí-lo. Depois que o quebra-cabeça é resolvido, um identificador e uma chave de sessão são revelados ao destinatário. O destinatário transmite o identificador de volta ao remetente original, o que permite que o remetente saiba qual quebra-cabeça foi resolvido.

Como o remetente original criou os quebra-cabeças, o identificador os informa sobre qual chave de sessão o destinatário descobriu e as duas partes podem usar essa chave para se comunicar com mais segurança. Se um invasor estiver ouvindo a interação, ele terá acesso a todos os quebra-cabeças, bem como ao identificador que o destinatário transmite de volta ao remetente original.

O identificador não informa ao invasor qual chave de sessão está sendo usada; portanto, a melhor abordagem para descriptografar as informações é: resolver todos os quebra-cabeças para descobrir a chave de sessão correta. Como o atacante terá que resolver metade dos quebra-cabeças em média, acaba sendo muito mais difícil descobrir a chave do que o destinatário.

Essa abordagem fornece mais segurança, mas está longe de ser uma solução perfeita. A troca de chaves Diffie-Hellman pegou algumas dessas idéias e as tornou mais complexas para criar um método seguro de criptografia de chave pública.

Embora tenha se tornado conhecida como troca de chaves Diffie-Hellman, Martin Hellman propôs que o algoritmo fosse denominado troca de chaves Diffie-Hellman-Merkle, para refletir o trabalho que Ralph Merkle colocou na criptografia de chave pública.

Pensa-se publicamente que Merkle, Hellman e Diffie foram as primeiras pessoas a desenvolver criptografia de chave pública até 1997, quando o governo britânico desclassificou o trabalho realizado no início dos anos 70 por James Ellis, Clifford Cox e Malcolm Williamson.

Acontece que o trio criou o primeiro esquema de criptografia de chave pública entre 1969 e 1973, mas seu trabalho foi classificado por duas décadas. Foi conduzido sob a Sede de Comunicação do Governo (GCHQ), uma agência de inteligência do Reino Unido.

Sua descoberta foi, na verdade, o algoritmo RSA, então Diffie, Hellman e Merkle ainda foram os primeiros a desenvolver a troca de chaves Diffie-Hellman, mas não mais os primeiros inventores da criptografia de chave pública.

Onde é usada a troca de chaves Diffie-Hellman?

O principal objetivo da troca de chaves Diffie-Hellman é desenvolver com segurança segredos compartilhados que possam ser usados ​​para derivar chaves. Essas chaves podem ser usadas com algoritmos de chave simétrica para transmitir informações de maneira protegida. Algoritmos simétricos tendem a ser usados ​​para criptografar a maior parte dos dados porque são mais eficientes que os algoritmos de chave pública.

Tecnicamente, a troca de chaves Diffie-Hellman pode ser usada para estabelecer chaves públicas e privadas. No entanto, na prática, o RSA tende a ser usado. Isso ocorre porque o algoritmo RSA também é capaz de assinar certificados de chave pública, enquanto a troca de chaves Diffie-Hellman não é.

O algoritmo ElGamal, que foi muito utilizado no PGP, baseia-se na troca de chaves Diffie-Hellman; portanto, qualquer protocolo que o utilize efetivamente implementa um tipo de Diffie-Hellman.

Como um dos métodos mais comuns para distribuir chaves com segurança, a troca de chaves Diffie-Hellman é freqüentemente implementado em protocolos de segurança como TLS, IPsec, SSH, PGP e muitos outros. Isso faz parte integrante de nossas comunicações seguras.

Como parte desses protocolos, a troca de chaves Diffie-Hellman é frequentemente usada para ajudar a proteger sua conexão com um site, acessar remotamente outro computador e enviar emails criptografados

Como funciona a troca de chaves Diffie-Hellman?

A troca de chaves Diffie-Hellman é complexa e pode ser difícil entender como funciona. Ele usa números muito grandes e muita matemática, algo que muitos de nós ainda tememos com essas longas e chatas aulas do ensino médio.

Para tornar as coisas um pouco mais fáceis de entender, começaremos explicando a troca de chaves Diffie-Hellman com uma analogia. Depois de ter uma ideia geral de como isso funciona, passaremos a uma descrição mais técnica dos processos subjacentes.

A melhor analogia para o esquema Diffie-Hellman é pensar em duas pessoas misturando tinta. Vamos usar o padrão de criptografia e dizer que seus nomes são Alice e Bob. Ambos concordam com uma cor aleatória para começar. Digamos que eles se enviem uma mensagem e decidir amarelo como sua cor comum, assim como no diagrama abaixo:

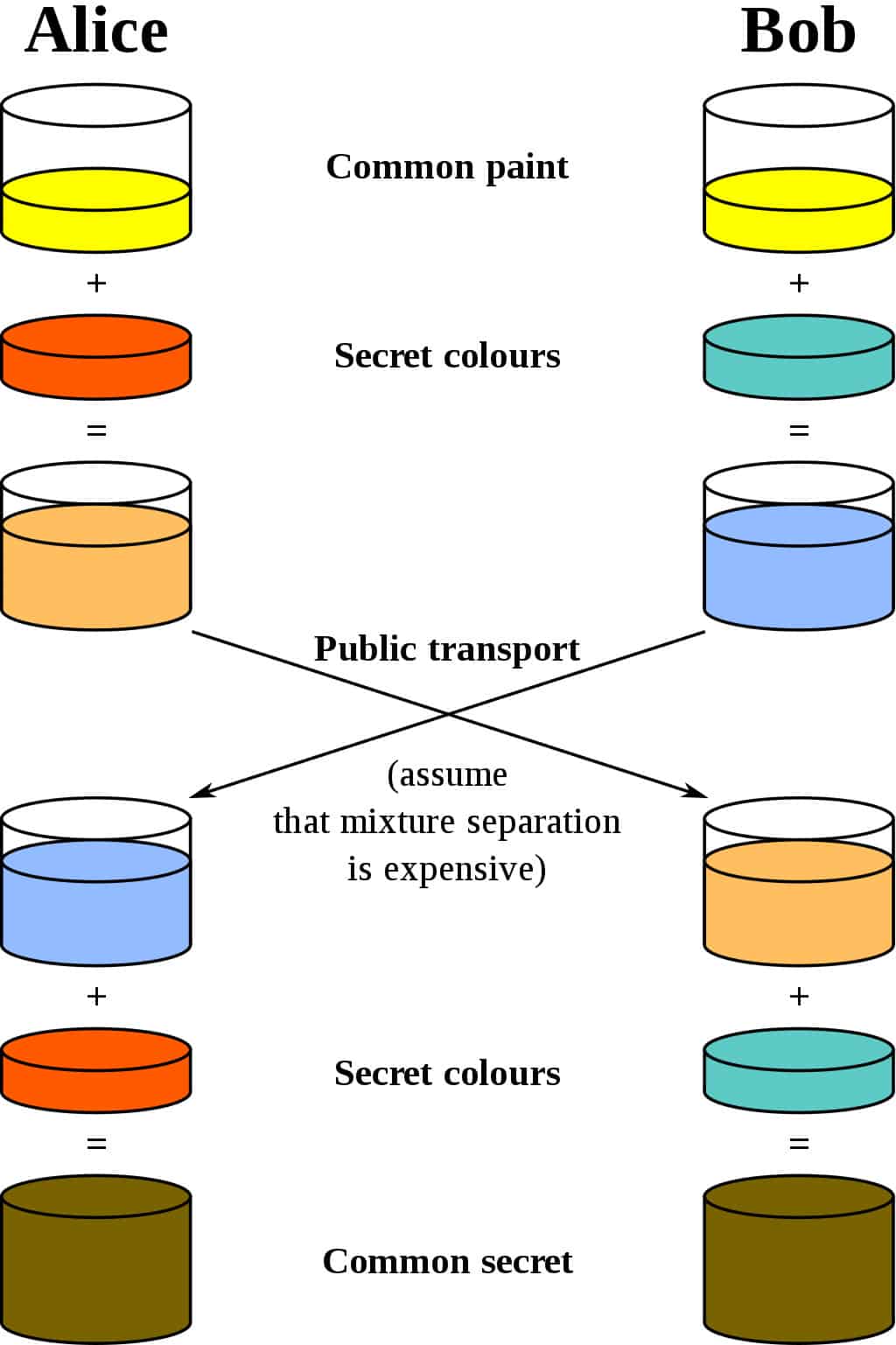
veja sua própria cor secreta. Eles não dizem à outra parte sua escolha. Digamos que Alice escolhe vermelho, enquanto Bob escolhe um azul ligeiramente esverdeado.

O próximo passo é que Alice e Bob misturem sua cor secreta (vermelho para Alice, azul esverdeado para Bob) com o amarelo com o qual eles concordaram mutuamente. De acordo com o diagrama, Alice acaba com um mistura alaranjada, enquanto o resultado de Bob é um azul mais profundo.

Depois de terminar a mixagem, eles enviam o resultado para a outra parte. Alice recebe o azul mais profundo, enquanto Bob recebe a tinta cor de laranja.

Depois de receberem o resultado misto do parceiro, eles adicionam sua cor secreta. Alice pega o azul mais profundo e adiciona sua tinta vermelha secreta, enquanto Bob adiciona seu azul esverdeado secreto à mistura de laranja que ele acabou de receber.

O resultado? Ambos saem com a mesma cor, que neste caso é um marrom nojento. Pode não ser o tipo de cor com o qual você deseja pintar sua sala, mas é uma cor compartilhada. Essa cor compartilhada é chamada de segredo comum.

A parte crítica da troca de chaves Diffie-Hellman é que ambas as partes terminam com o mesmo resultado, sem precisar enviar todo o segredo comum pelo canal de comunicação. Escolher uma cor comum, suas próprias cores secretas, trocar a mistura e, em seguida, adicionar sua própria cor mais uma vez, oferece a ambas as partes uma maneira de chegar ao mesmo segredo comum sem precisar enviar a coisa toda.

Se um invasor está ouvindo a troca, tudo o que ele pode acessar é a cor amarela comum com a qual Alice e Bob começam, bem como as cores misturadas que são trocadas. Como isso é realmente feito com números enormes, em vez de tinta, essas informações não são suficientes para o ataque discernir as cores secretas iniciais ou o segredo comum (tecnicamente, é possível calcular o segredo comum dessas informações, mas em uma implementação segura da troca de chaves Diffie-Hellman, levaria uma quantidade inviável de tempo e recursos computacionais para isso).

Essa estrutura da troca de chaves Diffie-Hellman é o que a torna tão útil. Ele permite que as duas partes se comuniquem através de uma conexão potencialmente perigosa e ainda apresentem um segredo compartilhado que elas podem usar para criar chaves de criptografia para suas futuras comunicações. Não importa se algum invasor está ouvindo, porque o segredo compartilhado completo nunca é enviado pela conexão.

Os detalhes técnicos da troca de chaves Diffie-Hellman

Hora de matemática …

Não se preocupe, vamos devagar e tentaremos tornar todo o processo o mais fácil de entender possível. Segue uma premissa semelhante à analogia mostrada acima, mas em vez de misturar e enviar cores, o esquema Diffie-Hellman efetivamente faz cálculos com base em números primos excepcionalmente grandes e os envia através.

Para garantir a segurança, é recomendável que o prime (p) tem pelo menos 2048 bits, que é o equivalente binário de um número decimal desse tamanho:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

Para evitar que a cabeça de alguém exploda, executaremos essa explicação com números muito menores. Esteja ciente que a troca de chaves Diffie-Hellman seria insegura se usasse números tão pequenos quanto os do nosso exemplo. Estamos apenas usando números tão pequenos para demonstrar o conceito de uma maneira mais simples.

Na forma mais básica da troca de chaves Diffie-Hellman, Alice e Bob começam decidindo mutuamente dois números para começar, em oposição à única tinta comum no exemplo acima. Esses são o módulo (p) e a base (g).

Em uso prático, o módulo (p) é um número primo muito grande, enquanto a base (g) é relativamente pequeno para simplificar os cálculos. A base (g) é derivado de um grupo cíclico (G) que normalmente é gerado bem antes que as outras etapas ocorram.

Para o nosso exemplo, digamos que o módulo (p) é 17, enquanto a base (g) é 4.

Depois que eles decidem mutuamente sobre esses números, Alice decide um número secreto (uma), enquanto Bob escolhe seu próprio número secreto (b) Digamos que eles escolham:

a = 3

b = 6

Alice então executa o seguinte cálculo para fornecer a ela o número que ela enviará a Bob:

A = ga mod p

No cálculo acima, mod significa uma operação de módulo. Estes são essencialmente cálculos para descobrir o restante depois de dividir o lado esquerdo pelo direito. Como um exemplo:

15 mod 4 = 3

Se você entender como as operações do módulo funcionam, você poderá executá-las nos cálculos a seguir, caso contrário, poderá usar uma calculadora on-line..

Então, vamos colocar nossos números na fórmula:

A = 43 mod 17

A = 64 mod 17

A = 13

Quando fazemos o mesmo com Bob, obtemos:

B = 46 mod 17

B = 4096 mod 17

B = 16

Alice então envia seu resultado (UMA) para Bob, enquanto Bob envia sua figura (B) para Alice. Alice então calcula o segredo compartilhado (s) usando o número que ela recebeu de Bob (B) e seu número secreto (uma), usando a seguinte fórmula:

s = Ba mod p

s = 163 mod 17

s = 4.096 mod 17

s = 16

Bob então executa o que é essencialmente o mesmo cálculo, mas com o número que Alice enviou a ele (UMA), bem como o seu próprio número secreto (b):

s = UMAb mod p

s = 136 mod 17

s = 4.826.809 mod 17

s = 16

Como você pode ver, ambas as partes terminaram com o mesmo resultado para s, 16. Esse é o segredo compartilhado, que apenas Alice e Bob conhecem. Eles podem usar isso para configurar uma chave para criptografia simétrica, permitindo que eles enviem informações com segurança entre si de uma maneira que somente eles possam acessá-la.

Observe que, embora B e s são os mesmos no exemplo acima, isso é apenas uma coincidência com base nos pequenos números que foram escolhidos para esta ilustração. Normalmente, esses valores não seriam os mesmos em uma implementação real da troca de chaves Diffie-Hellman.

Embora muitos dos dados acima sejam enviados pelo canal em texto não criptografado (p, g, A e B) e pode ser lido por possíveis invasores, o segredo compartilhado (s) nunca é transmitido. Não seria prático para um invasor calcular o segredo compartilhado (s) ou um dos números secretos (uma e b) das informações enviadas em texto não criptografado.

Obviamente, isso pressupõe que a troca de chaves Diffie-Hellman seja implementada adequadamente e que sejam usados ​​números suficientemente grandes. Enquanto essas disposições forem respeitadas, a troca de chaves Diffie-Hellman é considerada uma maneira segura de estabelecer um segredo compartilhado que pode ser usado para proteger futuras comunicações.

Estabelecendo uma chave compartilhada entre várias partes

A troca de chaves Diffie-Hellman também pode ser usada para configurar uma chave compartilhada com um número maior de participantes. Funciona da mesma maneira, exceto que outras rodadas dos cálculos são necessárias para que cada parte adicione seu número secreto e termine com o mesmo segredo compartilhado.

Assim como na versão de duas partes da troca de chaves Diffie-Hellman, algumas partes da informação são enviadas por canais inseguros, mas não o suficiente para que um invasor possa calcular o segredo compartilhado.

Por que a troca de chaves Diffie-Hellman é segura?

Em nível matemático, a troca de chaves Diffie-Hellman conta com funções unidirecionais como base para sua segurança. Estes são cálculos que são simples de serem feitos de uma maneira, mas muito mais difíceis de calcular ao contrário.

Mais especificamente, ele se baseia no problema de Diffie-Hellman, que pressupõe que, sob os parâmetros corretos, é inviável calcular gab dos valores separados de g, guma e gb. Atualmente, não existe uma maneira conhecida publicamente de encontrar facilmente gab dos outros valores, e é por isso que a troca de chaves Diffie-Hellman é considerada segura, apesar de os invasores poderem interceptar os valores p, g, UMA, e B.

Autenticação & a troca de chaves Diffie-Hellman

No mundo real, a troca de chaves Diffie-Hellman raramente é usada por si só. A principal razão por trás disso é que ele não fornece autenticação, o que deixa os usuários vulneráveis ​​a ataques do tipo intermediário.

Esses ataques podem ocorrer quando a troca de chaves Diffie-Hellman é implementada por si só, porque não tem como verificar se a outra parte em uma conexão é realmente quem eles dizem que são. Sem qualquer forma de autenticação, os usuários podem realmente estar se conectando com atacantes quando eles pensam que estão se comunicando com uma parte confiável.

Por esse motivo, a troca de chaves Diffie-Hellman geralmente é implementada juntamente com alguns meios de autenticação. Isso geralmente envolve o uso de certificados digitais e um algoritmo de chave pública, como o RSA, para verificar a identidade de cada parte.

Variações da troca de chaves Diffie-Hellman

A troca de chaves Diffie-Hellman pode ser implementada de várias maneiras diferentes e também forneceu a base para vários outros algoritmos. Algumas dessas implementações fornecem autorização, enquanto outras possuem vários recursos criptográficos, como sigilo direto perfeito.

Curva elíptica Diffie-Hellman

Curva elíptica Diffie-Hellman tira proveito da estrutura algébrica das curvas elípticas para permitir que suas implementações atinjam um nível de segurança semelhante com um tamanho de chave menor. Uma chave de curva elíptica de 224 bits fornece o mesmo nível de segurança que uma chave RSA de 2048 bits. Isso pode tornar as trocas mais eficientes e reduzir os requisitos de armazenamento.

Além do menor tamanho da chave e do fato de depender das propriedades das curvas elípticas, a Diffie-Hellman de curva elíptica opera de maneira semelhante à troca de chaves Diffie-Hellman padrão.

TLS   

O TLS, que é um protocolo usado para proteger grande parte da Internet, pode usar a troca Diffie-Hellman de três maneiras diferentes: anônima, estática e efêmera. Na prática, apenas Diffie-Hellman efêmero deve ser implementado, porque as outras opções têm problemas de segurança.

• Diffie-Hellman anônimo – Esta versão da troca de chaves Diffie-Hellman não usa autenticação, deixando-a vulnerável a ataques intermediários. Não deve ser usado ou implementado.
• Diffie-Hellman estático – Static Diffie-Hellman usa certificados para autenticar o servidor. Por padrão, não autentica o cliente nem fornece sigilo para a frente.
• Diffie-Hellman efêmero – Essa é considerada a implementação mais segura porque fornece sigilo direto perfeito. Geralmente é combinado com um algoritmo como DSA ou RSA para autenticar uma ou ambas as partes na conexão. O efêmero Diffie-Hellman usa pares de chaves diferentes cada vez que o protocolo é executado. Isso confere à conexão um sigilo de encaminhamento perfeito, pois mesmo que uma chave seja comprometida no futuro, ela não poderá ser usada para descriptografar todas as mensagens anteriores.

ElGamal

ElGamal é um algoritmo de chave pública criado sobre a troca de chaves Diffie-Hellman. Como a Diffie-Hellman, ela não contém provisões para autenticação por si só e geralmente é combinada com outros mecanismos para esse fim..

O ElGamal foi usado principalmente em PGP, GNU Privacy Guard e outros sistemas porque seu principal rival, RSA, foi patenteado. A patente da RSA expirou em 2000, o que permitiu sua implementação livremente após essa data. Desde então, ElGamal não tem sido implementado com tanta frequência.

STS

O protocolo Estação a Estação (STS) também se baseia na troca de chaves Diffie-Hellman. É outro esquema de contrato importante, no entanto, fornece proteção contra ataques do tipo intermediário, além de sigilo direto perfeito.

Requer que ambas as partes na conexão já tenham um par de chaves, usado para autenticar cada lado. Se as partes ainda não se conhecem, os certificados podem ser usados ​​para validar as identidades de ambas as partes..

A troca de chaves Diffie-Hellman & RSA

Como discutimos anteriormente, a troca de chaves Diffie-Hellman é frequentemente implementada ao lado do RSA ou de outros algoritmos para fornecer autenticação para a conexão. Se você conhece o RSA, pode estar se perguntando por que alguém se incomodaria em usar a troca de chaves Diffie-Hellman também, pois o RSA permite que as partes que nunca se conheceram se comuniquem.

A RSA permite que seus usuários criptografem mensagens com a chave pública do correspondente, para que possam ser descriptografados apenas pela chave privada correspondente. No entanto, na prática, O RSA não é usado para criptografar a totalidade das comunicações – isso seria muito ineficiente.

Em vez disso, o RSA geralmente é usado apenas como um meio para autenticar ambas as partes. Faz isso com os certificados digitais de cada parte, que serão verificados por uma autoridade de certificação para provar que um proprietário de certificado é realmente quem eles dizem ser e que a chave pública no certificado realmente pertence a eles.

Para autenticação mútua, cada parte assinará uma mensagem usando sua chave privada e a enviará ao parceiro de comunicação. Cada destinatário pode então verifique a identidade da outra parte verificando as mensagens assinadas em relação à chave pública no certificado digital do parceiro de comunicação (consulte o artigo acima mencionado no RSA para obter mais detalhes sobre como isso funciona, particularmente o Assinando mensagens seção).

Agora que as duas partes foram autenticadas, é tecnicamente possível continuar usando o RSA para enviar mensagens criptografadas com segurança entre si, no entanto, isso acabaria sendo ineficiente.

Para contornar essa ineficiência, muitos protocolos de segurança usam um algoritmo como a troca de chaves Diffie-Hellman para criar um segredo comum que pode ser usado para estabelecer uma chave simétrica compartilhada. Essa chave simétrica é usada em um algoritmo de chave simétrica, como o AES, para criptografar os dados que as duas partes pretendem enviar com segurança entre si.

Pode parecer um processo complexo e complicado, mas acaba sendo muito mais rápido e menos exigente em recursos quando comparado ao uso de um algoritmo de chave pública para toda a troca. Isto é porque a criptografia de chave simétrica é uma ordem de magnitude mais eficiente que a criptografia de chave pública.

Além das ineficiências que acabamos de mencionar, existem outras desvantagens decorrentes do uso exclusivo do RSA. A RSA precisa de preenchimento para torná-la segura, portanto, um algoritmo adicional precisaria ser implementado adequadamente ao lado dele para torná-lo seguro.

A RSA não fornece sigilo direto perfeito, também, o que é outra desvantagem quando comparado à efêmera troca de chaves Diffie-Hellman. Coletivamente, esses motivos são os motivos pelos quais, em muitas situações, é melhor aplicar apenas o RSA em conjunto com a troca de chaves Diffie-Hellman.

Como alternativa, a troca de chaves Diffie-Hellman pode ser combinada com um algoritmo como o DSS (Digital Signature Standard) para fornecer autenticação, troca de chaves, confidencialidade e verificar a integridade dos dados. Em tal situação, o RSA não é necessário para proteger a conexão.

Questões de segurança da troca de chaves Diffie-Hellman

A segurança da troca de chaves Diffie-Hellman depende de como ela é implementada, bem como dos números escolhidos para ela. Como dissemos acima, ele não tem como autenticar a outra parte por si só, mas, na prática, outros mecanismos são usados ​​para garantir que a outra parte em uma conexão não seja um impostor.

Parâmetros para seleção de número

Se uma implementação do mundo real da troca de chaves Diffie-Hellman usasse números tão pequenos quanto os do nosso exemplo, isso tornaria o processo de troca trivial para um invasor quebrar. Mas não é apenas o tamanho dos números que importa – os números também precisam ser suficientemente aleatórios. Se um gerador de números aleatórios produz uma saída previsível, pode minar completamente a segurança da troca de chaves Diffie-Hellman.

O número p deve ter 2048 bits para garantir a segurança. A base, g, pode ser um número relativamente pequeno como 2, mas precisa vir de uma ordem de G que tem um grande fator primo

O ataque Logjam

A troca de chaves Diffie-Hellman foi projetada com base no difícil problema de logaritmo discreto. O mecanismo publicamente conhecido mais eficaz para encontrar a solução é o algoritmo de peneira de campo numérico.

Os recursos desse algoritmo foram levados em consideração quando a troca de chaves Diffie-Hellman foi projetada. Em 1992, sabia-se que para um determinado grupo, G, três das quatro etapas envolvidas no algoritmo poderiam ser potencialmente calculadas antecipadamente. Se esse progresso foi salvo, a etapa final pode ser calculada em um tempo comparativamente curto.

Isso não era muito preocupante até que se percebesse que uma parcela significativa do tráfego da Internet usa os mesmos grupos de 1024 bits ou menos. Em 2015, uma equipe acadêmica executou os cálculos do primo mais comum de 512 bits usado pela troca de chaves Diffie-Hellman no TLS.

Eles também conseguiram fazer o downgrade de 80% dos servidores TLS compatíveis com DHE-EXPORT, para que aceitassem uma troca de chaves Diffie-Hellman de nível de exportação de 512 bits para a conexão. Isso significa que cada um desses servidores é vulnerável a um ataque de um adversário com bons recursos.

Os pesquisadores continuaram extrapolando seus resultados, estimando que um Estado-nação poderia quebrar um pico de 1024 bits. Ao quebrar o único prime de 1024 bits mais usado, a equipe acadêmica estimou que um adversário poderia monitorar 18% dos um milhão de sites HTTPS mais populares.

Eles continuaram dizendo que um segundo prime permitiria ao adversário descriptografar as conexões de 66% dos servidores VPN e 26% dos servidores SSH. Posteriormente no relatório, os acadêmicos sugeriram que a NSA já pode ter esses recursos.

“Uma leitura atenta dos vazamentos publicados pela NSA mostra que os ataques da agência às VPNs são consistentes com a obtenção de tal interrupção”.

Apesar dessa vulnerabilidade, a troca de chaves Diffie-Hellman ainda pode ser segura se for implementada corretamente. Enquanto uma chave de 2048 bits for usada, o ataque do Logjam não funcionará. Navegadores atualizados também são seguros contra esse ataque.

A troca de chaves Diffie-Hellman é segura?

Embora a troca de chaves Diffie-Hellman possa parecer complexa, é uma parte fundamental da troca segura de dados online. Desde que seja implementado juntamente com um método de autenticação apropriado e os números tenham sido selecionados corretamente, não será considerado vulnerável a ataques.

A troca de chaves Diffie-Hellman foi um método inovador para ajudar duas partes desconhecidas a se comunicarem com segurança quando foi desenvolvida na década de 1970. Embora agora implementemos versões mais recentes com chaves maiores para proteger contra a tecnologia moderna o próprio protocolo parece que continuará seguro até a chegada da computação quântica e os ataques avançados que virão com ele.

Tecnologia de negócios de segurança cibernética por TheDigitalArtist licenciado sob CC0