Qu’est-ce que le cryptage RSA et comment fonctionne-t-il?

Le cryptage RSA est un système qui résout ce qui était autrefois l’un des plus gros problèmes de cryptographie: Comment envoyer à quelqu’un un message codé sans avoir eu l’occasion de partager le code avec eux?

Cet article vous apprendra tout ce que vous devez savoir sur comment le cryptage RSA a été développé, Comment ça fonctionne, les mathématiques derrière, à quoi il sert ainsi que certains des les plus gros problèmes de sécurité auxquels il est confronté. L’apprentissage de RSA vous donnera quelques connaissances fondamentales qui vous aideront à comprendre combien de parties de notre vie en ligne sont sécurisées.

Qu’est-ce que le chiffrement RSA?

Supposons que vous souhaitiez révéler un secret à votre ami. Si vous êtes juste à côté d’eux, vous pouvez simplement le murmurer. Si vous êtes de l’autre côté du pays, cela ne fonctionnera évidemment pas. Vous pouvez le noter et le leur envoyer par la poste, ou utiliser le téléphone, mais chacun de ces canaux de communication n’est pas sécurisé et toute personne suffisamment motivée pourrait facilement intercepter le message.

Si le secret était suffisamment important, vous ne prendriez pas le risque de le noter normalement – des espions ou un employé des postes voyous pourraient parcourir votre courrier. De même, quelqu’un pourrait toucher votre téléphone à votre insu et enregistrer chaque appel que vous faites.

Une solution pour empêcher les écoutes indiscrètes d’accéder au contenu des messages consiste à crypter. Cela signifie essentiellement ajouter un code au message qui le transforme en un désordre brouillé. Si votre code est suffisamment complexe, alors les seules personnes qui pourront accéder au message d’origine sont celles qui ont accès au code.

Si vous avez eu la chance de partager le code avec votre ami au préalable, alors chacun de vous peut envoyer un message crypté à tout moment, sachant que vous deux êtes les seuls à pouvoir lire le contenu du message. Mais que se passe-t-il si vous n’avez pas eu la chance de partager le code à l’avance?

C’est l’un des problèmes fondamentaux de la cryptographie, qui a été résolu par schémas de chiffrement à clé publique (également appelés chiffrement asymétrique) comme RSA.

Sous le cryptage RSA, les messages sont cryptés avec un code appelé Clé publique, qui peut être partagé ouvertement. En raison de certaines propriétés mathématiques distinctes de l’algorithme RSA, une fois qu’un message a été chiffré avec la clé publique, il ne peut être déchiffré que par une autre clé, connue sous le nom de clé privée. Chaque utilisateur RSA possède une paire de clés composée de ses clés publiques et privées. Comme son nom l’indique, la clé privée doit être gardée secrète.

Les schémas de chiffrement à clé publique diffèrent de chiffrement à clé symétrique, où le processus de chiffrement et de déchiffrement utilisent la même clé privée. Ces différences rendent le chiffrement des clés publiques comme RSA utile pour communiquer dans des situations où il n’y a eu aucune possibilité de distribuer des clés en toute sécurité au préalable.

Les algorithmes à clé symétrique ont leurs propres applications, telles que le cryptage des données pour un usage personnel, ou lorsqu’il existe des canaux sécurisés sur lesquels les clés privées peuvent être partagées..

Voir également: Cryptographie à clé publique

Où le cryptage RSA est-il utilisé?

Le chiffrement RSA est souvent utilisé dans combinaison avec d’autres schémas de cryptage, ou pour signatures numériques qui peut prouver l’authenticité et l’intégrité d’un message. Il n’est généralement pas utilisé pour chiffrer des messages ou des fichiers entiers, car il est moins efficace et plus gourmand en ressources que le chiffrement à clé symétrique.

Pour rendre les choses plus efficaces, un fichier sera généralement chiffré avec un algorithme à clé symétrique, puis la clé symétrique sera chiffrée avec le chiffrement RSA. Dans le cadre de ce processus, seule une entité ayant accès à la clé privée RSA pourra déchiffrer la clé symétrique.

Sans pouvoir accéder à la clé symétrique, le le fichier d’origine ne peut pas être déchiffré. Cette méthode peut être utilisée pour sécuriser les messages et les fichiers, sans prendre trop de temps ni consommer trop de ressources de calcul.

Le chiffrement RSA peut être utilisé dans un certain nombre de systèmes différents. Il peut être implémenté dans OpenSSL, wolfCrypt, cryptlib et un certain nombre d’autres bibliothèques cryptographiques.

En tant que l’un des premiers schémas de cryptage à clé publique largement utilisés, RSA a jeté les bases de la plupart de nos communications sécurisées. C’était traditionnellement utilisé dans TLS et était également l’algorithme original utilisé dans le cryptage PGP. RSA est toujours visible dans une gamme de navigateurs Web, de messagerie électronique, de VPN, de chat et d’autres canaux de communication.

RSA est également souvent utilisé pour établir des connexions sécurisées entre les clients VPN et les serveurs VPN. Sous des protocoles comme OpenVPN, les poignées de main TLS peuvent utiliser l’algorithme RSA pour échanger des clés et établir un canal sécurisé.

L’arrière-plan du chiffrement RSA

Comme nous l’avons mentionné au début de cet article, avant le chiffrement à clé publique, il était difficile de communiquer en toute sécurité s’il n’y avait pas eu la possibilité d’échanger des clés en toute sécurité au préalable. S’il n’y avait pas la possibilité de partager le code à l’avance, ou un canal sécurisé par lequel les clés pourraient être distribuées, il n’y avait aucun moyen de communiquer sans la menace d’ennemis pouvant intercepter et accéder au contenu du message.

Ce n’est que dans les années 1970 que les choses ont vraiment commencé à changer. Le premier développement majeur vers ce que nous appelons maintenant la cryptographie à clé publique a été publié au début de la décennie par James H. Ellis. Ellis n’a pas pu trouver un moyen de mettre en œuvre son travail, mais il a été développé par son collègue Clifford Cocks pour devenir ce que nous connaissons maintenant sous le nom de Cryptage RSA.

La dernière pièce du puzzle est ce que nous appelons maintenant Échange de clés Diffie-Hellman. Malcolm J. Williamson, un autre collègue, a trouvé un système qui permettait à deux parties de partager une clé de chiffrement, même si le canal était surveillé par des adversaires.

Tous ces travaux ont été entrepris à l’agence britannique de renseignement, le Government Communications Headquarters (GCHQ), qui gardé la découverte classée. En partie à cause des limitations technologiques, le GCHQ ne pouvait pas voir une utilisation pour la cryptographie à clé publique à l’époque, donc le développement restait inactif sur l’étagère rassemblant la poussière. Ce n’est qu’en 1997 que l’œuvre a été déclassifiée et que les inventeurs originaux de RSA ont été reconnus.

Plusieurs années plus tard, des concepts similaires commençaient à se développer dans la sphère publique. Ralph Merkle a créé une première forme de cryptographie à clé publique, qui a influencé Whitfield Diffie et Martin Hellman dans la conception de l’échange de clés Diffie-Hellman.

Il manquait aux idées de Diffie et Hellman un aspect important qui ferait de leur travail une base de la cryptographie à clé publique. Ce fut un fonction unidirectionnelle difficile à inverser. En 1977, Ron Rivest, Adi Shamir et Leonard Adleman, dont les noms de famille forment l’acronyme RSA, a trouvé une solution après un an de travail sur le problème.

Les universitaires du MIT ont fait leur percée après une fête de la Pâque en 1977. Après une nuit de boisson, Rivest est rentré chez lui, mais au lieu de dormir, il a passé la soirée à écrire fiévreusement un document qui formalisait son idée de la fonction à sens unique nécessaire.

L’idée a été brevetée en 1983 par le MIT, mais ce n’est qu’au tout début d’Internet que l’algorithme RSA a commencé à voir l’adoption généralisée comme un outil de sécurité important..

Comment fonctionne le cryptage RSA?

Ce qui suit va être un peu une simplification, car trop de lecteurs ont probablement été marqués par leur professeur de mathématiques du secondaire. Pour éviter que les calculs ne deviennent trop incontrôlables, nous simplifier certains concepts et utiliser des nombres beaucoup plus petits. En réalité, le chiffrement RSA utilise des nombres premiers qui sont beaucoup plus importants et il existe quelques autres complexités.

Il y a plusieurs concepts différents que vous devrez maîtriser avant que nous puissions expliquer comment tout cela s’assemble. Ceux-ci inclus fonctions de trappe, générant des nombres premiers, fonction totient de Carmichael et les processus distincts impliqués dans calcul des clés publiques et privées utilisé dans les processus de chiffrement et de déchiffrement.

Fonctions de trappe

Le chiffrement RSA fonctionne en supposant que l’algorithme est facile à calculer dans une direction, mais presque impossible à l’envers. Par exemple, si on vous disait que 701.111 est un produit de deux nombres premiers, seriez-vous en mesure de déterminer quels sont ces deux nombres?

Même avec une calculatrice ou un ordinateur, la plupart d’entre nous n’auraient aucune idée de par où commencer, et encore moins de pouvoir trouver la réponse. Mais si nous inversons les choses, cela devient beaucoup plus facile. Quel est le résultat de:

907 x 773

Si vous vous ennuyiez assez, vous auriez pu sortir votre téléphone ou peut-être le calculer dans votre tête pour découvrir que la réponse est le 701.111 mentionné précédemment. Ces 907 et 773 sont les nombres premiers qui répondent à notre première question, ce qui nous montre que certaines équations peuvent être faciles à comprendre dans un sens, mais apparemment impossible à l’envers.

Un autre aspect intéressant de cette équation est qu’il est simple de déterminer l’un des nombres premiers si vous avez déjà l’autre, ainsi que le produit. Si on vous dit que 701.111 est le résultat de 907 multiplié par un autre nombre premier, vous pouvez le calculer l’autre premier avec l’équation suivante:

701.111 ÷ 907 = 773

Étant donné que la relation entre ces nombres est simple à calculer dans une direction, mais incroyablement difficile à inverser, l’équation est connue sous le nom de fonction de trappe. Sachez que bien que l’exemple ci-dessus soit difficile à comprendre, les ordinateurs peuvent effectuer l’opération en un temps insignifiant.

Pour cette raison, RSA utilise des nombres beaucoup plus importants. La taille des nombres premiers dans une implémentation RSA réelle varie, mais dans RSA 2048 bits, ils se réuniraient pour créer des clés de 617 chiffres. Pour vous aider à le visualiser, une clé serait un nombre de cette taille:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Génération de nombres premiers

Les fonctions de trappe mentionnées ci-dessus forment la base du fonctionnement des schémas de cryptage à clé publique et privée. Leurs propriétés permettent de partager des clés publiques sans mettre en danger le message ou révéler la clé privée. Ils permettent également de chiffrer les données avec une clé d’une manière qui ne peut être déchiffrée que par l’autre clé de la paire.

La première étape du chiffrement d’un message avec RSA consiste à générer les clés. Pour ce faire, nous avons besoin deux nombres premiers (p et q) qui sont sélectionnés avec un test de primalité. Un test de primalité est un algorithme qui trouve efficacement des nombres premiers, comme le test de primalité de Rabin-Miller.

Les nombres premiers dans RSA doivent être très grands et également relativement éloignés. Les nombres plus petits ou plus rapprochés sont beaucoup plus faciles à déchiffrer. Malgré cela, notre exemple utilisera des nombres plus petits pour rendre les choses plus faciles à suivre et à calculer.

Supposons que le test de primalité nous donne les nombres premiers que nous avons utilisés ci-dessus, 907 et 773. L’étape suivante consiste à découvrir le module (n), en utilisant la formule suivante:

n = p X q

Où p = 907 et q = 773

Donc:

n = 907 x 773

n = 701 111

Fonction totient de Carmichael

Une fois que nous avons n, nous utilisons Fonction totient de Carmichael:

    λ(n) = lcm (p – 1, q – 1)

Si cela fait un moment que vous n’avez pas utilisé les manuels de mathématiques, ce qui précède peut sembler un peu terrifiant. Vous pouvez ignorer cette partie et croire simplement que les calculs fonctionnent, sinon restez avec nous pour quelques calculs supplémentaires. Tout sera expliqué avec autant de détails que possible pour vous aider à vous familiariser avec les bases.

Pour ceux qui ne sont pas au courant, λ (n) représente le totient de Carmichael pour n, tandis que lcm signifie le plus petit commun multiple, qui est le nombre le plus bas que les deux p et q peut se diviser en. Il existe plusieurs façons de comprendre cela, mais le plus simple est de faire confiance à une calculatrice en ligne pour faire l’équation pour vous. Mettons donc nos chiffres dans l’équation:

    λ(701 111) = lcm (907 – 1, 773 – 1)

    λ(701 111) = lcm (906, 772)

   En utilisant la calculatrice liée ci-dessus, cela nous donne:

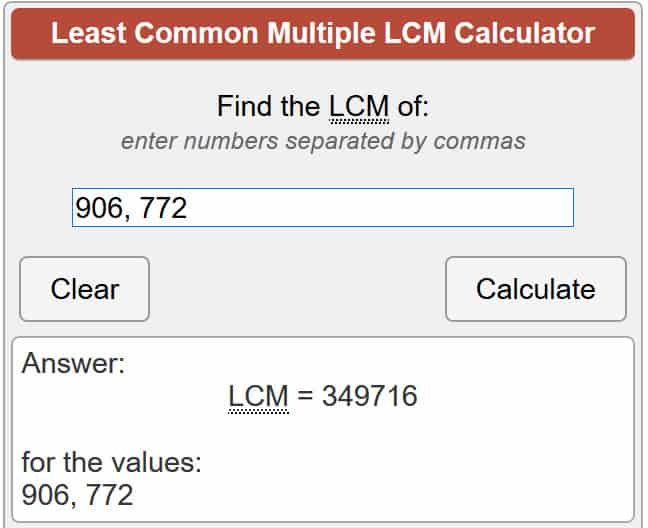
    λ(701 111) = 349 716

Génération de la clé publique

Maintenant que nous avons le totient de Carmichael de nos nombres premiers, c’est le temps de comprendre notre clé publique. Sous RSA, les clés publiques sont composées d’un nombre premier e, aussi bien que n. Le nombre e peut être compris entre 1 et la valeur de λ(n), qui dans notre exemple est 349 716.

Parce que la clé publique est partagée ouvertement, ce n’est pas si important pour e être un nombre aléatoire. En pratique, e est généralement fixé à 65,537, car lorsque des nombres beaucoup plus grands sont choisis au hasard, cela rend le chiffrement beaucoup moins efficace. Pour l’exemple d’aujourd’hui, nous allons garder les nombres petits pour rendre les calculs efficaces. Disons:

e = 11

Nos données chiffrées finales s’appellent le texte chiffré (c). Nous le tirons de notre message en clair (m), en appliquant la clé publique avec la formule suivante:

c = me mod n

Nous avons déjà trouvé e et nous savons n ainsi que. La seule chose que nous devons expliquer est mod. C’est un peu hors de la profondeur de cet article, mais il fait référence à un fonctionnement modulo, ce qui signifie essentiellement le reste qui reste lorsque vous divisez un côté par l’autre. Par exemple:

dix mod 3 = 1

C’est parce que 3 va dans 10 trois fois, avec un reste de 1.

Revenons à notre équation. Pour simplifier les choses, disons que le message (m) que nous voulons chiffrer et garder secret n’est qu’un numéro unique, 4. Branchez tout:

c = me mod n

c = 411 mod 701 111

c = 4 194 304 mod 701 111

Encore une fois, pour faire fonctionnement modulo facile, nous utiliserons une calculatrice en ligne, mais vous pouvez le découvrir par vous-même. En entrant 4194304 dans la calculatrice en ligne, il nous donne:

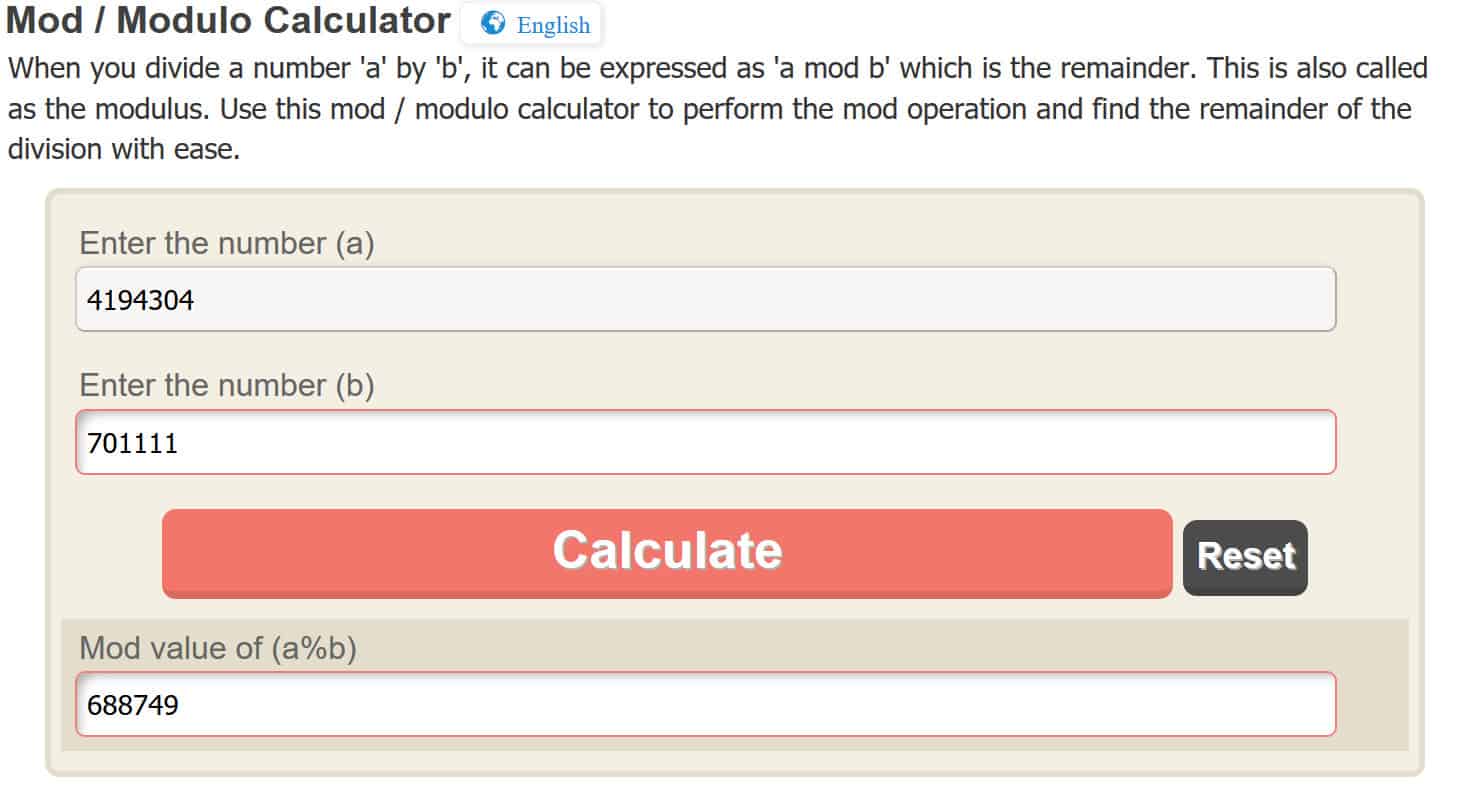
c = 688 749

Par conséquent, lorsque nous utilisons RSA pour crypter notre message, 4, avec notre clé publique, il nous donne la texte chiffré de 688 749. Les étapes précédentes peuvent sembler un peu trop lourdes en mathématiques, mais il est important de répéter ce qui s’est réellement passé.

Nous avions un message de 4, que nous voulions garder secret. Nous lui avons appliqué une clé publique, ce qui nous a résultat chiffré de 688 749. Maintenant qu’il est crypté, nous pouvons envoyer le numéro 688 749 en toute sécurité au propriétaire de la paire de clés. Ils sont les seuls à pouvoir le décrypter avec leur clé privée. Quand ils le décrypteront, ils verront le message que nous envoyions vraiment, 4.

Génération de la clé privée

Dans le chiffrement RSA, une fois que les données ou un message ont été transformés en texte chiffré avec une clé publique, ils ne peuvent être déchiffrés que par la clé privée de la même paire de clés. Les clés privées sont composées de ré et n. Nous savons déjà n, et l’équation suivante est utilisée pour trouver ré:

ré = 1 /e mod λ(n)

dans le Génération de la clé publique section ci-dessus, nous avons déjà décidé que dans notre exemple, e serait égal à 11. De même, nous savons que λ(n) équivaut à 349 716 de nos travaux antérieurs sous Fonction totient de Carmichael. Les choses deviennent un peu plus compliquées lorsque nous rencontrons cette section de la formule:

1/e mod

Cette équation peut sembler vous demander de diviser 1 par 11, mais ce n’est pas le cas. Au lieu de cela, cela symbolise simplement que nous devons calculer la inverse modulaire de e (qui dans ce cas est 11) et λ(n) (qui dans ce cas est 349 716).

Cela signifie essentiellement que au lieu d’effectuer une opération modulo standard, nous utiliserons plutôt l’inverse. Cela se trouve normalement avec l’algorithme euclidien étendu, mais c’est un peu en dehors de la portée de cet article, nous allons donc simplement tricher et utiliser une calculatrice en ligne à la place. Maintenant que nous comprenons tout ce qui se passe, insérons nos informations dans la formule:

ré = 1 /11 mod 349 716

Pour effectuer cette opération, entrez simplement 11 (ou toute valeur que vous pourriez avoir pour e si vous essayez cela avec votre propre exemple) où il est dit Entier et 349 716 (ou toute valeur que vous pourriez avoir pour λ(n) si vous essayez ceci avec votre propre exemple) où il est dit Modulo dans la calculatrice en ligne liée ci-dessus. Si vous l’avez fait correctement, vous devriez obtenir un résultat où:

ré = 254, 339

Maintenant que nous avons la valeur de ré, nous pouvons déchiffrer les messages qui ont été chiffrés avec notre clé publique en utilisant la formule suivante:

m = cré mod n

Nous pouvons maintenant revenir au texte chiffré que nous avons chiffré sous le Génération de la clé privée section. Lorsque nous avons chiffré le message avec la clé publique, cela nous a donné une valeur pour c sur 688 749. D’en haut, nous savons que ré vaut 254 339. Nous savons aussi que n est égal à 701 111. Cela nous donne:

m = 688 749254,339 mod 701 111.

Comme vous l’avez peut-être remarqué, essayer de porter un nombre à la 254 339e puissance peut être un peu trop pour la plupart des calculatrices normales. Au lieu de cela, nous utiliserons une calculatrice de décryptage RSA en ligne. Si vous vouliez utiliser une autre méthode, vous appliqueriez les pouvoirs comme vous le feriez normalement et effectueriez l’opération de module de la même manière que nous l’avons fait dans le Génération de la clé publique section.

Dans la calculatrice liée ci-dessus, entrez 701,111 où il est écrit Module d’alimentation: N, 254,399 où il est dit Clé de déchiffrement: D, et 688 749 où il est dit Message chiffré sous forme numérique, comme indiqué ci-dessous:

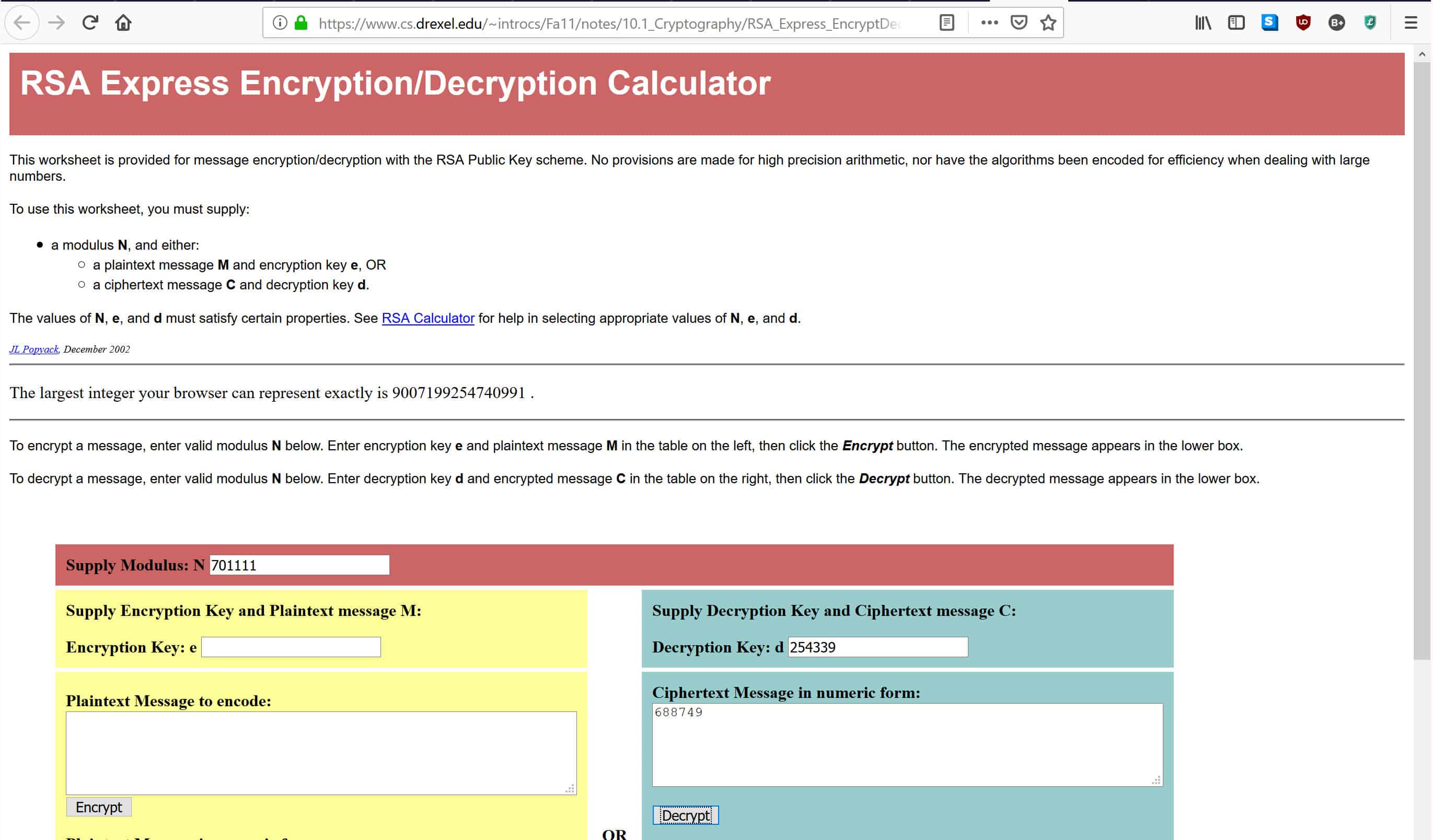
Une fois que vous avez entré les données, appuyez sur Déchiffrer, qui mettra les nombres à travers la formule de décryptage qui a été répertoriée ci-dessus. Cela vous donnera le message d’origine dans la case ci-dessous. Si vous avez tout fait correctement, vous devriez obtenir une réponse de 4, qui était le message original que nous avons chiffré avec notre clé publique.

Fonctionnement pratique du chiffrement RSA

Les sections ci-dessus devraient vous donner une compréhension raisonnable du fonctionnement du chiffrement derrière le chiffrement à clé publique. Cela peut être un peu déroutant, mais même ceux qui n’ont pas compris les subtilités des équations peuvent, espérons-le, retirer des informations importantes sur le processus..

Dans les étapes répertoriées ci-dessus, nous avons montré comment deux entités peuvent communiquer en toute sécurité sans avoir préalablement partagé un code au préalable. Tout d’abord, ils doivent chacun configurer leurs propres paires de clés et partager la clé publique entre eux. Les deux entités doivent garder leurs clés privées secrètes afin que leurs communications restent sécurisées.

Une fois que l’expéditeur a la clé publique de son destinataire, il peut l’utiliser pour crypter les données qu’il souhaite sécuriser. Une fois qu’il a été chiffré avec une clé publique, il ne peut être déchiffré que par la clé privée de la même paire de clés. Même la même clé publique ne peut pas être utilisée pour déchiffrer les données. Cela est dû aux propriétés de fonctions de trappe que nous avons mentionné ci-dessus.

Lorsque le destinataire reçoit le message crypté, il utilise sa clé privée pour accéder aux données. Si le destinataire souhaite retourner les communications de manière sécurisée, ils peuvent ensuite crypter leur message avec la clé publique de la partie avec laquelle ils communiquent. Encore une fois, une fois qu’elles ont été chiffrées avec la clé publique, le seul moyen d’accéder aux informations est via la clé privée correspondante.

De cette façon, le cryptage RSA peut être utilisé par des parties jusque-là inconnues pour envoyer des données en toute sécurité entre elles. Des parties importantes des canaux de communication que nous utilisons dans notre vie en ligne ont été construites à partir de cette fondation.

Comment les messages plus compliqués sont-ils cryptés avec RSA?

Dans notre exemple, nous avons beaucoup simplifié les choses pour le rendre plus facile à comprendre, c’est pourquoi nous n’avons chiffré qu’un message de «4». Pouvoir chiffrer le chiffre 4 ne semble pas particulièrement utile, vous vous demandez peut-être comment chiffrer un ensemble de données plus compliqué, comme une clé symétrique (qui est l’utilisation la plus courante de RSA), ou même un message.

Certaines personnes peuvent être perplexes quant à la façon dont une clé comme «n38cb29fkbjh138g7fqijnf3kaj84f8b9f…» ou un message comme «achetez-moi un sandwich» peut être crypté par un algorithme comme RSA, qui traite des chiffres et non des lettres. La réalité est que toutes les informations que nos ordinateurs traitent sont stockées en binaire (1 et 0) et nous utilisons des normes de codage comme ASCII ou Unicode les représenter d’une manière que les humains peuvent comprendre (lettres).

Cela signifie que des clés comme «n38cb29fkbjh138g7fqijnf3kaj84f8b9f…» et des messages comme «achetez-moi un sandwich» existent déjà sous forme de nombres, qui peut être facilement calculé dans l’algorithme RSA. Les nombres qu’ils représentent sont beaucoup plus grands et plus difficiles à gérer, c’est pourquoi nous préférons traiter avec des caractères alphanumériques plutôt qu’avec un fouillis de binaires.

Si tu voulais crypter une clé de session plus longue ou un message plus complexe avec RSA, cela impliquerait simplement un nombre beaucoup plus important.

Rembourrage

Lorsque RSA est implémenté, il utilise quelque chose appelé rembourrage pour aider à prévenir un certain nombre d’attaques. Pour expliquer comment cela fonctionne, nous allons commencer par un exemple. Supposons que vous envoyiez un message codé à un ami:

Chère Karen,

    J’espère que vous allez bien. Sommes-nous toujours en train de dîner demain?

    Cordialement,

    James

Disons que vous avez codé le message de manière simple, en changer chaque lettre en celle qui la suit dans l’alphabet. Cela changerait le message en:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

Si vos ennemis ont intercepté cette lettre, il y a une astuce qu’ils pourraient utiliser pour essayer de casser le code. Ils pourraient regardez le format de votre lettre et essayez de deviner ce que le message pourrait dire. Ils savent que les gens commencent normalement leurs lettres par «Salut», «Bonjour», «Cher» ou un certain nombre d’autres conventions.

S’ils essayaient d’appliquer “Salut” ou “Bonjour” comme premier mot, ils verraient qu’il ne conviendrait pas au nombre de caractères. Ils pourraient alors essayer «Cher». Ça va, mais ça ne veut pas forcément dire quoi que ce soit. Les attaquants l’essayaient et voyaient où cela les menait. Ils changeraient donc les lettres «e», «f», «b» et «s» par «d», «e», «a» et «r» respectivement. Cela leur donnerait:

Cher Laseo,

    J ipqe zpv sont xemm. Are xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

Cela semble toujours assez déroutant, donc les attaquants pourraient essayer de regarder d’autres conventions, comme la façon dont nous concluons nos lettres. Les gens ajoutent souvent «De» ou «Cordialement» à la fin, mais ni l’un ni l’autre ne correspond au format. Au lieu de cela, les attaquants pourraient essayer «Cordialement» et remplacer les autres lettres pour voir où cela les mène. En changeant «z», «p», «v», «t», «j» «o», «d» et «m» par «y», «o», «u», «s», « i “,” n “,” c “et” l “respectivement, ils obtiendraient:

Cher Lasen,

    Je pense que vous êtes xell. Are xe tuill iawinh dinnes uonossox?

    Cordialement,

    Kanet

Après cette modification, il semble que les attaquants commencent à se rendre quelque part. Ils ont trouvé les mots «je», «vous» et «êtes», en plus des mots qui ont fait leurs suppositions initiales.

Étant donné que les mots sont dans l’ordre grammatical correct, les attaquants peuvent être assez confiants qu’ils vont dans la bonne direction. À ce jour, ils ont probablement également réalisé que le code impliquait que chaque lettre soit changée en celle qui la suit dans l’alphabet. Une fois qu’ils ont réalisé cela, il est facile de traduire le reste et de lire le message d’origine.

L’exemple ci-dessus n’était qu’un simple code, mais comme vous pouvez le voir, la structure d’un message peut donner aux attaquants des indices sur son contenu. Bien sûr, il était difficile de comprendre le message à partir de sa structure et il a fallu faire des suppositions éclairées, mais vous devez garder à l’esprit que les ordinateurs sont bien meilleurs pour ce faire que nous.. Cela signifie qu’ils peuvent être utilisés pour comprendre des codes beaucoup plus complexes en un temps beaucoup plus court, sur la base d’indices provenant de la structure et d’autres éléments.

Si la structure peut conduire à la fissuration d’un code et révéler le contenu d’un message, alors nous avons besoin d’un moyen de masquer la structure afin de sécuriser le message. Cela nous amène à rembourrage.

Lorsqu’un message est complété, des données randomisées sont ajoutées pour masquer les indices de mise en forme d’origine qui pourraient conduire à la rupture d’un message crypté. Avec RSA, les choses sont un peu plus compliquées, car une clé chiffrée n’a pas le formatage évident d’une lettre qui nous a aidés à nous donner des indices dans notre exemple ci-dessus.

Malgré cela, les adversaires peuvent utiliser un certain nombre d’attaques pour exploiter les propriétés mathématiques d’un code et casser des données chiffrées. En raison de cette menace, les implémentations de RSA utilisent des schémas de remplissage comme OAEP pour incorporer des données supplémentaires dans le message. L’ajout de ce remplissage avant le cryptage du message rend RSA beaucoup plus sûr.

Signature des messages

RSA peut être utilisé pour plus que le simple chiffrement de données. Ses propriétés en font également un système utile pour confirmant qu’un message a été envoyé par l’entité qui prétend l’avoir envoyé, et prouvant qu’un message n’a pas été altéré ou falsifié.

Lorsque quelqu’un veut prouver l’authenticité de son message, il peut calculer un hacher (une fonction qui prend des données d’une taille arbitraire et les transforme en valeur de longueur fixe) du texte en clair, puis signez-les avec leur clé privée. Ils signer le hachage en appliquant la même formule que celle utilisée pour le déchiffrement (m = cré mod n). Une fois le message signé, ils envoient cette signature numérique au destinataire à côté du message.

Si un destinataire reçoit un message avec une signature numérique, il peut utiliser le signature pour vérifier si le message a été authentifié par la clé privée de la personne qui prétend l’avoir envoyé. Ils peuvent également voir si le message a été modifié par les attaquants après son envoi.

Pour vérifier la signature numérique, le destinataire utilise d’abord la même fonction de hachage pour trouver la valeur de hachage du message qu’il a reçu. Le destinataire applique ensuite le clé publique de l’expéditeur à la signature numérique, en utilisant la formule de cryptage (c = me mod n), pour leur donner le hachage de la signature numérique.

Par comparer le hachage du message reçu avec le hachage de la signature numérique cryptée, le destinataire peut dire si le message est authentique. Si les deux valeurs sont identiques, le message n’a pas été modifié depuis sa signature par l’expéditeur d’origine. Si le message avait été modifié par un seul caractère, la valeur de hachage serait complètement différente.

Sécurité RSA & attaques

Comme la plupart des cryptosystèmes, la sécurité de RSA dépend de la façon dont il est implémenté et utilisé. Un facteur important est la taille de la clé. le plus le nombre de bits d’une clé est important (essentiellement la longueur de la clé), plus il est difficile de résoudre les attaques comme le forçage brutal et l’affacturage.

Étant donné que les algorithmes à clé asymétrique tels que RSA peuvent être brisés par factorisation d’entier, contrairement aux algorithmes à clé symétrique comme AES, les clés RSA doivent être beaucoup plus longues pour atteindre le même niveau de sécurité..

Actuellement, le la plus grande taille de clé prise en compte est de 768 bits. Cela a été fait par une équipe d’universitaires sur une période de deux ans, en utilisant des centaines de machines.

Étant donné que l’affacturage a été achevé fin 2009 et que la puissance de calcul a considérablement augmenté depuis lors, on peut supposer qu’une tentative d’intensité similaire pourrait désormais prendre en compte une clé RSA beaucoup plus grande.

Malgré cela, le temps et les ressources nécessaires à ce type d’attaque le mettent hors de portée de la plupart des pirates et dans le domaine des États-nations. La meilleure longueur de clé à utiliser dépendra de votre modèle de menace individuel. L’Institut national des normes et de la technologie recommande une taille de clé minimale de 2048 bits, mais des clés de 4096 bits sont également utilisées dans certaines situations où le niveau de menace est plus élevé.

L’affacturage n’est qu’un moyen de rompre le RSA. Un certain nombre d’autres attaques ont le potentiel de briser le cryptage avec une quantité de ressources plus faible, mais celles-ci dépendent de la mise en œuvre et d’autres facteurs, pas nécessairement RSA lui-même. Certains d’entre eux comprennent:

Les nombres premiers sont-ils vraiment aléatoires?

Certaines implémentations de RSA utilisent des générateurs de nombres aléatoires faibles pour trouver les nombres premiers. Si ces chiffres ne sont pas suffisamment aléatoires, il est beaucoup plus facile pour les attaquants de les prendre en compte et de casser le chiffrement. Ce problème peut être évité en utilisant un générateur de nombres pseudo-aléatoires cryptographiquement sécurisé.

Mauvaise génération de clés

Les clés RSA doivent correspondre à certains paramètres pour être sécurisées. Si les nombres premiers p et q sont trop proches les uns des autres, la clé peut être facilement découverte. De même, le nombre ré qui fait partie de la clé privée ne peut pas être trop petit. Une valeur faible facilite la résolution. Il est important que ces numéros soient d’une longueur suffisante pour garder votre clé en sécurité.

Attaques par canal latéral

Il s’agit d’un type d’attaque qui ne casse pas directement RSA, mais utilise plutôt les informations de son implémentation pour donner aux attaquants des conseils sur le processus de chiffrement. Ces attaques peuvent inclure des choses comme analyser la quantité d’énergie utilisée, ou analyse de prédiction de branche, qui utilise des mesures de temps d’exécution pour découvrir la clé privée.

Un autre type d’attaque latérale est connu sous le nom d’attaque temporelle. Si un attaquant a la possibilité de mesurer le temps de déchiffrement sur l’ordinateur de sa cible pour un certain nombre de messages chiffrés différents, ces informations peuvent permettre à l’attaquant de vérifier la clé privée de la cible.

La plupart des implémentations de RSA évitent cette attaque en ajoutant une valeur unique lors du processus de chiffrement, ce qui supprime cette corrélation. Ce processus est appelé aveuglement cryptographique.

Le chiffrement RSA est-il sûr pour l’avenir?

La bonne nouvelle est que RSA est considéré comme sûr à utiliser, malgré ces attaques possibles. La mise en garde est que il doit être implémenté correctement et utiliser une clé qui correspond aux paramètres corrects. Comme nous venons de le voir, les implémentations qui n’utilisent pas de remplissage, utilisent des nombres premiers de taille inadéquate ou présentent d’autres vulnérabilités ne peuvent pas être considérées comme sûres.

Si vous souhaitez utiliser le cryptage RSA, assurez-vous que vous utilisez une clé d’au moins 1024 bits. Ceux qui ont des modèles de menace plus élevés devraient s’en tenir à des clés de 2048 ou 4096 bits s’ils veulent utiliser RSA en toute confiance. Tant que vous êtes conscient des faiblesses de RSA et que vous l’utilisez correctement, vous devez vous sentir en sécurité pour utiliser RSA pour le partage de clés et d’autres tâches similaires qui nécessitent un cryptage à clé publique..

Voir également: Explication des types de chiffrement courants