Qu’est-ce que le chiffrement 3DES et comment fonctionne DES?

3DES est un chiffrement de chiffrement dérivé du Data Encryption Standard (DES) d’origine. Il est devenu important à la fin des années 90, mais est depuis tombé en disgrâce en raison de la montée d’algorithmes plus sécurisés.

Bien qu’il soit obsolète en 2023, il est toujours mis en œuvre dans certaines situations. Puisqu’il est basé sur l’un des premiers algorithmes largement publiés et étudiés, DES, il est toujours important de savoir ce qu’est 3DES et comment il fonctionne..

Ce guide vous guidera à travers chaque étape du processus DES en détail, puis expliquera comment le DES est modifié dans 3DES pour le rendre plus sécurisé. Il aborde également les différents problèmes de sécurité et indique si vous devez ou non utiliser l’algorithme.

Qu’est-ce que 3DES?

Bien qu’il soit officiellement connu sous le nom de Triple Data Encryption Algorithm (3DEA), il est généralement appelé 3DES. En effet, l’algorithme 3DES utilise le chiffrement Data Encryption Standard (DES) trois fois pour chiffrer ses données.

DES est un algorithme à clé symétrique basé sur un réseau Feistel. En tant que chiffrement à clé symétrique, il utilise la même clé pour les processus de chiffrement et de déchiffrement. Le réseau Feistel rend ces deux processus presque exactement les mêmes, ce qui se traduit par un algorithme plus efficace à mettre en œuvre.

DES a à la fois un bloc de 64 bits et une taille de clé, mais en pratique, la clé n’accorde que 56 bits de sécurité. 3DES a été développé comme une alternative plus sûre en raison de la petite longueur de clé de DES. Dans 3DES, l’algorithme DES est exécuté trois fois avec trois clés, mais il n’est considéré comme sécurisé que si trois clés distinctes sont utilisées.

Les utilisations de 3DES

Une fois que les faiblesses du DES normal sont devenues plus apparentes, 3DES a été adopté dans un large éventail d’applications. C’était l’un des schémas de cryptage les plus couramment utilisés avant la montée en puissance d’AES.

Quelques exemples de ses implémentations incluent les systèmes de paiement Microsoft Office, Firefox et EMV. Beaucoup de ces plateformes n’utilisent plus 3DES car il existe de meilleures alternatives.

L’Institut national des normes et de la technologie (NIST) a publié un projet de proposition indiquant que toutes les formes de 3DES seront obsolètes jusqu’en 2023 et interdites à partir de 2024. Bien qu’il ne s’agisse que d’un brouillon, la proposition signifie la fin d’une époque, et il est largement temps de passer à d’autres algorithmes plus sûrs.

L’histoire du chiffrement 3DES

Étant donné que 3DES est dérivé de DES, il est préférable d’introduire d’abord la norme antérieure. Dans les années 70, le National Bureau of Standards (NBS – il a depuis été renommé NIST) cherchait un algorithme qu’il pourrait utiliser comme norme pour crypter des informations gouvernementales sensibles mais non classifiées..

Le NBS a accepté des propositions pour une norme qui répondrait à ses exigences, mais aucun des candidats du tour initial n’était approprié. Il a invité plus de soumissions, et cette fois IBM a envoyé un algorithme que son équipe a développé. La soumission est dérivée du chiffre de Lucifer conçu par Horst Feistel.

En 1975, l’algorithme IBM a été publié par le NBS en tant que norme de chiffrement des données proposée. Le public a été invité à commenter le design, ce qui a suscité quelques critiques.

D’éminents cryptographes tels que Whitfield Diffie et Martin Hellman, concepteurs de l’échange de clés Diffie-Hellman, ont affirmé que la longueur de la clé était trop courte et que les boîtes S avaient été modifiées par rapport à leur conception initiale..

À l’époque, de nombreux membres de la communauté cryptographique pensaient que la NSA avait saboté le projet et affaibli l’algorithme, de sorte que ce serait la seule agence capable de casser DES.

Lorsque cela a été étudié par le Comité spécial du Sénat des États-Unis sur le renseignement, il a été constaté que la «NSA a convaincu IBM qu’une taille de clé réduite était suffisante; indirectement aidé au développement des structures S-box; et certifié que l’algorithme DES final était, au meilleur de leur connaissance, exempt de toute faiblesse statistique ou mathématique. »

Le même rapport a poursuivi en disant que la “NSA n’a pas altéré la conception en aucune façon.” Cela a été soutenu par certains anciens employés d’IBM qui ont affirmé que l’algorithme DES a été entièrement conçu par l’équipe IBM.

La propre documentation déclassifiée de la NSA affirme que l’agence «a travaillé en étroite collaboration avec IBM pour renforcer l’algorithme contre tout sauf les attaques par force brute et pour renforcer les tables de substitution…»

Les soupçons de falsification de la NSA ont été atténués dans les années 90 une fois que la cryptanalyse différentielle a été découverte publiquement. Lorsque les S-box tant décriées ont été testées avec la nouvelle technique, elles se sont révélées plus résistantes aux attaques que si elles avaient été choisies au hasard.

Cela indique que l’équipe IBM connaissait déjà la cryptanalyse différentielle dans les années 70, Steven Levy affirmant que la NSA leur avait demandé de garder la technique secrète afin de protéger la sécurité nationale..

Le célèbre cryptographe Bruce Schneier a un jour plaisanté: «Il a fallu deux décennies à la communauté universitaire pour comprendre que les« ajustements »de la NSA ont réellement amélioré la sécurité du DES.»

Malgré les questions initiales sur la sécurité de l’algorithme et l’implication de la NSA, l’algorithme IBM a ensuite été approuvé comme Data Encryption Standard en 1976. Il a été publié en 1977 et réaffirmé comme standard en 1983, 1988 et 1993.

Lorsque la cryptanalyse linéaire a été publiée pour la première fois en 1994, elle a commencé à soulever des questions sur la sécurité de l’algorithme. En 1997, le NIST a annoncé qu’il cherchait un algorithme pour remplacer DES. Le besoin d’un nouvel algorithme s’est intensifié à mesure que la technologie évoluait et que les attaques potentielles se renforçaient..

Diverses tentatives de craquage ont montré qu’il était moins difficile de casser l’algorithme qu’on ne le pensait auparavant. En 1998, distribué.net a pu cracker DES en 39 jours.

Début 1999, Deep Crack de l’Electronic Frontier Foundation avait réduit le temps à un peu plus de 22 heures. Cela signifiait la fin du DES, car une attaque de cette nature était désormais à la portée d’un adversaire bien doté..

Le problème principal était le petit espace clé, et un nouvel algorithme était absolument nécessaire. C’était un problème, car il faudrait encore plusieurs années au NIST pour s’installer sur l’algorithme qui est devenu le standard de remplacement, le Advanced Encryption Standard (AES).

Alors que le chiffre pour AES était en cours de décision, 3DES a été proposé comme mesure provisoire. Cela implique d’exécuter l’algorithme DES trois fois, avec trois clés distinctes. En 1999, DES a été réaffirmé, mais avec 3DES comme algorithme idéal. Le DES normal n’était autorisé que dans les applications héritées.

3DES est devenu un algorithme de cryptage répandu, bien que son utilisation intensive des ressources et les limitations de sécurité l’ont conduit à être remplacé par AES dans la majorité des cas d’utilisation.

Comprendre l’algorithme DES

Avant de parler des détails de 3DES, il est important de comprendre l’algorithme DES dont il est dérivé. Commençons donc dès le début.

Nous utilisons le chiffrement pour transformer nos données en clair en texte chiffré, qui sont des informations auxquelles les attaquants ne peuvent pas accéder (tant que nous utilisons des algorithmes appropriés).

Les algorithmes de chiffrement sont essentiellement des formules mathématiques complexes. Quand il s’agit de crypter quelque chose comme «Allons à la plage», beaucoup de gens sont confus. Après tout, comment pouvez-vous appliquer les mathématiques à des choses comme les lettres et les caractères?

Encodage du texte

La réalité est que les ordinateurs ne traitent pas les lettres et les caractères. Au lieu de cela, ils travaillent sur un système de 1 et de 0 appelé binaire. Chaque 1 ou 0 est connu comme un bit, et une collection de huit d’entre eux est connue comme un octet.

Vous pouvez soit le rechercher manuellement, soit utiliser un convertisseur en ligne pour voir qu’en binaire, «Allons à la plage» devient:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

Blocs

Lorsque les données sont cryptées, elles sont divisées en blocs distincts pour le traitement. DES a une taille de bloc de 64 bits, ce qui signifie essentiellement que chaque bloc correspond à un mélange de 64 uns et zéros. Notre premier bloc (les 64 premiers chiffres du binaire montré ci-dessus) serait:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Notre deuxième serait:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

Et notre dernier bloc serait:

01100010 01100101 01100001 01100011 01101000

Rembourrage

Vous avez peut-être remarqué que notre troisième bloc ne fait que 40 bits. Avant de pouvoir être chiffré, il doit être construit jusqu’à une taille de bloc 64 bits. Cela se fait avec rembourrage, ce qui implique d’ajouter des informations supplémentaires à un bloc afin de le compléter. Cela peut être fait avec un certain nombre de schémas différents, et cela peut également rendre les informations cryptées plus difficiles à déchiffrer, mais nous n’entrerons pas dans les détails dans cet article.

Le calendrier clé DES

Les algorithmes de chiffrement utilisent des clés pour ajouter des données qui modifieront le résultat final du processus. Si DES impliquait uniquement des étapes comme la permutation et les S-box (la permutation est expliquée ci-dessous, alors que les S-boxes sont couverts dans le Substitution section), tout ce qu’un attaquant aurait à faire serait de découvrir les détails de l’algorithme, puis de faire chacune des étapes à l’envers pour révéler le message initial.

Étant donné que la plupart de nos algorithmes sont largement connus, cela n’ajouterait pas vraiment beaucoup de sécurité. Au lieu de cela, des clés secrètes sont ajoutées pour modifier la sortie d’une manière qui ne peut pas être prédite simplement en connaissant l’algorithme (tant qu’un algorithme suffisamment complexe est utilisé).

DES commence par une seule clé, qui est utilisée pour créer des sous-clés qui sont appliquées à chaque tour. Il s’agit d’une clé 64 bits, de la même taille que nos blocs. Disons que notre clé est:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Maintenant, cette clé en binaire, qui est la façon dont les données sont exprimées lorsque les ordinateurs les traitent. Lorsque les humains manipulent des clés, elles apparaissent normalement sous la forme d’un mélange de caractères, quelque chose comme ceci:

kj329nf982bc9wn1

Dans DES, la première étape pour dériver nos clés rondes est de permuter la clé (la déplacer) selon le tableau suivant:

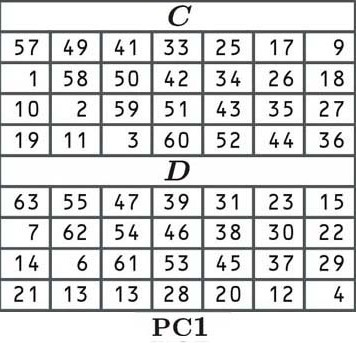
En permutation, chaque bit de notre clé d’origine est mélangé à une nouvelle position comme indiqué par le tableau. Étant donné que la cellule dans le coin supérieur gauche (de C) indique 57, le premier numéro de notre clé permutée sera le numéro en 57ème position de notre ancien bloc:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

La deuxième cellule dit 49, ce qui signifie que le deuxième chiffre de notre nouvelle clé sera le nombre qui est à la 49ème position de notre ancien bloc:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

La troisième cellule dit 41, nous recherchons donc le chiffre à la 41e position:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Jusqu’à présent, notre clé est composée de “110“.

Le reste de la clé est disposé de la même manière, selon les valeurs du tableau. Nous nous déplaçons de gauche à droite, et une fois que nous arrivons à la fin d’une rangée, nous sautons à la suivante, comme d’habitude. Une fois que tableau C est terminé, nous sautons à tableau D pour terminer la seconde moitié de la clé.

Il n’y a pas de moyen facile de transposer tout notre bloc selon la table de permutation initiale. Vous pouvez tout faire manuellement, ou écrire un script pour cela (ou même avoir de la chance et en trouver un dans les profondeurs d’Internet), mais nous allons tricher et inventer:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

Vous craignez peut-être que nous inventions certains des chiffres de ce guide, mais la réalité est que cela n’a pas vraiment d’importance. Plus personne ne crypte les données manuellement, tout se fait via des programmes. L’aspect le plus critique de ce tutoriel est que vous avez une idée claire des concepts que nous traitons. Les chiffres eux-mêmes ne servent qu’à vous aider à visualiser ce qui se passe.

Certains lecteurs ont peut-être remarqué que la table (et maintenant notre clé), n’a que 56 bits au lieu de 64. En effet, chaque huitième bit est ignoré. Il s’agit d’un artefact des anciens jours de la technologie, où il était important d’avoir des bits de contrôle de parité, qui vérifiaient si la clé avait été reçue correctement. Ces bits de contrôle de parité signifient qu’en pratique, DES n’a que la sécurité d’une clé de 56 bits.

Les tableaux C et D nous donnent une clé qui a deux moitiés de 28 bits. Parfois, les moitiés sont appelées C et D, mais tout au long de cet article, nous les désignerons comme L et R, pour gauche et droite. Notre côté gauche est:

1100010 1010010 1010101 0101010

Bien que notre droit soit:

1010000 1111001 0001011 1000111

L’étape suivante consiste à décaler la clé d’un ou deux espaces vers la gauche, selon le tour. Le nombre exact d’espaces est décidé selon le tableau prédéterminé suivant:

Nombre de tours Nombre de décalages à gauche

1	1
2	1
3	2
4	2
5	2
6	2
sept	2
8	2
9	1
dix	2
11	2
12	2
13	2
14	2
15	2
16	1

Prenons donc nos moitiés gauche et droite:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

Et déplacez-les tous les deux d’une position vers la gauche, car le premier tour a un décalage de 1 selon le tableau (le numéro à gauche est déplacé à droite).

Sous-clé du premier tour:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

Au deuxième tour, le tableau indique également 1, donc ce résultat sera à nouveau modifié en déplaçant chaque position numéro un vers la gauche.

Deuxième tour sous-clé:

L 1001010 1001010 1010101 01010dix

R 1000011 1100100 0101110 00111dix

Au troisième tour, les numéros seront déplacés de deux places vers la gauche, car le tableau indique maintenant 2.

Sous-clé du troisième tour:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

Lors des tours suivants, les nombres sont déplacés vers la gauche en fonction des distances spécifiées dans le tableau, chaque décalage étant appliqué au résultat du tour précédent. En fin de compte, cela nous donne seize sous-clés différentes, une pour chaque cycle du processus DES.

L’étape suivante est une autre permutation selon le tableau PC2 ci-dessous:

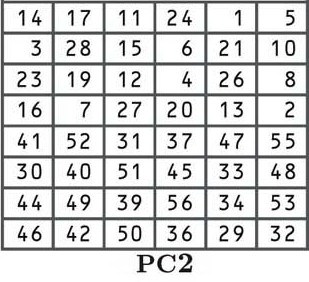
À ce stade, vous devez être familier avec les permutations, donc nous n’entrerons pas dans le processus en profondeur. Si vous souhaitez voir comment cela fonctionne plus en détail, reportez-vous à l’explication au début de cette section. Bien que les postes de réinstallation soient différents, le processus est le même.

Chacune des 16 touches dérivées du processus de décalage est maintenant mélangée selon le tableau, avec le numéro de la 14e position déplacé à la première place, la 17e à la seconde, la 11e à la troisième, etc…

Si vous regardez attentivement le tableau, vous remarquerez qu’il n’y a que 48 bits, plutôt que les 56 bits que nous avions auparavant. Ce processus est connu sous le nom de permutation de compression.

Vous pouvez également voir que la moitié supérieure du tableau comporte des nombres entre un et 28, tandis que la moitié inférieure contient des nombres de 29 à 56. Cela maintient les moitiés gauche et droite de nos sous-clés séparées, et il est indiqué ci-dessous par le plus grand espace au milieu des touches.

Encore une fois, nous allons tricher et inventer les chiffres. Disons que tout ce processus nous a donné les sous-clés suivantes:

Premier tour:         010101 010101 101010 110100 101001 100101 101010 101010

Deuxième round:         011010 110101 101110 110010 010100 110010 111101 101101

Troisième tour:     010100 100110 110110 101010 100110 011000 101011 011001

Quatrième tour:         011001 110101 011001 110101 000011 001011 010101 010101

Cinquième manche:         110101 001101 010101 010101 010011 001011 010111 100101

Sixième round:           010111 110101 011001 111001 101001 100101 101010 101010

Septième manche:     110101 111010 101110 101010 100110 010110 111011 001110

Huitième tour:       011001 110101 010101 001001 010011 001011 010100 101010

Round neuf:         111011 011010 011110 100010 100010 010110 110011 110010

Tour 10:             011010 010101 101110 101001 010010 010110 111000 101010

Round 11:             110101 001101 101110 101010 100101 100101 101010 001010

Tour 12:             101001 100100 101001 101010 100110 011000 101011 011001

Tour 13:             010010 010010 010101 010101 010110 110001 100101 101010

Tour 14:             101001 100110 010101 011101 010001 001010 110010 111110

Tour 15:             011001 011010 011001 110101 001001 011001 100101 101101

Tour 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Ce processus de décalage entraîne l’utilisation de chaque bit de la clé initiale dans environ 14 des 16 sous-clés, bien que certains bits soient légèrement plus utilisés que d’autres..

Permutation initiale

Une fois les données divisées en blocs et complétées si nécessaire, il est temps de commencer le processus de cryptage DES. Nous reviendrons sur les sous-clés que nous venons de créer à un stade ultérieur. La première étape est connue sous le nom de permutation initiale, où les données sont réorganisées selon le tableau suivant:

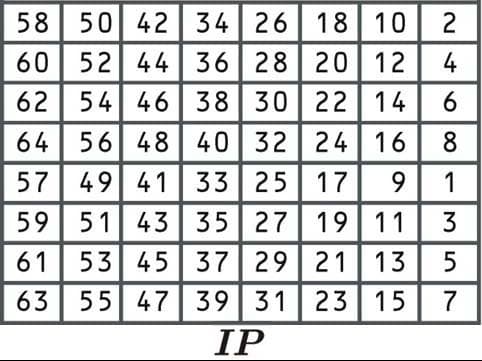
Ce processus de permutation initial ne rend pas l’algorithme plus sûr. En effet, cela n’implique la saisie d’aucune touche et peut facilement être inversé. L’algorithme a été initialement conçu de cette façon car il a facilité l’implémentation dans certains contextes.

Étant donné que nous avons couvert les permutations plusieurs fois, nous allons ignorer toute explication majeure ici. Retournez à Le calendrier clé DES section si vous avez besoin de plus d’informations sur leur fonctionnement.

Prenons le premier bloc du message «Allons à la plage», que nous avons dérivé dans le Bloquer section sous Comprendre l’algorithme DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Depuis la première cellule dit 58, nous sélectionnerions le nombre de la 58e position:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Ensuite, nous prendrions le nombre de la 50e position:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Et le nombre de la 42e position:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Cela nous donne «110” jusque là. Nous composerons le reste du nombre:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Lorsque la permutation initiale est terminée, les données sont passées à l’étape suivante.

Fractionner les blocs

Une fois que les données ont subi leur permutation initiale, elles sont divisées en deux moitiés. On prend notre bloc qui vient de subir sa permutation initiale:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Et nous allons le séparer en deux blocs, un bloc de gauche (composé des 32 premiers chiffres), appelé L0:

L0    11010111 01001010 10101000 10011101

Et un bloc de droite (composé des 32 seconds chiffres), appelé R0:

R0    01001011 10110101 10000111 10101001

La fonction F

Maintenant que le bloc a été divisé, il est temps que la fonction F ait lieu. Au premier tour, il ne sera appliqué que sur la moitié droite du bloc, tandis que la moitié gauche sera mise de côté jusqu’à plus tard. Le côté droit subit les quatre étapes suivantes dans le cadre de la fonction F:

• Permutation d’expansion (E dans le diagramme)
• Mélange de touches (⊕ dans le diagramme)
• Substitution (chaque S1, S2 etc. dans le diagramme)
• Permutation (P dans le diagramme)

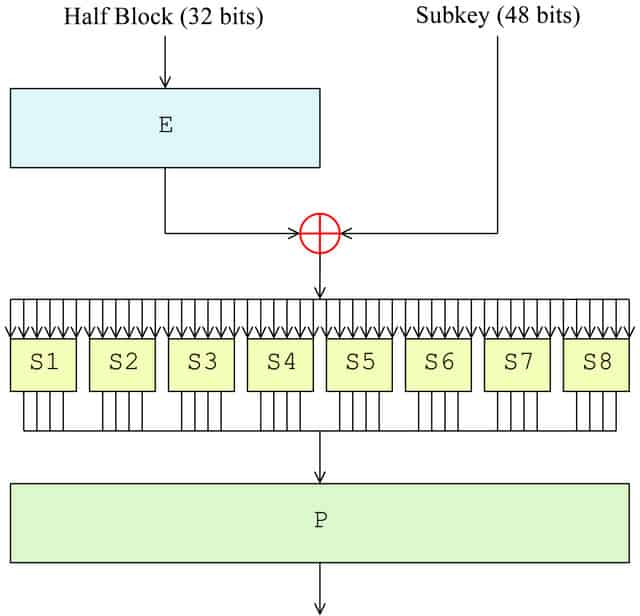
Permutation d’expansion

La permutation d’expansion accomplit trois choses. Le plus important est qu’il permet à des bits de données d’entrée uniques d’affecter la sortie de deux autres bits, provoquant un effet d’avalanche. Il fait également la moitié droite de 48 bits, de sorte qu’il ait la même taille que la sous-clé pour l’étape suivante. L’autre effet de la permutation d’expansion est qu’elle rend la sortie plus longue que l’entrée. Cela lui permet d’être compressé dans l’opération de substitution.

Les bits sont réorganisés conformément au tableau suivant. Certains des bits individuels sont dans le tableau deux fois, c’est ainsi que le bloc est passé de 32 à 48 bits:

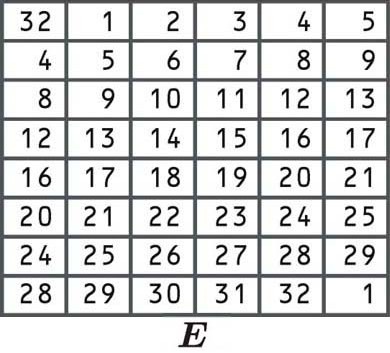
Puisque la première cellule indique 32, nous prenons notre bloc de droite et sélectionnons le nombre à partir de la 32e position, tout comme nous l’avons fait dans les autres exemples de permutation répertoriés ci-dessus:

R0    01001011 10110101 10000111 10101001

Nous prenons ensuite les chiffres de la première position, de la deuxième position et ainsi de suite, jusqu’à ce que nous arrivions dans le coin inférieur droit du bloc. Puisqu’il y a 1 dans cette cellule, le dernier chiffre sera également le nombre qui apparaît en première position de notre bloc.

Disons que la permutation d’expansion nous donne un nouveau bloc de 48 bits de:

101110 100110 100100 000000 001100 001110 101101 011110

Mélange de touches

Une fois que le bloc a été étendu à 48 bits, il est temps d’appliquer la sous-clé du premier tour, que nous avons dérivée dans le Calendrier clé DES section ci-dessus. Le bloc est modifié par la sous-clé à l’aide du chiffrement XOR.

Le chiffrement XOR est un chiffrement d’addition qui suit un processus simple, surtout par rapport aux autres éléments dont nous avons déjà discuté.

Dans un chiffrement XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Disons que vous devez XOR les deux nombres suivants en binaire:

1101

0101

Chaque chiffre serait ajouté à celui en dessous. Selon les trois règles ci-dessus, cela donne un résultat de:

1000

Pour terminer l’étape de mélange des clés, nous prenons le côté droit de notre bloc que nous venons d’étendre à 48 bits, et la première clé ronde. Nous effectuons ensuite l’ajout XOR:

Bloquer:                      101110 100110 100100 000000 001100 001110 101101 011110

Première clé:     010101 010101 101010 110100 101001 100101 101010 101010

Résultat XOR:             111011 110011 001110 110100 100101 101011 000111 110100

Le résultat de l’opération XOR est ensuite transmis au tour suivant.

Substitution

La substitution ajoute de la confusion aux données. Cela se fait normalement avec des tables de recherche, également appelées boîtes de substitution ou S-box. DES utilise huit tables ou S-box distinctes, une différente pour chaque 6 bits de données. Le tableau suivant présente les huit boîtes S du DES:

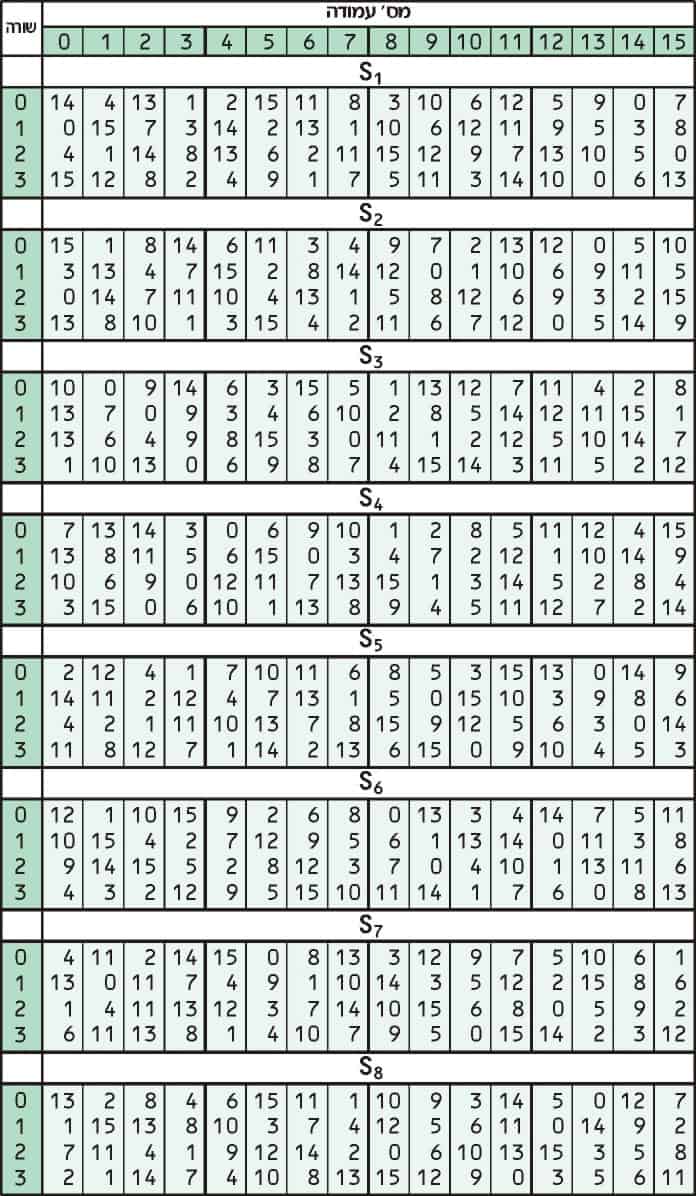
Les huit boîtiers S séparés sont utilisés pour traduire chaque entrée 6 bits en une sortie 4 bits. La première étape du processus consiste à prendre les chiffres au début et à la fin d’un segment de 6 bits, puis à convertir cette valeur binaire en décimal.

Prenons les données que nous venons de terminer XORing à l’étape précédente:

111011 110011 001110 110100 100101 101011 000111 110100

Nous allons examiner le premier segment 6 bits pour vous montrer comment fonctionne le processus de substitution:

111011

Puisque le premier nombre et le dernier nombre sont tous les deux 1, cela nous donne une valeur de 11. Nous convertissons ensuite 11 du binaire au décimal, ce qui nous donne 3. Ce ne sont que des valeurs équivalentes, écrites de différentes manières. Considérez-le comme une conversion du langage informatique en langage humain. Vous pouvez vérifier la conversion par vous-même avec une calculatrice en ligne si vous le souhaitez.

Nous prenons ensuite les quatre chiffres du milieu du premier segment de 6 bits:

111011

Et les convertir du binaire en décimal. 1101 se traduit par le numéro 13.

Maintenant, nous prenons ces deux nombres et les recherchons dans le S1 table:

               

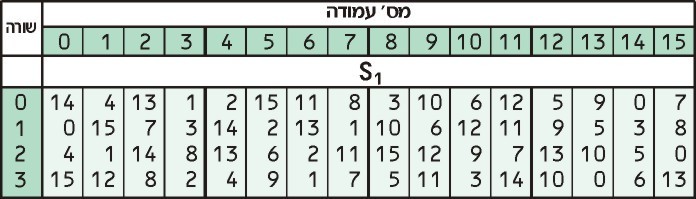
Notre premier numéro, 3, nous dit de regarder dans la troisième rangée, tandis que notre deuxième numéro, 13 nous dit de regarder dans la 13e colonne. La valeur de la troisième ligne de la 13e colonne est 0.

Maintenant que nous avons recherché notre nombre dans le tableau, nous le reconvertissons en binaire à quatre chiffres. Zéro est normalement écrit comme 0 en binaire, mais 0000 est le même, et c’est le format qui convient le mieux à nos besoins.

À la suite de ce processus, la S-box convertit notre première section de données 6 bits (111011) dans une valeur 4 bits différente (0000). Cela semble compliqué, mais cette technique aide à obscurcir davantage la relation entre le texte chiffré et le texte en clair auquel il est lié..

La section de données suivante de 6 bits passe ensuite par le même processus, mais à la place, elle utilise la case S2 illustrée ci-dessus. La troisième section utilise la table S3 et ainsi de suite, jusqu’à ce que la section finale subisse la substitution via la table S8.

Encore une fois, nous allons tricher pour le reste des valeurs. Disons que les cases de substitution nous donnent un résultat de:

0000 1010 1100 1001 0100 1001 0111 0001

Une fois que chaque section des données a traversé sa S-box, elle passe à l’étape suivante.

Permutation

La dernière étape de la fonction F est une autre permutation, en utilisant le tableau suivant: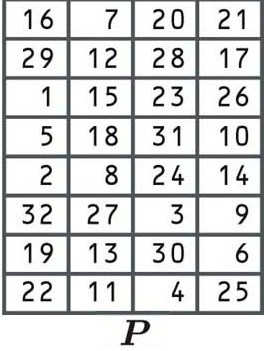

À présent, vous devriez avoir une bonne compréhension de la façon dont les permutations déplacent les chiffres de l’ancien bloc vers une position différente dans le nouveau bloc, donc nous n’y reviendrons pas.

Disons que cette permutation prend notre résultat précédent:

0000 1010 1100 1001 0100 1001 0111 0001

Et nous donne une sortie de:

0101 0110 1001 0101 0010 0100 0101 0010

Maintenant que la permutation est terminée, nous avons terminé avec les quatre étapes de la fonction F dans ce tour. En notation mathématique, cette valeur est appelée f (R0, K1). Cela signifie que le résultat est la fonction (F) du côté droit initial du bloc (R0) et de la sous-clé du premier tour (K1).

XOR avec le bloc gauche

Rappelez-vous comment nous avons divisé le bloc en deux juste avant de commencer les étapes de la fonction F? Nous avons mis de côté le côté gauche du bloc (L0), tandis que le côté droit a subi chacun de ces processus. Eh bien, il est maintenant temps pour L0 de revenir à l’action.

Nous prenons le bon côté que nous venons de traiter f (R0, K1) et l’ajouter à l’ancien côté gauche (L0) à l’aide du chiffrement XOR. Cela nous donne R1, le résultat de notre premier tour:

f (R0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0:                                    1101 0111 0100 1010 1010 1000 1001 1101

Résultat XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Se référer au Mélange de touches section ci-dessus si vous avez besoin d’un rappel du fonctionnement du chiffrement XOR.

15 tours de plus…

Si vous êtes allé aussi loin, alors DES semble probablement être un processus ardu. Mais ce n’est même pas encore près d’être terminé. Les données passent par les quatre étapes de la fonction F, suivies du XOR, encore 15 fois, pour un total de 16 tours.

Au deuxième tour, nous prenons la version originale et intacte du côté droit du bloc (R0) et en faisons le nouveau côté gauche (L1). Pendant ce temps, nous prenons le résultat de notre premier tour et l’envoyons via la fonction F. Tout se passe de la même manière que la dernière fois, mais cette fois, la sous-clé du deuxième tour est utilisée à la place. Disons que ce processus nous donne un résultat de:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Nous avons ensuite XOR le résultat avec L1, qui est en fait R0 (nous avons dérivé cela dans le Blocs de fendage section). Cela nous donne le résultat du deuxième tour, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Cette étape peut sembler un peu déroutante, mais sous le schéma Feistel, l’ancien côté droit devient le nouveau côté gauche, tandis que le résultat de l’opération devient le nouveau côté droit.

Le diagramme suivant vous donne une représentation visuelle de ce qui se passe. IP représente la permutation initiale, F est un remplaçant pour toute la fonction F, le ⊕ symbolise la fonction XOR et les flèches indiquent chaque côté du bloc se déplaçant entre la gauche et la droite:

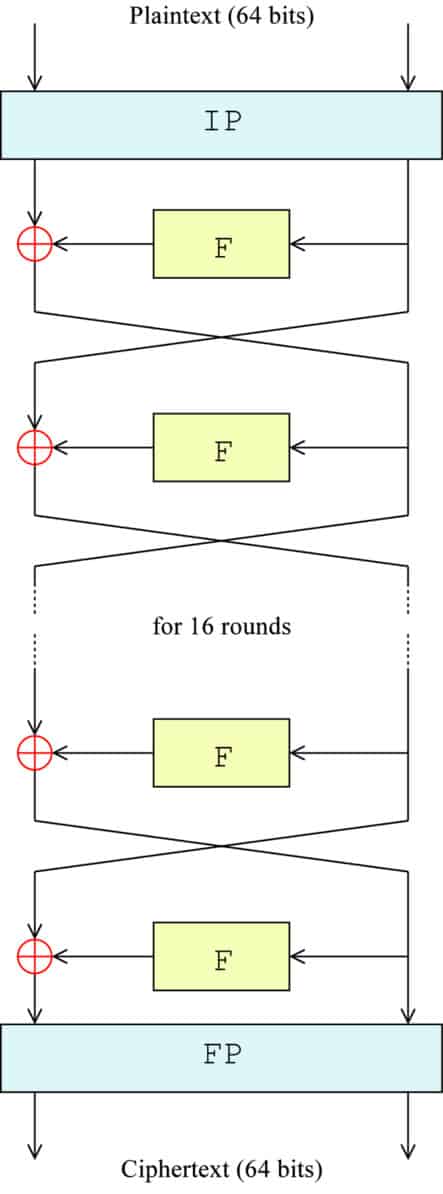
La formule exacte pour chaque étape est:

Ln = Rn-1

Rn = Ln-1 + F(Rn-1,Kn)

Où:

L = La moitié gauche du bloc (commençant par L0 lorsque le bloc a été initialement divisé)

R = La moitié droite du bloc (commençant par R0 lorsque le bloc a été initialement divisé)

n = le numéro du tour (commençant par 0, lorsque le bloc a été initialement divisé)

f = La fonction F

Kn = la sous-clé du tour n

Selon la formule et le diagramme, au troisième tour, R1 devient la nouvelle moitié gauche (L2), tandis que R2 est traité par la fonction F. Disons que cela nous donne un résultat de:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Nous calculons ensuite le résultat de notre troisième tour (R3), en utilisant le chiffrement XOR, comme précédemment:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

Le même processus se poursuit jusqu’au quinzième tour, les blocs basculant et la sous-clé suivante étant utilisée à chaque tour. Au 16e et dernier tour, les blocs ne sont pas inversés. Au lieu de cela, ils sont combinés pour former un bloc 64 bits. S’abstenir d’échanger les blocs dans cette dernière étape permet à l’algorithme d’être utilisé à la fois pour le chiffrement et le déchiffrement.

Disons que le tour final nous donne un résultat de:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Permutation finale

Cette permutation est l’inverse de la permutation initiale, et là encore, elle n’ajoute aucune valeur de sécurité supplémentaire. Il réorganise les données selon le tableau suivant:

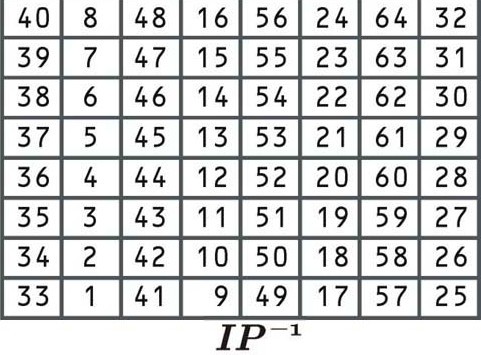
Cette table de permutation fonctionne de la même manière que les précédentes. Comme il s’agit de la dernière étape du processus de cryptage, le résultat sera le texte chiffré du premier bloc de “Allons-y à la plage”. Disons que le bloc chiffré est:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Maintenant, si vous vouliez le vrai texte chiffré pour «Allons à la plage», vous auriez pu sauter tout le processus d’apprentissage et passer directement à un outil de chiffrement DES en ligne. Si nous entrons notre phrase à côté d’une clé (disons kj329nf982bc9wn1), l’outil nous donne un texte chiffré de:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Si vous le souhaitez, vous pouvez ensuite convertir la clé et le texte chiffré en binaire, puis comparer comment texte chiffré du premier bloc s’aligne avec l’ensemble du processus qui a été décrit.

Décryptage DES

Dans DES, le processus de décryptage est incroyablement simple. La structure Feistel de l’algorithme permet de l’inverser facilement. Le processus est exécuté presque exactement de la même manière pour décrypter les informations. La seule différence est que les sous-clés sont appliquées en sens inverse. Il s’agit d’une configuration efficace, car cela signifie que les mêmes logiciels et matériels peuvent être utilisés à la fois dans les processus de chiffrement et de déchiffrement..

Pour décrypter les données, il passe d’abord par une permutation initiale, puis le bloc est divisé et la moitié droite passe par la fonction F. La différence est que lors du premier cycle de décryptage, la 16e sous-clé est appliquée. Tout le reste se déroule normalement. Une fois la fonction F terminée, elle est XOR avec le côté gauche du bloc.

Les blocs sont inversés et le résultat passe par le même processus pour le deuxième tour, à la seule exception que la 15e sous-clé est appliquée. Ce processus se poursuit jusqu’au 16e tour, lorsque la 1ère sous-clé est utilisée.

Tout comme dans le processus de cryptage, les blocs ne sont pas échangés au stade final, puis les données subissent une permutation finale. Ceci termine le processus de décryptage, résultant en le texte en clair d’origine du message.

3DES

Comme les faiblesses de sécurité de DES sont devenues plus apparentes, 3DES a été proposé comme un moyen d’étendre sa taille de clé sans avoir à construire un algorithme entièrement nouveau. Plutôt que d’utiliser une seule clé comme dans DES, 3DES exécute l’algorithme DES trois fois, avec trois clés de 56 bits:

• La clé est utilisée pour Crypter le texte en clair.
• La clé deux est utilisée pour décrypter le texte qui avait été chiffré par la clé un.
• La troisième clé est utilisée pour Crypter le texte déchiffré par la clé trois.

À chaque étape, le processus DES complet est suivi comme indiqué ci-dessus.

Maintenant, vous vous demandez peut-être “Comment l’application du décryptage dans la deuxième étape peut-elle améliorer la sécurité?”

La réponse est qu’elle utilise une clé distincte. Si la première clé était également utilisée pour déchiffrer les données dans la deuxième étape, les données seraient de retour là où elles ont commencé.

Cependant, comme il utilise une clé différente, le processus de décryptage ne sert pas réellement à décrypter les données. Cela peut sembler logiquement pervers, mais le déchiffrement avec une clé distincte ne sert qu’à embrouiller encore plus les données.

Une fois que la deuxième clé a «déchiffré» les données, la troisième clé est appliquée pour les crypter à nouveau. Le résultat est le texte chiffré 3DES.

3DES est structuré de cette façon car il permet aux implémentations d’être compatibles avec le DES à clé unique, le DES à deux clés et le DES à trois clés (ceux-ci sont traités dans la section suivante). Cela ne fonctionnerait pas si le cryptage était utilisé dans les trois étapes.

Options de saisie 3DES

Techniquement, 3DES peut être implémenté avec trois configurations de clés différentes. Malgré cela, les deuxième et troisième options sont précaires et ne devraient jamais être mises en œuvre.

• Première option de saisie – Cette option utilise trois clés indépendantes et est la plus sécurisée.
• Option de saisie deux – Dans cette configuration, les première et troisième touches sont les mêmes.
• Option de saisie trois – Cela utilise trois clés identiques. Lorsque des clés identiques sont utilisées, le processus de décryptage dans la deuxième étape annule le premier cryptage, ne laissant que le cryptage final pour modifier les données. Cela fait du résultat identique au DES ordinaire.

Le processus 3DES: Keying option one

Soyons honnêtes, l’intégralité du processus 3DES peut vous faire tourner la tête, surtout si vous êtes nouveau dans la cryptographie. Pour l’aider à pénétrer, voici un bref résumé de l’ensemble du schéma de cryptage de l’algorithme 3DES:

Le texte en clair entre dans l’algorithme 3DES et est d’abord chiffré avec une clé dans les étapes suivantes:

• • Calendrier des clés – les 16 sous-clés sont dérivées de la clé 1

  • Permutation initiale

  • Le bloc est divisé en moitiés gauche et droite

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé du tour

      • Substitution

      • Permutation

    • XOR le résultat de la fonction F avec le côté gauche

    • Faire de l’ancien côté droit le nouveau côté gauche, et le résultat du nouveau côté droit

      Répétez les étapes ci-dessus 14 fois

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé pour le 16e tour

      • Substitution

      • Permutation

    • XOR le résultat de la fonction F avec le côté gauche

    • Combinez les côtés gauche et droit du bloc ensemble

• • Permutation finale

Prenez le texte qui a été chiffré avec la première clé, puis envoyez-le via le Processus de «décryptage» avec clé deux:

• • Calendrier des clés – les 16 sous-clés sont dérivées de la clé deux

  • Permutation initiale

  • Le bloc est divisé en moitiés gauche et droite

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé pour le tour (à partir de la 16ème sous-clé pour le déchiffrement)

      • Substitution

      • Permutation

    • XOR le résultat de la fonction F avec le côté gauche

    • Faire de l’ancien côté droit le nouveau côté gauche et le résultat du nouveau côté droit

      Répétez les étapes ci-dessus 14 fois

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé pour le premier tour

      • Substitution

      • Permutation

    • XOR le résultat de la fonction F avec le côté gauche

    • Combinez les côtés gauche et droit du bloc ensemble
  • Permutation finale

Prenez les données qui ont été «déchiffrées» par la clé deux, puis envoyez-les via le enprocessus de cryption avec clé Trois:

• • Calendrier clé – les 16 sous-clés sont dérivées de la clé trois

  • Permutation initiale

  • Le bloc est divisé en moitiés gauche et droite

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé du tour

      • Substitution

      • Permutation

    • XOR le résultat de la fonction F avec le côté gauche

    • Faire de l’ancien côté droit le nouveau côté gauche, et le résultat du nouveau côté droit

      Répétez les étapes ci-dessus 14 fois

• • • La moitié droite est envoyée via la fonction F

      • Permutation d’expansion

      • XOR avec la sous-clé pour le 16e tour

      • Substitution

      • Permutation

    • OU le résultat de la fonction F avec le côté gauche

    • Combinez les côtés gauche et droit du bloc ensemble

• • Permutation finale

Le résultat est le texte chiffré 3DES.

La sécurité de 3DES

La sécurité de 3DES dépend de l’option de saisie utilisée. L’option de clé 1 implique trois clés 56 bits différentes, ce qui lui donne une longueur totale de clé de 168 bits. La longueur effective est considérablement réduite par les attaques de type rencontre, ce qui réduit sa sécurité dans le monde réel à 112 bits.

Les attaques Meet-in-the-middle sont utiles contre les schémas de chiffrement qui répètent plusieurs fois le même algorithme. La technique stocke les valeurs immédiates de chaque étape de chiffrement, puis utilise ces informations pour améliorer radicalement le temps qu’il faudrait pour forcer brutalement l’algorithme.

Les options deux et trois ont des clés beaucoup plus petites et sont vulnérables aux attaques de texte en clair connu et choisi, ainsi que d’autres.

Les attaques connues en clair sont possibles lorsqu’un adversaire a accès à la fois au texte en clair et au texte chiffré d’un message. Si un algorithme est sensible à ces attaques, l’attaquant peut utiliser ces informations pour déduire la clé, ce qui lui permet de casser toutes les autres données qui ont été chiffrées par la même clé.

Une attaque de texte en clair choisi est similaire, mais elle implique que l’attaquant découvre la clé en comparant des textes chiffrés à des textes en clair arbitraires.

En raison de ces vulnérabilités et des petites tailles de clés globales impliquées, les options de clé deux et trois ne sont pas sécurisées et ne doivent pas être mises en œuvre.

3DES est-il sûr?

Étant donné que 3DES sera obsolète au cours des prochaines années, il est préférable d’utiliser d’autres algorithmes. Bien que l’option de clé 1 soit toujours considérée comme sécurisée pour de nombreuses applications, il n’y a pas de bonnes raisons pour lesquelles elle devrait être utilisée à la place d’une alternative comme AES.

Bien que 3DES occupe une place importante dans la cryptographie en tant que suivi de DES, ses années de gloire sont terminées et il est temps de passer à autre chose. Si vous souhaitez sécuriser vos systèmes dans le futur, vous devriez plutôt utiliser un algorithme plus à jour.

En relation: Explication des types de chiffrement courants

Plan X par le DoD sous licence CC0