ما هو تشفير RSA وكيف يعمل؟

تشفير RSA هو نظام يعمل على حل ما كان من أكبر المشاكل في التشفير: كيف يمكنك إرسال رسالة مشفرة لشخص ما دون وجود فرصة لمشاركة الكود مسبقًا معهم?

هذه المادة سوف يعلمك كل ما تحتاج لمعرفته كيف تم تطوير تشفير RSA, كيف تعمل, الرياضيات وراء ذلك, ما يستخدم ل وكذلك بعض من أكبر القضايا الأمنية التي تواجهها. سيمنحك التعرف على RSA بعض المعرفة الأساسية التي تساعدك على فهم عدد أجزاء حياتنا على الإنترنت التي يتم الحفاظ عليها آمنة.

ما هو تشفير RSA?

دعنا نقول أنك تريد أن تخبر صديقك سرا. إذا كنت بجوارهم مباشرةً ، فيمكنك فقط همسه. إذا كنت على طرفي نقيض من البلد ، فمن الواضح أن هذا لن ينجح. يمكنك تدوينها وإرسالها بالبريد الإلكتروني لهم ، أو استخدام الهاتف ، ولكن كل من قنوات الاتصال هذه غير آمنة وأي شخص لديه دافع قوي بما فيه الكفاية يمكنه اعتراض الرسالة بسهولة.

إذا كان السر مهمًا بما فيه الكفاية ، فلن تخاطر بكتابته بشكل طبيعي – فقد يتفقد جواسيس أو موظف بريد مارق عبر بريدك. وبالمثل ، يمكن لأي شخص التنصت على هاتفك دون علمك وتسجيل كل مكالمة واحدة تقوم بها.

حل واحد لمنع المتنصتات من الوصول إلى محتويات الرسالة هو تشفيرها. هذا يعني في الأساس إضافة رمز إلى الرسالة التي تحوله إلى فوضى مختلطة. إذا كانت الكود الخاص بك معقدًا بما فيه الكفاية ، فسيكون الأشخاص الوحيدون الذين يمكنهم الوصول إلى الرسالة الأصلية هم الأشخاص الوحيدون الذين يمكنهم الوصول إلى الرسالة الأصلية.

إذا كانت لديك فرصة لمشاركة الكود مع صديقك مسبقًا ، إذن يمكن لأي منكم إرسال رسالة مشفرة في أي وقت, مع العلم أنكما هما الوحيدان اللذان لديهما القدرة على قراءة محتويات الرسالة. ولكن ماذا لو لم تكن لديك فرصة لمشاركة الكود مسبقًا?

هذه هي واحدة من المشاكل الأساسية للتشفير ، والتي تم معالجتها من قبل أنظمة تشفير المفتاح العام (المعروفة أيضًا باسم التشفير غير المتماثل) مثل RSA.

تحت تشفير RSA ، يتم تشفير الرسائل برمز يسمى a المفتاح العمومي, والتي يمكن مشاركتها علنا. بسبب بعض الخصائص الرياضية المميزة لخوارزمية RSA, بمجرد تشفير الرسالة باستخدام المفتاح العمومي ، لا يمكن فك تشفيرها إلا بواسطة مفتاح آخر ، يعرف باسم المفتاح الخاص. لكل مستخدم RSA زوج مفاتيح يتكون من مفاتيحه العامة والخاصة. كما يوحي الاسم ، يجب أن يبقى المفتاح الخاص سريًا.

تختلف مخططات تشفير المفتاح العام عن تشفير المفتاح المتماثل ، حيث تستخدم كل من عملية التشفير وفك التشفير نفس المفتاح الخاص. تجعل هذه الاختلافات تشفير المفتاح العمومي مثل RSA مفيدًا للتواصل في الحالات التي لا توجد فيها فرصة لتوزيع المفاتيح مسبقًا بأمان.

خوارزميات المفتاح المتناظر لها تطبيقات خاصة بها ، مثل تشفير البيانات للاستخدام الشخصي ، أو عندما يكون هناك قنوات آمنة يمكن مشاركة المفاتيح الخاصة عبرها.

أنظر أيضا: تشفير المفتاح العام

أين يتم استخدام تشفير RSA?

غالبًا ما يستخدم تشفير RSA في جنبا إلى جنب مع مخططات التشفير الأخرى, أو ل التوقيعات الرقمية والتي يمكن أن تثبت صحة ونزاهة الرسالة. لا يتم استخدامه عمومًا لتشفير الرسائل أو الملفات بأكملها ، لأنها أقل كفاءة وأثقل الموارد من تشفير المفتاح المتماثل.

لجعل الأمور أكثر كفاءة, سيتم تشفير الملف عمومًا باستخدام خوارزمية مفتاح متماثل ، ثم تشفير المفتاح المتماثل باستخدام تشفير RSA. بموجب هذه العملية ، لن يتمكن من فك تشفير المفتاح المتماثل سوى الكيان الذي لديه حق الوصول إلى المفتاح RSA الخاص.

دون أن تكون قادرة على الوصول إلى مفتاح متماثل ، و لا يمكن فك تشفير الملف الأصلي. يمكن استخدام هذه الطريقة للحفاظ على الرسائل والملفات آمنة ، دون أن تستغرق وقتًا طويلاً أو تستهلك الكثير من الموارد الحسابية.

يمكن استخدام تشفير RSA في عدد من الأنظمة المختلفة. يمكن تنفيذه في OpenSSL و wolfCrypt و cryptlib وعدد من مكتبات التشفير الأخرى.

كواحد من أول برامج تشفير المفتاح العام المستخدمة على نطاق واسع ، وضعت RSA الأسس لكثير من اتصالاتنا الآمنة. كانت تستخدم تقليديا في TLS وكان أيضا الخوارزمية الأصلية المستخدمة في تشفير PGP. لا يزال يتم مشاهدة RSA في مجموعة من متصفحات الويب والبريد الإلكتروني وشبكات VPN والدردشة وقنوات الاتصال الأخرى.

غالبًا ما يستخدم RSA لإجراء اتصالات آمنة بين عملاء VPN وخوادم VPN. بموجب بروتوكولات مثل OpenVPN ، يمكن لمصادقة TLS استخدام خوارزمية RSA لتبادل المفاتيح وإنشاء قناة آمنة.

خلفية تشفير RSA

كما ذكرنا في بداية هذه المقالة ، وقبل تشفير المفتاح العام ، كان من الصعب التواصل بشكل آمن إذا لم تكن هناك فرصة لتبادل المفاتيح بأمان مسبقًا. إذا لم تكن هناك فرصة لمشاركة الكود في وقت مبكر ، أو قناة آمنة يمكن من خلالها توزيع المفاتيح ، فلن تكون هناك طريقة للاتصال دون تهديد أعداء قادرين على اعتراض محتويات الرسالة والوصول إليها.

لم يكن حتى السبعينات من القرن الماضي بدأت الأمور تتغير بالفعل. تم نشر أول تطور رئيسي نحو ما نسميه الآن تشفير المفتاح العام في بداية العقد من قبل James H. Ellis. لم يتمكن إليس من إيجاد طريقة لتنفيذ عمله ، ولكن تم توسيعه بواسطة زميله كليفورد كوكس ليصبح ما نعرفه الآن باسم تشفير RSA.

الجزء الأخير من اللغز هو ما نسميه الآن ديفي هيلمان تبادل المفاتيح. اكتشف مالكولم ج. ويليامسون ، وهو زميل آخر في العمل ، خطة سمحت للطرفين بمشاركة مفتاح تشفير ، حتى إذا تمت مراقبة القناة بواسطة الخصوم.

تم تنفيذ كل هذا العمل في وكالة الاستخبارات البريطانية ، مقر الاتصالات الحكومية (GCHQ) ، والتي أبقى اكتشاف سرية. نظرًا جزئيًا للقيود التكنولوجية ، لم يتمكن GCHQ من رؤية استخدام تشفير المفتاح العام في ذلك الوقت ، لذلك ظل التطوير مكتوفي الأيدي على الغبار الذي يجمع الأرفف. لم يتم رفع السرية عن العمل حتى عام 1997 وتم الاعتراف بالمخترعين الأصليين من RSA.

بعد عدة سنوات ، بدأت مفاهيم مماثلة في التطور في المجال العام. رالف ميركل خلق شكل مبكر من تشفير المفتاح العام, التي أثرت على ويتفيلد ديفي ومارتن هيلمان في تصميم تبادل مفتاح ديفي هيلمان.

كانت أفكار ديفي وهيلمان تفتقد أحد الجوانب المهمة التي من شأنها أن تجعل عملهم أساسًا لتشفير المفاتيح العامة. كان هذا وظيفة أحادية الاتجاه من الصعب قلبها. في عام 1977, رون ريفست ، عدي شامير وليونارد أدلمان, أسماؤهم الأخيرة تشكل اختصارًا RSA ، تم التوصل إلى حل بعد عام من العمل على حل المشكلة.

حقق الأكاديميون في معهد ماساتشوستس للتكنولوجيا انطلاقة بعد حفلة عيد الفصح في عام 1977. بعد ليلة من الشرب ، عاد ريفست إلى المنزل ، ولكن بدلاً من النوم ، أمضى المساء محمومًا في كتابة ورقة أضفت عليها فكرته عن الوظيفة الرسمية في اتجاه واحد..

لقد حصلت MIT على براءة الاختراع في عام 1983 ، لكن خوارزمية RSA لم تبدأ إلا في الأيام الأولى لشبكة الإنترنت في رؤية التبني على نطاق واسع كأداة أمنية مهمة.

كيف يعمل تشفير RSA?

سيكون ما يلي تبسيطًا قليلاً ، لأن الكثير من القراء ربما تعرضوا للندب من قبل مدرس الرياضيات في المدرسة الثانوية. للحفاظ على الرياضيات من الخروج عن السيطرة ، سنكون كذلك تبسيط بعض المفاهيم واستخدام أرقام أصغر بكثير. في الواقع ، يستخدم تشفير RSA أعدادًا أولية أكبر من حيث الحجم وهناك عدد قليل من التعقيدات الأخرى.

هناك العديد من المفاهيم المختلفة التي سيتعين عليك لفت انتباهها قبل أن نتمكن من شرح مدى ملاءمتها. وتشمل هذه وظائف trapdoor وتوليد الأعداد الأولية ووظيفة Carmichael الكاملة والعمليات المنفصلة التي تشارك فيها حساب المفاتيح العامة والخاصة المستخدمة في عمليات التشفير وفك التشفير.

وظائف الباب فخ

يعمل تشفير RSA وفقًا لفرضية أن الخوارزمية هي من السهل حسابها في اتجاه واحد ، ولكن يكاد يكون من المستحيل في الاتجاه المعاكس. على سبيل المثال ، إذا تم إخبارك أن 701،111 هو نتاج رقمين أوليين ، هل ستكون قادرًا على معرفة ماهية هذين الرقمين?

حتى مع وجود آلة حاسبة أو كمبيوتر ، لن يكون لدى معظمنا أي فكرة عن المكان الذي يجب أن نبدأ به ، ناهيك عن أن نكون قادرين على معرفة الإجابة. لكن إذا قلبنا الأمور ، فسيصبح الأمر أسهل بكثير. ما هي نتيجة:

907 × 773

إذا كنت تشعر بالملل الكافي ، فستتمكن من ضرب هاتفك أو ربما حسابه في رأسك لاكتشاف أن الإجابة هي 701111 المذكورة سابقًا. يمثل هذان الرقمان 907 و 773 الأعداد الأولية التي تجيب على سؤالنا الأول ، والذي يوضح لنا أن بعض المعادلات قد يكون من السهل تحديد طريقة واحدة ، ولكن يبدو أنها مستحيلة في الاتجاه المعاكس.

جانب آخر مثير للاهتمام في هذه المعادلة هو أنه من السهل معرفة أحد الأرقام الأولية إذا كان لديك بالفعل الرقم الآخر ، وكذلك المنتج. إذا تم إخبارك أن 701،111 هو نتيجة 907 مضروبة في عدد أولي آخر ، فيمكنك استنتاج رقم أولي آخر باستخدام المعادلة التالية:

701111 ÷ 907 = 773

نظرًا لأن العلاقة بين هذه الأرقام بسيطة لحسابها في اتجاه واحد ، ولكن في الاتجاه المعاكس بشكل لا يصدق ، تُعرف المعادلة باسم وظيفة الباب فخ. كن على دراية بأنه على الرغم من أن المثال أعلاه يصعب على الأشخاص اكتشافه ، إلا أن أجهزة الكمبيوتر يمكنها القيام بالعملية في فترة تافهة من الوقت.

لهذا السبب ، يستخدم RSA أعداد أكبر بكثير. يختلف حجم الأعداد الأولية في تطبيق RSA الحقيقي ، ولكن في 2048 بت RSA ، سيجتمعون لإنشاء مفاتيح يبلغ طولها 617 رقمًا. لمساعدتك في تصور ذلك ، سيكون المفتاح هو عدد من هذا الحجم:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

توليد الأعداد الأولية

تشكل وظائف باب الملاءمة المذكورة أعلاه الأساس لكيفية عمل أنظمة تشفير المفتاح العام والخاص. تسمح خصائصها بمشاركة المفاتيح العامة دون تعريض الرسالة للخطر أو الكشف عن المفتاح الخاص. كما أنها تسمح بتشفير البيانات باستخدام مفتاح واحد بطريقة لا يمكن فك تشفيرها إلا بواسطة المفتاح الآخر من الزوج.

الخطوة الأولى لتشفير رسالة باستخدام RSA هي توليد المفاتيح. للقيام بذلك ، نحن بحاجة رقمين رئيسيين (ص و ف) التي يتم اختيارها مع اختبار البدائية. اختبار البدائية هو خوارزمية تجد الأعداد الأولية بكفاءة ، مثل اختبار بدائية Rabin-Miller.

يجب أن تكون الأعداد الأولية في RSA كبيرة جدًا ، وأن تكون متباعدة نسبيًا. الأرقام الصغيرة أو الأوثق مع بعضها أسهل بكثير. على الرغم من ذلك ، سيستخدم مثالنا أرقامًا أصغر لتسهيل متابعة الأمور وحسابها.

دعنا نقول أن اختبار البدائية يعطينا الأعداد الأولية التي استخدمناها أعلاه ، 907 و 773. والخطوة التالية هي اكتشاف المعامل (ن) ، باستخدام الصيغة التالية:

ن = ص س ف

أين ص = 907 و ف = 773

وبالتالي:

ن = 907 × 773

ن = 701111

وظيفة كارمايكل الكاملة

بمجرد أن لدينا ن, نحن نستخدم وظيفة كارمايكل الكاملة:

    λ(ن) = لكم] (ص – 1, ف – 1)

إذا مرت بعض الوقت منذ أن وصلت إلى كتب الرياضيات ، فقد يبدو ما سبق مرعباً بعض الشيء. يمكنك تخطي هذا الجزء وتثق فقط في أن الرياضيات تعمل ، وإلا يمكنك التمسك ببعض الحسابات الإضافية. سيتم شرح كل شيء بأكبر قدر ممكن من التفاصيل لمساعدتك في جذب انتباهك حول الأساسيات.

بالنسبة لأولئك الذين ليسوا على علم, λ (ن) يمثل مجمل كارمايكل لـ ن, في حين لكم] يعني المضاعف المشترك الأدنى, وهو أقل عدد على حد سواء ص و ف يمكن أن تنقسم إلى. هناك بعض الطرق المختلفة لاكتشاف ذلك ، ولكن الأسهل هو الثقة في آلة حاسبة على الإنترنت للقيام بالمعادلة من أجلك. لذلك دعونا نضع أرقامنا في المعادلة:

    λ(701111) = لكم] (907 – 1, 773 – 1)

    λ(701111) = لكم] (906, 772)

   باستخدام الآلة الحاسبة المرتبطة أعلاه ، هذا يعطينا:

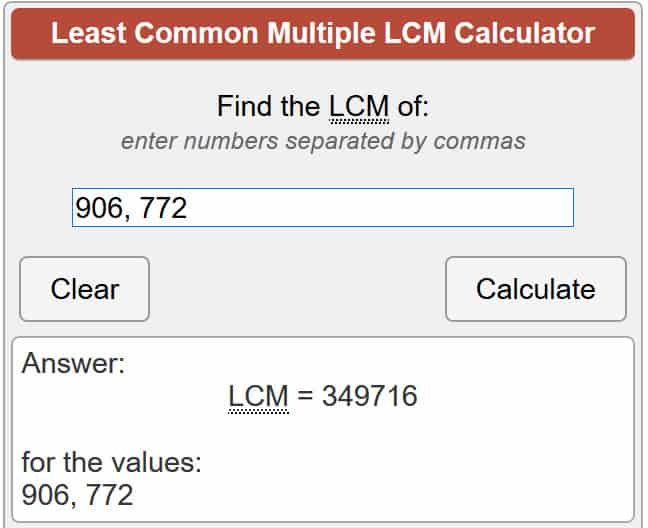
    λ(701111) = 349،716

توليد المفتاح العمومي

والآن بعد أن أصبح لدينا عدد كارمايكل الكامل لأعدادنا الأولية ، فإن الأمر كذلك الوقت لمعرفة مفتاحنا العام. تحت RSA, تتكون المفاتيح العامة من عدد أولي البريد, طالما ن. الرقم البريد يمكن أن يكون أي شيء بين 1 وقيمة λ(ن) ، وهو في مثالنا 3491616.

نظرًا لأن المفتاح العمومي مشترك بشكل مفتوح ، فهذا ليس مهمًا جدًا البريد ليكون رقم عشوائي. في التمرين, البريد يتم تعيين عموما في 65537, لأنه عندما يتم اختيار أعداد أكبر بكثير بشكل عشوائي ، فإنه يجعل التشفير أقل كفاءة بكثير. على سبيل المثال اليوم ، سنبقي الأرقام صغيرة لإجراء عمليات حسابية فعالة. دعنا نقول:

البريد = 11

تسمى بياناتنا المشفرة النهائية بالنص المشفر (ج). نشتقها من رسالة النص العادي لدينا (م) ، عن طريق تطبيق المفتاح العمومي بالصيغة التالية:

ج = مالبريد وزارة الدفاع ن

لقد توصلنا بالفعل مع البريد ونحن نعرف ن كذلك. الشيء الوحيد الذي نحتاج إلى شرحه هو عصري. إنه بعيد قليلاً عن عمق هذه المقالة ، لكنه يشير إلى أ عملية modulo, وهذا يعني بشكل أساسي الباقي المتبقي عندما تقسم جانبًا على الآخر. فمثلا:

10 عصري 3 = 1

وذلك لأن 3 يذهب إلى 10 ثلاث مرات ، مع ما تبقى من 1.

العودة إلى المعادلة لدينا. لإبقاء الأمور بسيطة ، دعنا نقول ذلك الرسالة (م) أننا نريد تشفير والحفاظ على السر هو مجرد رقم واحد, 4. دعنا ندخل كل شيء في:

ج = مالبريد عصري ن

ج = 411 عصري 701111

ج = 4،194304 عصري 701111

مرة أخرى ، لجعل عملية modulo من السهل ، سوف نستخدم آلة حاسبة على الإنترنت ، ولكن نرحب بك لمعرفة ذلك بنفسك. عن طريق إدخال 4،194،304 في الحاسبة عبر الإنترنت ، فإنه يعطينا:

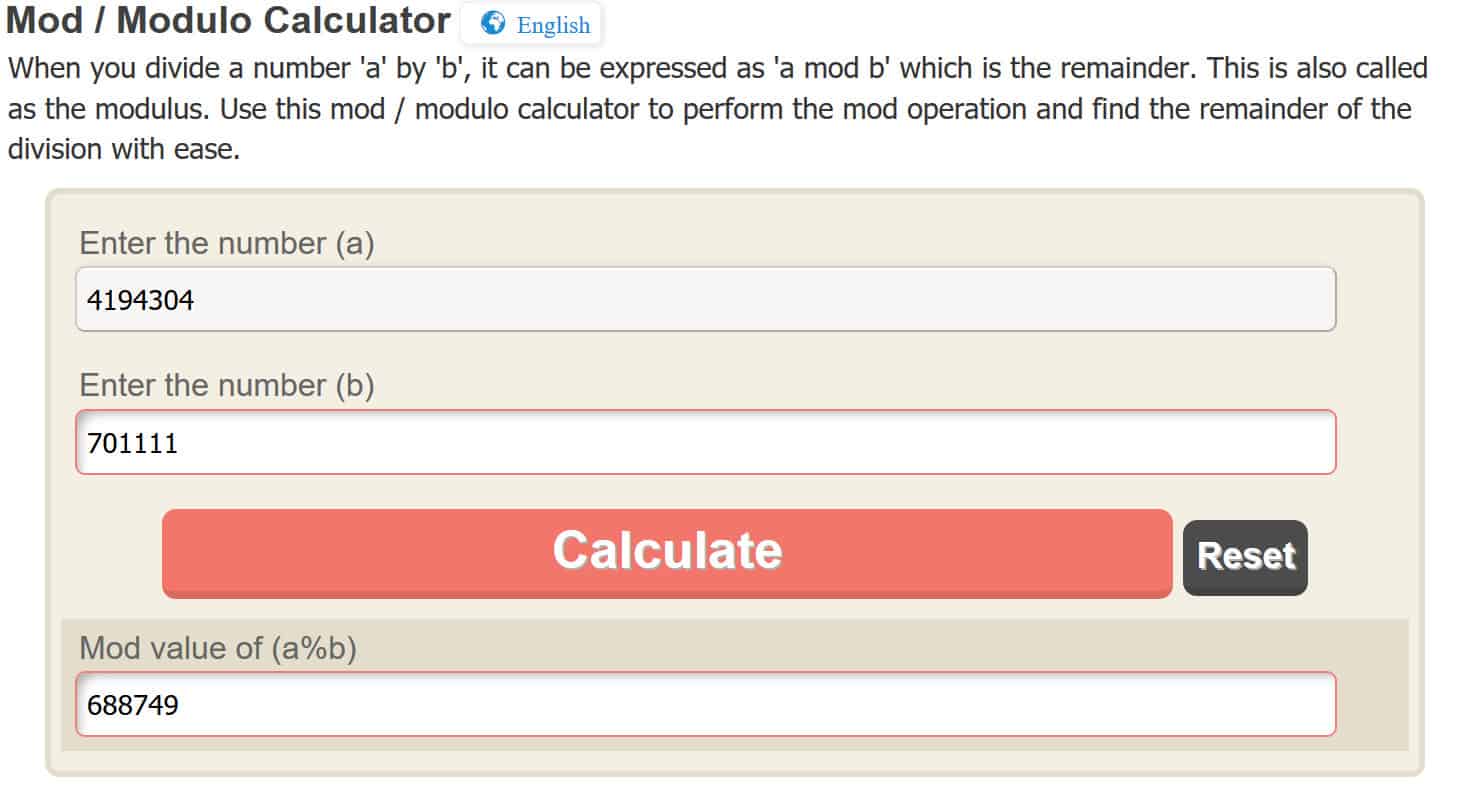
ج = 68849

لذلك عندما نستخدم RSA لتشفير رسالتنا, 4, مع المفتاح العام لدينا ، فإنه يعطينا النص المشفر 68849. قد تبدو الخطوات السابقة ثقيلة بعض الشيء في الرياضيات ، ولكن من المهم تكرار ما حدث بالفعل.

كان لدينا رسالة من 4, الذي أردنا أن نحافظ عليه سرا. قمنا بتطبيق مفتاح عمومي عليه ، مما أعطانا نتيجة مشفرة من 68849. الآن بعد أن تم تشفيرها, يمكننا أن نرسل بشكل آمن الرقم 688.749 إلى صاحب زوج المفاتيح. هم الشخص الوحيد الذي سيتمكن من فك تشفيره باستخدام المفتاح الخاص. عندما يقومون بفك تشفيرها ، سيرون الرسالة التي كنا نرسلها بالفعل, 4.

توليد المفتاح الخاص

في تشفير RSA ، بمجرد تحويل البيانات أو الرسالة إلى نص مشفر باستخدام مفتاح عمومي ، يمكن فك تشفيره فقط بواسطة المفتاح الخاص من نفس زوج المفاتيح. تتكون المفاتيح الخاصة من د و ن. ونحن نعلم بالفعل ن, والمعادلة التالية تستخدم لإيجاد د:

د = 1 /البريد وزارة الدفاع λ(ن)

في ال توليد المفتاح العمومي القسم أعلاه ، قررنا بالفعل في مثالنا, البريد سوف يساوي 11. وبالمثل ، نحن نعرف ذلك λ(ن) يساوي 3491616 من عملنا السابق تحت وظيفة كارمايكل الكاملة. تصبح الأمور أكثر تعقيدًا عندما نواجه هذا القسم من الصيغة:

1 /البريد عصري

قد تبدو هذه المعادلة أنها تطلب منك قسمة 1 على 11 ، لكن هذا ليس هو الحال. بدلا من ذلك ، هذا يرمز فقط أننا بحاجة إلى حساب معكوس وحدات من البريد (وهو في هذه الحالة 11) و λ(ن) (وهو في هذه الحالة 3491616).

هذا يعني أساسا أن بدلاً من إجراء عملية قياسية ، سنستخدم معكوس بدلاً من ذلك. يوجد هذا عادةً مع خوارزمية Extended Euclidean Algorithm ، ولكنه خارج نطاق هذه المقالة قليلاً ، لذلك سنقوم فقط بالغش واستخدام آلة حاسبة عبر الإنترنت بدلاً من ذلك. الآن وقد فهمنا كل ما يجري ، فلنربط معلوماتنا بالصيغة:

د = 1 /11 عصري 349716

لتنفيذ هذه العملية ، ببساطة أدخل 11 (أو أي قيمة قد تكون ل البريد إذا كنت تحاول هذا مع المثال الخاص بك) حيث تقول عدد صحيح و 349،716 (أو أي قيمة قد تكون ل λ(ن) إذا كنت تحاول هذا مع مثال خاص بك) حيث تقول مودولو في الحاسبة عبر الإنترنت التي تم ربطها أعلاه. إذا كنت قد فعلت ذلك بشكل صحيح ، يجب أن تحصل على نتيجة حيث:

د = 254 ، 339

الآن أن لدينا قيمة ل د, يمكننا فك تشفير الرسائل التي تم تشفيرها باستخدام مفتاحنا العام باستخدام الصيغة التالية:

م = جد وزارة الدفاع ن

يمكننا الآن العودة إلى النص المشفر الذي قمنا بتشفيره تحت توليد المفتاح الخاص الجزء. عندما قمنا بتشفير الرسالة باستخدام المفتاح العمومي ، أعطانا قيمة ج من 68849. من فوق ، نحن نعرف ذلك د يساوي 254،339. نحن نعلم ذلك أيضًا ن يساوي 701111. هذا يعطينا:

م = 68849254339 عصري 701111.

كما قد تلاحظ ، قد تكون محاولة أخذ رقم إلى القوة 254،339 أكثر قليلاً بالنسبة لمعظم الآلات الحاسبة العادية. بدلاً من ذلك ، سوف نستخدم حاسبة فك تشفير RSA عبر الإنترنت. إذا كنت ترغب في استخدام طريقة أخرى ، فستطبق الصلاحيات كما تفعل عادة وتنفذ عملية المعامل بالطريقة نفسها التي اتبعناها في توليد المفتاح العمومي الجزء.

في الحاسبة المرتبطة أعلاه ، أدخل 701111 حيث تقول معامل العرض: ن, 254،399 حيث تقول مفتاح فك التشفير: د, و 688.749 حيث تقول نص مشفر رسالة في شكل رقمي, كما هو مبين أدناه:

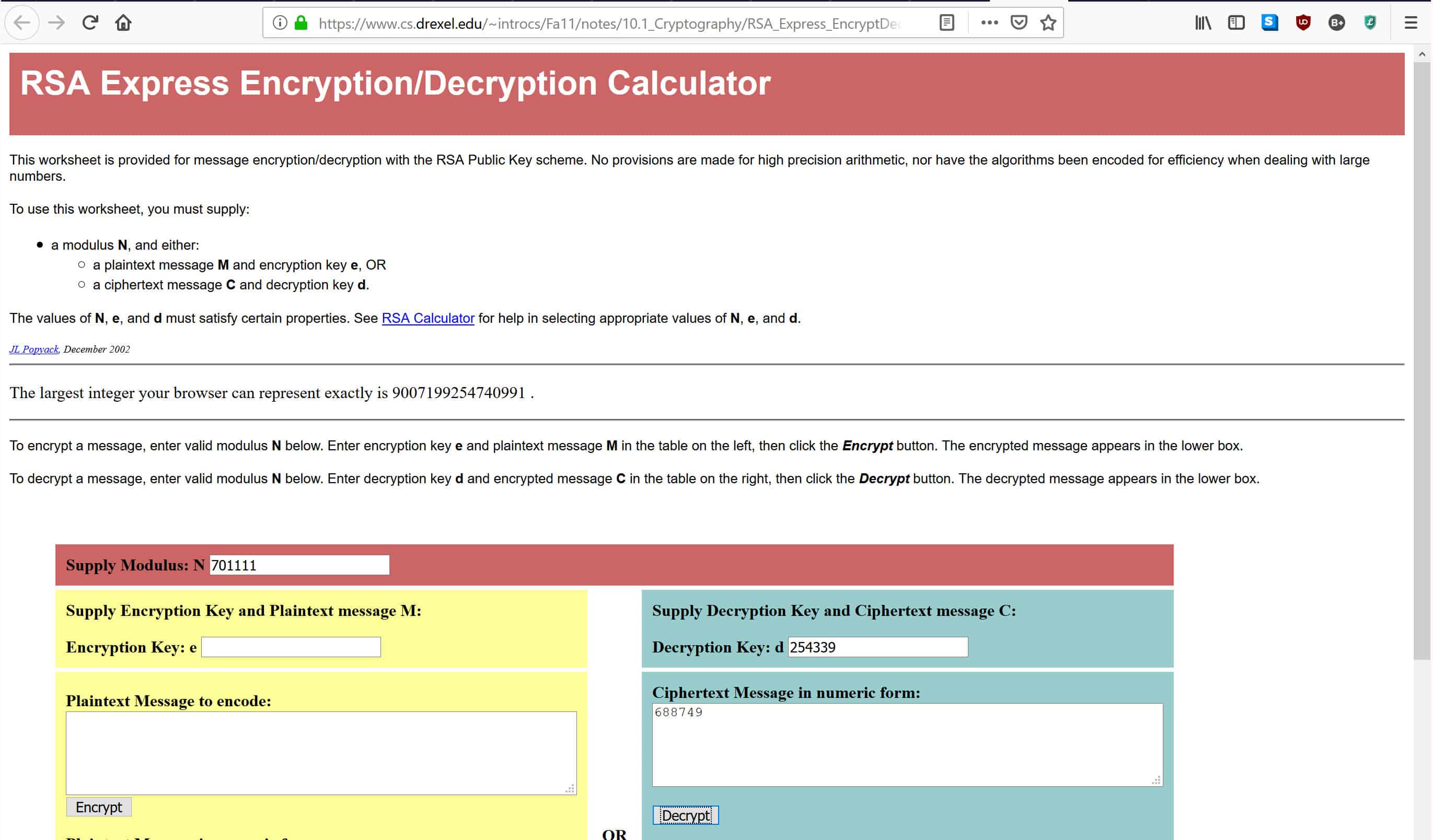
بمجرد إدخال البيانات ، اضغط على فك, والتي سوف تضع الأرقام من خلال صيغة فك التشفير التي تم سردها أعلاه. هذا سيعطيك الرسالة الأصلية في المربع أدناه. إذا كنت قد فعلت كل شيء بشكل صحيح ، يجب أن تحصل على إجابة 4, التي كانت الرسالة الأصلية التي قمنا بتشفيرها باستخدام المفتاح العمومي الخاص بنا.

كيف يعمل تشفير RSA في الممارسة العملية

يجب أن تمنحك الأقسام المذكورة أعلاه فهمًا معقولًا لكيفية عمل الرياضيات وراء تشفير المفتاح العام. قد يكون الأمر مربكًا بعض الشيء ، لكن حتى أولئك الذين لم يفهموا تعقيدات المعادلات يمكنهم أن يأخذوا بعض المعلومات المهمة عن العملية.

في الخطوات المذكورة أعلاه ، أظهرنا كيف يمكن لكيانين التواصل بشكل آمن دون مشاركة الرمز مسبقًا مسبقًا. أولاً ، يحتاج كل منهم إلى اقامة أزواجهم الرئيسية الخاصة و مشاركة المفتاح العام مع بعضها البعض. يحتاج الكيانان إلى الحفاظ على سرية المفاتيح الخاصة بهما حتى تظل اتصالاتهما آمنة.

بمجرد أن يكون لدى المرسل المفتاح العمومي للمستلم ، يمكنه استخدامه لتشفير البيانات التي يريدون الحفاظ عليها آمنة. بمجرد أن يتم تشفيره باستخدام مفتاح عام ، لا يمكن فك تشفيره إلا بواسطة المفتاح الخاص من نفس زوج المفاتيح. حتى المفتاح العمومي نفسه لا يمكن استخدامه لفك تشفير البيانات. هذا بسبب خصائص وظائف الباب فخ التي ذكرناها أعلاه.

عندما يتلقى المستلم الرسالة المشفرة ، يستخدمون المفتاح الخاص للوصول إلى البيانات. إذا أراد المستلم إرجاع الاتصالات بطريقة آمنة, يمكنهم بعد ذلك تشفير رسالتهم بالمفتاح العام للحزب الذي يتواصلون معه. مرة أخرى ، بمجرد أن يتم تشفيرها باستخدام المفتاح العمومي ، فإن الطريقة الوحيدة للوصول إلى المعلومات هي من خلال المفتاح الخاص المطابق.

وبهذه الطريقة ، يمكن استخدام تشفير RSA بواسطة أطراف غير معروفة مسبقًا لإرسال البيانات بشكل آمن فيما بينهم. تم بناء أجزاء كبيرة من قنوات الاتصال التي نستخدمها في حياتنا عبر الإنترنت من هذه المؤسسة.

كيف يتم تشفير الرسائل الأكثر تعقيدًا باستخدام RSA?

في مثالنا ، قمنا بتبسيط الأشياء كثيرًا لتسهيل فهمها ، ولهذا السبب قمنا بتشفير رسالة “4” فقط. لا يبدو أن القدرة على تشفير الرقم 4 مفيدة بشكل خاص ، لذلك قد تتساءل كيف يمكنك تشفير مجموعة أكثر تعقيدًا من البيانات, مثل مفتاح متماثل (وهو الاستخدام الأكثر شيوعًا لـ RSA) ، أو حتى رسالة.

قد يشعر بعض الناس بالحيرة من كيفية تشفير مفتاح مثل “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” أو رسالة مثل “buy me a sandwich” بواسطة خوارزمية مثل RSA ، والتي تتعامل مع الأرقام وليس الحروف. الحقيقة هي أن جميع المعلومات التي تعالجها أجهزة الكمبيوتر لدينا يتم تخزينها في ثنائي (1s و 0s) ونحن نستخدم معايير الترميز مثل أسكي أو يونيكود لتمثيلهم بطرق يمكن للبشر فهمها (رسائل).

هذا يعني ذاك مفاتيح مثل “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” ورسائل مثل “buy me a sandwich” موجودة بالفعل كأرقام, والتي يمكن حسابها بسهولة في خوارزمية RSA. الأرقام التي يمثلونها أكبر بكثير وأصعب بالنسبة لنا لإدارة ، وهذا هو السبب في أننا نفضل التعامل مع الأحرف الأبجدية الرقمية بدلاً من الخليط الثنائي.

أذا كنت ترغب ب قم بتشفير مفتاح جلسة أطول أو رسالة أكثر تعقيدًا مع RSA ، فستتضمن ببساطة عددًا أكبر بكثير.

حشوة

عندما يتم تطبيق RSA ، فإنه يستخدم ما يسمى الحشو للمساعدة في منع عدد من الهجمات. لشرح كيف يعمل هذا ، سنبدأ بمثال. دعنا نقول أنك كنت ترسل رسالة مشفرة إلى صديق:

عزيزي كارين,

    أتمنى أن تكون جيد. هل ما زلنا نتناول العشاء غدا?

    تفضلوا بقبول فائق الاحترام,

    جوامع

دعنا نقول أنك قمت بترميز الرسالة بطريقة بسيطة تغيير كل حرف إلى الحرف الذي يتبعه في الأبجدية. سيؤدي ذلك إلى تغيير الرسالة إلى:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. بسف xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

إذا اعترض أعداؤك هذه الرسالة ، فهناك خدعة يمكنهم استخدامها لمحاولة كسر الشفرة. بامكانهم انظر إلى تنسيق رسالتك وحاول تخمين ما قد تقوله الرسالة. يعلمون أن الأشخاص يبدأون عادة رسائلهم بـ “Hi” أو “Hello” أو “Dear” أو عدد من الاتفاقيات الأخرى.

إذا حاولوا تطبيق كلمة “مرحبًا” أو “مرحبًا” باعتبارها الكلمة الأولى ، فسيجدون أنها لن تتناسب مع عدد الأحرف. ثم يمكنهم تجربة “عزيزي”. يناسب ، ولكن هذا لا يعني بالضرورة أي شيء. كان المهاجمون يحاولون ذلك فقط ويروا أين قادهم. لذلك سيغيرون الأحرف “e” و “f” و “b” و “s” بكلمة “d” و “e” و “a” و “r” على التوالي. هذا من شأنه أن يعطيهم:

عزيزي لاسيو,

    J ipqe zpv هي xemm. هل xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

لا تزال تبدو مربكة للغاية ، لذلك قد يحاول المهاجمون النظر في بعض الاتفاقيات الأخرى, مثل كيف نختتم رسائلنا. غالبًا ما يضيف الأشخاص “من” أو “مع أطيب التحيات” في النهاية ، ولكن لا يتناسب أي منهما مع التنسيق. بدلاً من ذلك ، قد يحاول المهاجمون “تفضلوا بقبول فائق الاحترام” واستبدال الرسائل الأخرى لمعرفة أين يحصل عليها. عن طريق تغيير “z” ، “p” ، “v” ، “t” ، “j” “o” ، “d” و “m” مع “y” ، “o” ، “u” ، “s” ، ” i “و” n “و” c “و” l “على التوالي ، سيحصلون على:

عزيزي لاسين,

    أنا ioqe أنت xell. هل xe tuill iawinh dinnes uonossox?

    تفضلوا بقبول فائق الاحترام,

    Kanet

بعد هذا التعديل ، يبدو أن المهاجمين بدأوا في الوصول إلى مكان ما. لقد وجدوا الكلمات “أنا” ، “أنت” و “أنت” ، بالإضافة إلى الكلمات التي تشكلت التخمينات الأولية.

نظرًا لأن الكلمات في ترتيب نحوي صحيح ، يمكن للمهاجمين أن يكونوا واثقين جدًا من أنهم يتجهون في الاتجاه الصحيح. الآن ، ربما أدركوا أيضًا أن الكود الذي يتضمن كل حرف يتم تغييره إلى الحرف الذي يتبعه في الأبجدية. بمجرد أن يدركوا ذلك ، فإنه يجعل من السهل ترجمة الباقي وقراءة الرسالة الأصلية.

المثال أعلاه كان مجرد رمز بسيط ، ولكن كما ترون, بنية الرسالة يمكن أن تعطي المهاجمين أدلة حول محتواها. بالتأكيد ، كان من الصعب معرفة الرسالة من هيكلها فقط واستغرق الأمر بعض التخمين المتعلم ، لكن عليك أن تضع في اعتبارك أن أجهزة الكمبيوتر أفضل بكثير في القيام بذلك مما نحن عليه الآن.. هذا يعني أنه يمكن استخدامها لمعرفة رموز أكثر تعقيدًا في وقت أقصر بكثير, بناء على القرائن التي تأتي من الهيكل وعناصر أخرى.

إذا كانت البنية يمكن أن تؤدي إلى كسر الشفرة وكشف محتويات الرسالة ، فإننا نحتاج إلى طريقة لإخفاء الهيكل للحفاظ على أمان الرسالة. هذا يقودنا إلى حشوة.

عندما تكون الرسالة مبطنة, تتم إضافة بيانات عشوائية لإخفاء أدلة التنسيق الأصلية التي قد تؤدي إلى كسر رسالة مشفرة. مع RSA ، الأمور أكثر تعقيدًا قليلاً ، لأن المفتاح المشفر ليس به التنسيق الواضح لخطاب ساعدنا في تقديم أدلة في مثالنا أعلاه.

على الرغم من ذلك ، يمكن للخصوم استخدام عدد من الهجمات لاستغلال الخصائص الرياضية لرمز ما وكسر البيانات المشفرة. بسبب هذا التهديد, تستخدم تطبيقات RSA مخططات الحشو مثل OAEP لتضمين بيانات إضافية في الرسالة. إضافة هذه الحشوة قبل تشفير الرسالة يجعل RSA أكثر أمانًا.

توقيع الرسائل

يمكن استخدام RSA لأكثر من مجرد تشفير البيانات. خصائصه تجعله نظامًا مفيدًا أيضًا التأكيد على أن الرسالة قد تم إرسالها من قبل الكيان الذي يدعي أنه قد أرسلها ، بالإضافة إلى إثبات أن الرسالة لم يتم تغييرها أو التلاعب بها.

عندما يريد شخص ما إثبات صحة رسالته ، يمكنه حساب أ مزيج (دالة تأخذ بيانات ذات حجم تعسفي وتحولها إلى قيمة ذات طول ثابت) للنص الشائع ، ثم توقعها باستخدام المفتاح الخاص. هم قم بتوقيع التجزئة من خلال تطبيق نفس الصيغة المستخدمة في فك التشفير (م = جد وزارة الدفاع ن). بمجرد توقيع الرسالة ، يرسلون هذا التوقيع الرقمي إلى المستلم بجانب الرسالة.

إذا تلقى المستلم رسالة ذات توقيع رقمي ، فيمكنه استخدام التوقيع للتحقق مما إذا كانت الرسالة موقعة أصلاً بواسطة المفتاح الخاص للشخص الذي يدعي أنه أرسلها. يمكنهم أيضًا معرفة ما إذا كانت الرسالة قد تم تغييرها بواسطة المهاجمين بعد إرسالها.

للتحقق من التوقيع الرقمي ، يستخدم المستلم أولاً دالة التجزئة نفسها للعثور على قيمة التجزئة للرسالة التي تلقاها. ثم يطبق المستلم المفتاح العام للمرسل إلى التوقيع الرقمي, باستخدام صيغة التشفير (ج = مالبريد وزارة الدفاع ن), لمنحهم التجزئة من التوقيع الرقمي.

بواسطة مقارنة تجزئة الرسالة التي تم استلامها بجانب علامة التجزئة من التوقيع الرقمي المشفر, يمكن للمستلم معرفة ما إذا كانت الرسالة أصلية أم لا. إذا كانت القيمتان متماثلتين ، فلن يتم تغيير الرسالة منذ التوقيع عليها بواسطة المرسل الأصلي. إذا تم تغيير الرسالة بحرف واحد ، فإن قيمة التجزئة ستكون مختلفة تمامًا.

أمن RSA & هجمات

مثل معظم أنظمة التشفير ، يعتمد أمان RSA على كيفية تنفيذه واستخدامه. عامل مهم واحد هو حجم المفتاح. ال كلما زاد عدد البتات في المفتاح (بشكل أساسي طول المدة التي يستغرقها المفتاح) ، زادت صعوبة اختراق الهجمات مثل القسري الغاشمة والعوملة.

نظرًا لأن خوارزميات المفتاح غير المتماثل مثل RSA يمكن كسرها بواسطة عامل صحيح ، بينما لا يمكن لوغاريتمات المفتاح المتماثل مثل AES ، تحتاج مفاتيح RSA إلى أن تكون أطول بكثير لتحقيق نفس المستوى من الأمان.

حاليا ، و أكبر حجم رئيسي تم تحليله هو 768 بت. تم ذلك بواسطة فريق من الأكاديميين على مدار عامين ، باستخدام مئات الآلات.

منذ اكتمال عملية العوملة بحلول نهاية عام 2009 ونمت قوة الحوسبة بشكل كبير منذ ذلك الوقت ، يمكن افتراض أن هناك محاولة لكثافة مماثلة يمكن الآن عامل مفتاح RSA أكبر بكثير.

على الرغم من هذا ، فإن الوقت والموارد اللازمة لهذا النوع من الهجوم يضعه في متناول معظم المتسللين وفي عالم الدول القومية. يعتمد طول المفتاح الأفضل للاستخدام على نموذج التهديد الفردي. المعهد الوطني للمعايير والتكنولوجيا يوصي حجم مفتاح الحد الأدنى من 2048 بت, لكن مفاتيح 4096 بت تستخدم أيضا في بعض الحالات التي يكون فيها مستوى التهديد أعلى.

العوملة هي طريقة واحدة يمكن من خلالها كسر RSA. يمكن لعدد من الهجمات الأخرى كسر التشفير باستخدام كمية أقل من الموارد ، ولكن هذه تعتمد على التنفيذ وعوامل أخرى ، وليس بالضرورة RSA نفسها. بعض هذه تشمل:

هي الأعداد الأولية عشوائية حقا?

تستخدم بعض تطبيقات RSA مولدات الأرقام العشوائية الضعيفة للتوصل إلى الأعداد الأولية. إذا لم تكن هذه الأرقام عشوائية بما فيه الكفاية ، فإنه يسهل على المهاجمين التعامل معها وكسر التشفير. هذه المشكلة يمكن تجنبه عن طريق استخدام مولد أرقام زائفة عشوائي آمن.

الفقراء مفتاح جيل

تحتاج مفاتيح RSA إلى الوقوع ضمن معلمات معينة حتى تكون آمنة. إذا كانت الأعداد الأولية ص و ف قريبة جدا من بعضها البعض ، ويمكن بسهولة اكتشاف المفتاح. وبالمثل ، العدد د التي تشكل جزءًا من المفتاح الخاص لا يمكن أن تكون صغيرة جدًا. قيمة منخفضة تجعل من السهل حلها. من المهم أن تكون هذه الأرقام بطول مناسب للحفاظ على أمان مفتاحك.

هجمات قناة جانبية

هذه هي نوع من الهجوم لا يكسر RSA مباشرة ، ولكن بدلاً من ذلك يستخدم المعلومات من التنفيذ لإعطاء تلميحات للمهاجمين حول عملية التشفير. يمكن أن تشمل هذه الهجمات أشياء مثل تحليل كمية الطاقة التي يتم استخدامها, أو تحليل التنبؤ بالفرع, الذي يستخدم قياسات وقت التنفيذ لاكتشاف المفتاح الخاص.

يُعرف نوع آخر من هجمات القنوات الجانبية بأنه هجوم التوقيت. إذا كان لدى المهاجم القدرة على قياس وقت فك التشفير على كمبيوتر الهدف الخاص به لعدد من الرسائل المشفرة المختلفة, يمكن أن تتيح هذه المعلومات للمهاجم التأكد من المفتاح الخاص للهدف.

تتجنب معظم تطبيقات RSA هذا الهجوم عن طريق إضافة قيمة لمرة واحدة أثناء عملية التشفير ، مما يؤدي إلى إزالة هذا الارتباط. هذه العملية تسمى التعمية التشفير.

هل تشفير RSA آمن للمستقبل?

والخبر السار هو أن RSA تعتبر آمنة للاستخدام ، على الرغم من هذه الهجمات المحتملة. التحذير هو ذلك يجب تنفيذه بشكل صحيح واستخدام مفتاح يقع ضمن المعلمات الصحيحة. كما ناقشنا للتو ، لا يمكن اعتبار التطبيقات التي لا تستخدم الحشو أو استخدام أعداد أولية غير كافية الحجم أو لديها ثغرات أمنية أخرى آمنة.

إذا كنت تريد استخدام تشفير RSA, تأكد من أنك تستخدم مفتاحًا لا يقل عن 1024 بت. يجب على من لديهم نماذج تهديد أعلى الالتزام بمفاتيح 2048 أو 4096 بت إذا كانوا يريدون استخدام RSA بثقة. طالما أنك تدرك نقاط الضعف التي تعاني منها RSA واستخدامها بشكل صحيح ، يجب أن تشعر بالأمان لاستخدام RSA لمشاركة المفاتيح والمهام المماثلة الأخرى التي تتطلب تشفير المفتاح العام.

أنظر أيضا: وأوضح أنواع التشفير الشائعة