ما هي التوقيعات الرقمية وكيف تعمل؟

التواقيع الرقمية تشبه الإصدارات الإلكترونية من التواقيع المكتوبة بخط اليد. أنها تسمح للناس للتحقق من صحة وسلامة البيانات, وكذلك منع الموقّع من أن يتنصل (ينكر) تورطه.

أدت هذه الخصائص إلى اعتماد التواقيع الرقمية في مجموعة واسعة من التطبيقات ، بما في ذلك العديد من بروتوكولات الأمان والبريد الإلكتروني الآمن وإدارة الحقوق الرقمية.

في هذه المقالة ، سوف نناقش ما هي التوقيعات الرقمية, حيث يتم استخدامها ، وكذلك التفاصيل التقنية لاثنين من الخوارزميات الأكثر شعبية, RSA و DSA.

ما هي التوقيعات الرقمية?

كما ذكر أعلاه ، توفر لنا التوقيعات الرقمية ثلاث خصائص مهمة للغاية. هذه هي المصادقة والنزاهة وعدم التنصل.

المصادقة هي عملية التحقق من أن الشخص الذي يرسل رسالة هو في الحقيقة من يقولون ، وليس دجالًا.

ال النزاهة من البيانات أو رسالة يشير إلى ما إذا كان قد وصل في نفس الحالة كما هو الحال عندما تم إرسالها. إذا تم تغيير الرسالة أو العبث بها ، فلم تعد تحتفظ بكاملها.

إذا كانت البيانات أو الرسالة غير repudiable-, وهذا يعني أن مؤلفها لا يمكن أن يعترض على أنهم كانوا الخالق الحقيقي للوثيقة. هذه الخاصية تسلب منانتها المعقولة ، أو عذر “آسف ، صديقي كان يستخدم حسابي”.

طالما لم يتم اختراق المفتاح الخاص للفرد ، يمكن أن توفر التواقيع الرقمية جميع هذه الخصائص الثلاثة للبيانات.

قد تتساءل لماذا نحتاج هذه الخصائص في المقام الأول. دعنا نعود خطوة إلى الوراء والتفكير في كيفية قيامنا بأشياء في لقاء وجها لوجه.

دعنا نقول أنك مدين صديقك مايك 100 دولار. أنت شخص جيد ، لذا فأنت سعيد بتسديده عندما تحصل على المال.

أفضل طريقة للقيام بذلك هي مجرد تقديم فاتورة بقيمة 100 دولار لمايك. لقد عرفته منذ سنوات وتعرف كيف يبدو ، لذلك سيكون من السهل التحقق من هويته وبالتالي التحقق من أنك تعطي المال للشخص المناسب.

إذا كنت شرجيًا بالفعل ، يمكنك التحقق من هويته وجعله يوقع إيصالًا بخط اليد لك. التوقيع على الإيصال يمنحها النزاهة ويجعلها غير قابلة للتنصل.

ماذا لو بدلًا من إجراء المعاملة وجهاً لوجه ، تلقيت مكالمة من شخص يقول إنهم مايك ، ويجب عليك إرسال 100 دولار إلى رقم الحساب 12345678.

“لكنك لا تبدو مثل مايك” ، كما تقول.

“لدي رشح. أرسلها الآن ، أحتاج إلى المال “.

هل ترسل المال؟ على الاغلب لا.

لا توجد طريقة لمعرفة ما إذا كان بالفعل مايك أم رقم الحساب الصحيح. على كل ما تعرفه ، قد يكون محتالًا يحاول سرقة منك. بدلاً من تحويل الأموال على الفور ، سيكون من الأفضل الانتظار حتى ترى مايك حتى تتمكن من إعطائه النقود شخصيًا.

تمامًا كما في السيناريو أعلاه ، نواجه كثيرًا مواقف نحتاج فيها تحقق من هوية الطرف أو سلامة البيانات في العالم على الإنترنت. لهذا السبب ارتفعت التوقيعات الرقمية كآلية يمكنها توفير هذه الخصائص وتسهيل المعاملات الآمنة عبر الإنترنت.

بدونها ، قد لا نعرف من نتحدث إليه ، ولا يمكننا التأكد مما إذا كانت البيانات قد تم العبث بها أم لا ، ويمكن للشخص أن ينكر أنه كان مسؤولاً.

استخدامات التوقيعات الرقمية

هذه الخصائص من التوقيعات الرقمية تجعلها مفيدة في مجموعة واسعة من التطبيقات. غالبًا ما يتم استخدامها من قبل أنفسهم أو بالتزامن مع التشفير في مجموعة من بروتوكولات الأمان المختلفة ، مثل:

• أمن بروتوكول الإنترنت
• SSH
• TLS

كما أنها كثيرا ما تستخدم في إدارة الحقوق الرقمية, في تكنولوجيا blockchain, في ادارة العقود التطبيقات ، كجزء من توزيع البرمجيات, و في المالية.

تاريخ التوقيعات الرقمية

تم طرح فكرة التوقيعات الرقمية لأول مرة من قِبل مصممي التشفير المشهورين ويتفيلد ديفي ومارتن هيلمان في بحثهم عام 1976 اتجاهات جديدة في التشفير. في عام 1978 ، أدخل رونالد ريفست ، عدي شامير ولين أدلمان ، خوارزمية RSA في الرأي العام ، والتي يمكن استخدامها لإنتاج توقيعات رقمية غير آمنة.

استغرق الأمر عقدًا آخر حتى تظهر التواقيع الرقمية في تطبيق واسع الانتشار: إصدار Lotus Notes 1.0 من IBM. ومنذ ذلك الحين فصاعدًا ، بدأت التوقيعات الرقمية تشهد اعتمادًا أوسع مع ظهور تقنيات جديدة وتزايدت الحاجة إلى التحقق من التوثيق والتوثيق عبر الإنترنت.

مقدمة موجزة لتشفير المفتاح العام

قبل الانتقال إلى التوقيعات الرقمية ، من الأفضل تغطية بعض الجوانب المهمة لتشفير المفاتيح العامة, التي تشكل الأساس لكيفية عمل التوقيعات الرقمية.

إذا كنت جديدًا نسبيًا في التشفير ، فإن النظام الذي ستكون أكثر دراية به هو تشفير المفتاح المتماثل. هذا يعني فقط أن نفس المفتاح (الذي يشبه كلمة المرور ، ولكن لديه بعض الاختلافات) يستخدم لتشفير البيانات وفك تشفيرها.

كان تشفير المفتاح العام ثورة ، لأنه ينطوي على ذلك باستخدام مفاتيح منفصلة لعملية التشفير وفك التشفير, مما يؤدي إلى مجموعة من تطبيقات التشفير المختلفة. شكل هذان المفتاحان زوج مفاتيح مكون من المفتاح العمومي والمفتاح الخاص. من الواضح أنه يمكن مشاركة المفتاح العام علنًا ، في حين يجب الحفاظ على سرية المفتاح الخاص حتى يكون النظام آمنًا.

الاستخدامان الأكثر شيوعًا لتشفير المفتاح العام هما التشفير والتوقيعات الرقمية.

التشفير

واحدة من الميزات الرائدة في تشفير المفتاح العام هو ذلك يسمح للأطراف الذين لم يلتقوا مطلقًا بإرسال رسائل إلى بعضهم البعض بسرية. يبحث المرسل عن المفتاح العمومي للمستلم المطلوب (يمكن العثور عليه على خوادم المفاتيح العامة أو على مواقع الويب الشخصية أو ببساطة عن طريق سؤال الفرد) ، ثم يشفر رسالة مع هذا المفتاح ، قبل إرساله إلى المستلم.

المستلم هو الشخص الوحيد الذي يمكنه الوصول إلى الرسالة – على افتراض أن المفتاح الخاص لم يتم اختراقه – عن طريق فك تشفيره باستخدام المفتاح الخاص. على الرغم من استخدام المفتاح العمومي لتشفير الرسالة ، لا يمكن فك تشفيرها إلا بواسطة المفتاح الخاص. إذا أراد المستلم الرد ، فسيجد المفتاح العمومي للمرسل الأصلي ، ثم يكرر العملية.

راجع أيضًا: شرح أنواع التشفير الشائعة

كيف تعمل التوقيعات الرقمية?

كما قلنا ، يتم استخدام التواقيع الرقمية للمصادقة ، لمعرفة ما إذا كان قد تم العبث بالبيانات ، ولتوفير عدم التنصل. هناك مجموعة من الآليات المختلفة التي يمكن استخدامها للتوقيعات الرقمية ، ولكل منها اختلافات بسيطة في كيفية هيكلتها.

بشكل عام ، يجب أن تتكون هذه الخوارزميات من ثلاثة خوارزميات فرعية:

• خوارزمية جيل رئيسي – هذه الخوارزمية يولد زوج مفاتيح عشوائي للمستخدم. يجب أن تلتزم الأرقام المتضمنة في زوج المفاتيح بمعلمات معينة لكي تعتبر آمنة. اثنين من أهم الجوانب هي أن الأرقام عشوائية بما فيه الكفاية وحجم مناسب.
• خوارزمية لتوقيع البيانات – بمجرد أن يكون لدى المستخدم مفاتيحه ، هناك طرق محددة لكيفية تطبيقها على البيانات في عملية التوقيع.
• خوارزمية للتحقق من التوقيع – بالمثل ، التحقق من التوقيع يتبع عملية محددة سلفًا.

لكي يكون نظام التوقيع الرقمي فعالًا ، يجب أن يتم تنظيمه بطريقة:

• البيانات الموقعة باستخدام مفتاح خاص هي تم التحقق منه باستخدام المفتاح العمومي المتطابق مع الشخص نفسه.
• يجب أن يكون من المستحيل بشكل أساسي (باستخدام التكنولوجيا والتقنيات الحالية) صياغة توقيع صالح دون معرفة المفتاح الخاص للفرد.

بعض مخططات التوقيع الرقمي الأكثر شيوعًا تشمل RSA و DSA و EcDSA و EdDSA.

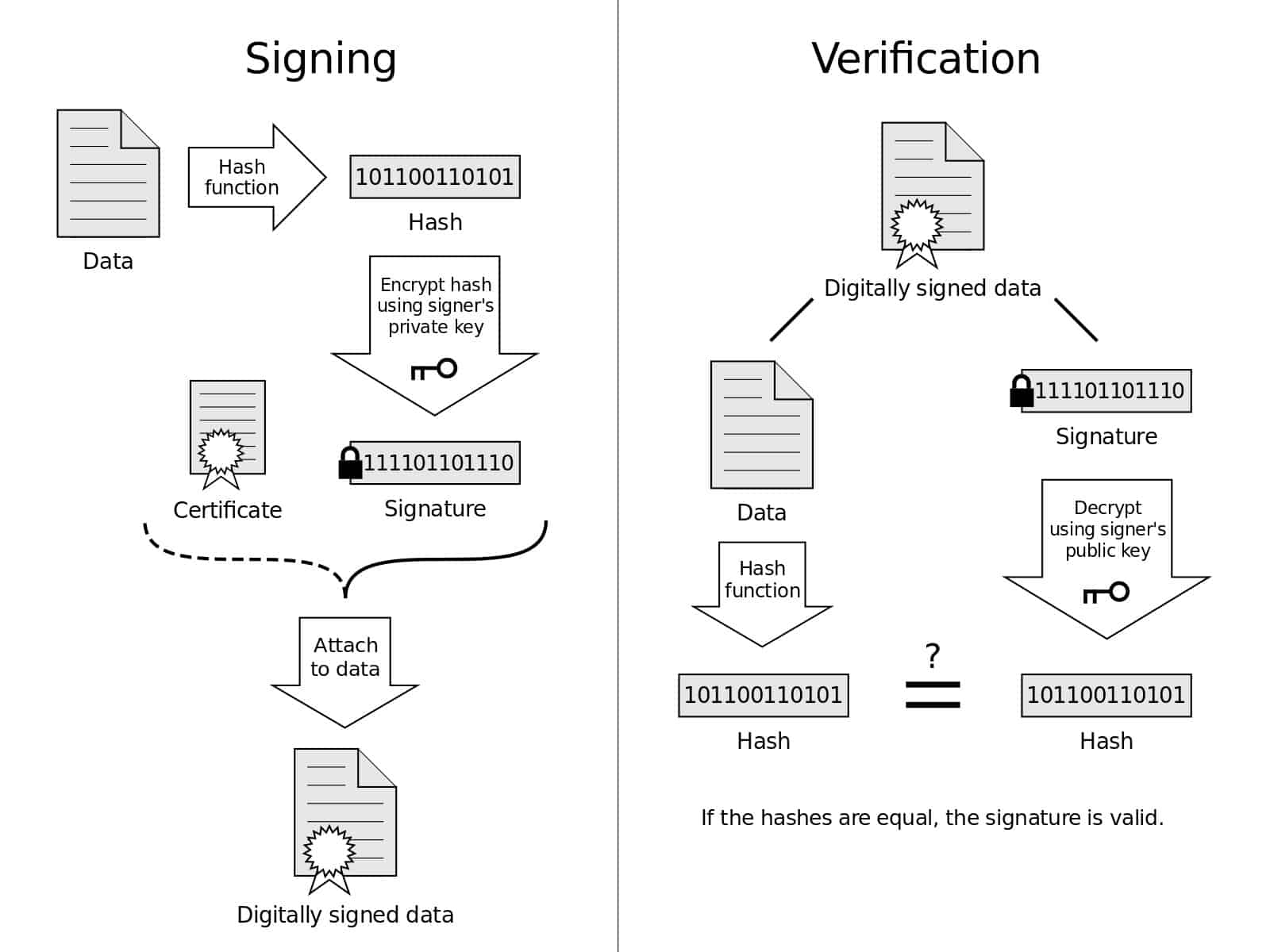
تقدم هذه الصورة تمثيلًا مرئيًا لعمليات التوقيع والتحقق. مخطط التوقيع الرقمي بواسطة Acdx مرخص تحت CC0

RSA

كان RSA أول خوارزمية توقيع رقمي ، ولكن يمكن استخدامه أيضًا لتشفير المفتاح العمومي. في هذه المقالة ، سنتخطى جانب التشفير ، ولكن يمكنك معرفة المزيد عنه في مقالتنا الشاملة التي تغطي ماهية RSA وكيف تعمل.

RSA جيل المفتاح

في تطبيقات آمنة من RSA ، سيتم إنشاء أزواج المفاتيح تلقائيًا وفقًا للعملية التالية:

جيل رئيس

يتم اختيار رقمين أوليين فرديين, ص و ف. سوف يختلف الحجم الدقيق لهذه الأعداد الأولية حسب حجم المفتاح. في هذه الأيام ، يوصى باستخدام مفاتيح RSA 2048 كحد أدنى لتوفير الأمان الكافي ، لذلك نحن نتحدث عن رقمين أوليين يتكاثران لإنتاج رقم 2048 بت.

2048 بت هو حجم في نظام الأرقام الثنائية. إذا تم تحويل عدد من هذا الحجم إلى نظامنا العشري الأكثر مألوفًا ، فسيكون هذا طويلًا تقريبًا:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

يجب اختيار الأعداد الأولية في RSA بشكل عشوائي ويجب أن يكون لها أطوال مماثلة.

في مثالنا ، سوف نستخدم أرقامًا أصغر بكثير لتسهيل فهم الأمور. انتبه إلى أن استخدام مفاتيح بهذا الحجم سيجعل التواقيع الرقمية تافهة. هذا هو السبب في استخدام هذه القيم الكبيرة في الممارسة العملية.

دعنا نقول ما يلي:

ص = 13

ف = 17

ستكون الخطوة الأولى لحساب المعامل ن باستخدام الصيغة التالية:

ن = pq

ن = 13 × 17

ن = 221

قيمة ال ن هو أيضا طول المفتاح.

وظيفة كارمايكل الكاملة

الآن أن لدينا قيمة ل ن, الخطوة التالية هي استخدام وظيفة Carmichael الكاملة:

λ(ن) = لكم] (ص – 1, ف – 1)

هناك بعض الأشياء التي تحتاج إلى فهمها:

• λ(ن(تعني كلمة كارمايكل لقيمة ن
• لكم] يمثل أدنى مضاعف مشترك. هذا هو أقل عدد مشترك على حد سواء ف 1 و ف-1 يمكن أن تنقسم إلى

دعنا ندمج أرقامنا في المعادلة:

λ(221) = لكم] (13 – 1 ، 17 – 1)

λ(221) = لكم] (12 ، 16)

إذا كنت جيدًا في الرياضيات الذهنية ، فربما تكون قد فهمت ذلك 48 هو أدنى مضاعف مشترك على حد سواء 12 و 16. هذا لأن 48 هو أصغر رقم يمكن أن يصلح كلا هذين الرقمين (12 × 4 = 48 ، 16 × 3 = 48). وبالتالي:

λ(221) = 48

الخروج مع المفتاح العمومي

في RSA ، يتكون المفتاح العمومي من القيمة ن (والتي حسبناها بالفعل باسم 221) و البريد. بما أن المفتاح العمومي مشترك بحرية ، فإن القيمة لـ البريد لا يجب أن يكون سراً. في الواقع ، يتم تعيينها في كثير من الأحيان على 65537 في الممارسة ، لأن أعداد أكبر من شأنها أن تبطئ عملية التشفير. في مثالنا ، سنقوم بتعيين البريد الى 5, فقط لجعله عدد صغير وبسيط للعمل مع.

لذلك ، يتكون المفتاح العمومي لهذا المثال من 221 و 5. سنغطي تفاصيل كيفية تطبيق المفتاح العمومي في الأقسام التالية.

معرفة المفتاح الخاص

مثلما يتكون المفتاح العمومي من رقمين ، فإن المفتاح الخاص بنا أيضًا. تتكون المفاتيح الخاصة من د و البريد. نحن نعرف بالفعل قيمة ل البريد (5), ويمكننا استخدام الصيغة التالية للعثور عليها د:

د = 1 /البريد عصري λ(ن)

لاحظ أن عصري فقط يرمز إلى عملية modulo ، مما يعني عادة أنه يجب عليك العثور على الباقي بمجرد تقسيم الجانب الأيسر على اليمين. كمثال:

17 وزارة الدفاع 3 = 2

وذلك لأن 3 تناسبها في 17 ما مجموعه 5 مرات ، مع ما تبقى من 2.

مثالنا مختلف قليلاً. ال “1 /البريد عصريقد يبدو الجزء “من المعادلة يخبرك بالقسمة 1 بواسطة البريد, لكنها في الحقيقة ليست كذلك. إنه أمر محير ، لكن هذه طريقة لتمثيل معكوس وحدات. المعادلة تخبرنا فعلاً بحساب معكوس المعياري لـ البريد و λ(ن).

عادةً ما يتم اشتقاق المعياري المعياري باستخدام خوارزمية Euclidean الموسعة ، لكننا لن نغطي ذلك في هذه المقالة. بدلاً من ذلك ، سوف نستخدم آلة حاسبة على الإنترنت لتسهيل الأمور.

الآن وقد تخلصنا من هذا الأمر ، دعنا ندخل قيمنا في الصيغة:

د = 1/5 وزارة الدفاع 48

لايجاد د, كل ما يتعين علينا القيام به هو إدخال قيمة لدينا ل البريد (5) في الآلة الحاسبة على الإنترنت حيث تقول عدد صحيح, ثم قيمة لدينا ل λ(ن), الذي 48, حيث تقول مودولو.

هذا يعطينا نتيجة ل 29 وفقا لآلة حاسبة على الانترنت. لذلك ، سيتكون المفتاح الخاص بنا من:

البريد = 5

د = 29.

الآن وبعد أن أنشأنا كلا مفتاحينا ، فإن السؤال التالي هو: “ماذا نفعل بهم؟” حسنًا ، يمكننا استخدامها لتشفير الرسائل وفك تشفيرها من خلال تشفير المفتاح العام ، لكن هذه المقالة تتعلق بالتوقيعات الرقمية ، لذلك سوف نركز على ذلك.

توقيع البيانات رقميا مع RSA

دعنا نقول أن شخصًا ما يريد إرسال رسالة إلى صديقه ، ولكنه يريد التأكد من أن الصديق يمكنه التحقق من صحة الرسالة وتكاملها. يمكنهم القيام بذلك باستخدام توقيع رقمي RSA لتوقيع الرسالة.

الخطوة الأولى هي تشغيل الرسالة بأكملها من خلال وظيفة التجزئة. هذه وظائف أحادية الاتجاه توفر دائمًا نفس الإخراج لمدخلات معينة. من المستحيل عكس وظائف التجزئة الآمنة ، مما يعني أنه لا يمكن استخدام الإخراج لمعرفة المدخلات. من غير الممكن أيضًا أن يكون لرسالتين منفصلتين نفس الإخراج.

يمكنك معرفة المزيد عن وظائف التجزئة في ما هو التجزئة? قسم من مقالتنا, التشفير ، التجزئة ، التمليح – ما هو الفرق?

دعنا نقول أننا نريد توقيع الرسالة رقميا “الجو حار اليوم“حتى يتمكن المستلم لدينا من معرفة ما إذا كانت الرسالة أصلية أم لا وما إذا تم العبث بها. لذلك سوف نركض “الجو حار اليوم“من خلال وظيفة التجزئة.

فهم وظائف التجزئة

في هذه الأيام ، تكون دالة التجزئة الآمنة الأكثر شيوعًا هي SHA-256. عندما نضع رسالتنا عبر آلة حاسبة SHA-256 عبر الإنترنت ، فإنها تمنحنا نتيجة مثل هذه:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

هذا يثير بعض المشاكل على سبيل المثال لدينا. الأول هو أنه ليس رقمًا عشريًا مثل الرقم الذي اعتاد عليه معظم الأشخاص. ربما لاحظت أن هناك أحرف في هذا الرقم ، وأنها ترتفع فقط F. هذا يعطينا فكرة أنه في الحقيقة رقم سداسي عشري.

ال يعتمد النظام السداسي عشر على قاعدة 16 ، بدلاً من قاعدة 10, مثل نظام الأرقام التي نستخدمها عادة. هذا يعني أنه بدلاً من العد بمضاعفات 10 ، يتم حسابه في مضاعفات 16 ، ويتم استخدام الأحرف الستة الأولى من الأبجدية لتعويض هذه الأرقام الإضافية. يمكن تحويل عدد مثل هذا إلى نظامنا العشري اليومي ، ولكن هذا خارج عن نطاق هذه المقالة.

المسألة الثانية التي لدينا هي أن هذا هو عدد كبير حقا. إذا تم تحويله إلى رقم عشري ، فسيكون أطول. نظرًا لأننا نهدف إلى البساطة في هذا الدليل ، فإن إجراء العمليات الحسابية باستخدام هذا العدد الكبير من شأنه أن يجعل الأمور مربكة للغاية بحيث يتعذر الوصول إلى المفاهيم الأساسية عبر.

مع فكرة إظهار كيفية عمل التواقيع الرقمية RSA بطريقة يسهل فهمها ، فلن نستخدم قيمة التجزئة الكبيرة في المثال التالي. بدلاً من ذلك ، سوف ندعي أن قيمة التجزئة “الجو حار اليوم” هو ببساطة 10.

سيتعين علينا أيضًا التظاهر ، مثله مثل أي تجزئة حقيقية ، كلما وضعنا مدخلاتنا لـ “أصبح الجو حارًا اليوم” من خلال دالة التجزئة ، فستظهر دائمًا قيمة 10. لكي تكون متسقًا مع الطريقة التي تعمل بها وظائف التجزئة ، سيتعين علينا أن ندعي أنه من غير المحتمل أن يعطي أي مدخلات أخرى القيمة نفسها. وبالمثل ، نحتاج إلى التظاهر بأنه ليس من الممكن أيضًا معرفة مدخلاتنا الأصلية من هذه القيمة. هذه الخصائص هي التي تجعل التجزئة مفيدة للغاية.

كيفية استخدام المفتاح الخاص للمرسل للتوقيع رقمياً على قيمة التجزئة

قام مرسلنا بكتابة رسالته ، ثم وضعها في دالة هاش ، والتي نتظاهر أنها أعادت قيمة 10. بمجرد حصول المرسل على تجزئة الرسالة ، يمكنه إنشاء التوقيع الرقمي من خلال تطبيق المفتاح الخاص على قيمة التجزئة بالصيغة التالية:

م (ج) = جد عصري ن

هذه هي في الواقع صيغة فك تشفير البيانات التي تم تشفيرها باستخدام المفتاح العمومي للمستلم ، ولكنها تُستخدم أيضًا لتوقيع المستندات رقميًا.

عندما يتعلق الأمر بالتوقيعات الرقمية:

• قيمة ال م (ج) سوف يكون التوقيع.
• قيمة ال ج هو تجزئة الرسالة (10).
• قيمة ال د جزء من المفتاح الخاص للمرسل ، والذي استخلصناه سابقًا (29).
• ال عصري الوظيفة هي نفس العملية المتبقية التي قمنا بتغطيتها مسبقًا.
• قيمة ال ن هو الجزء الآخر من المفتاح الخاص للمرسل ، والذي قمنا بحسابه في البداية (221).

لذلك ، دعونا نضع كل شيء في صيغتنا:

م (ج) = 1029 وزارة الدفاع 221

    م (ج) = 100،000،000،000،000،000،000،000،000،000 mod 221

دعنا ندير هذا من خلال آلة حاسبة مودولو التالية (أوضحنا كيف تعمل هذه العمليات في إطار معرفة المفتاح العمومي الجزء). لكي يعمل بشكل صحيح ، نحتاج إلى تعيين مدخلاتنا على النحو التالي:

• رقم أ اكتب – عدد عشري
• رقم أ القيمة – 100000000000000000000000000000
• رقم ب اكتب – عدد عشري
• رقم ب القيمة – 221
• معادلة الحساب (هذا هو فقط الكود الذي يخبر الآلة الحاسبة بالتشغيل الذي يجب القيام به. ويمكن العثور على هذه الرموز وغيرها في صفحة الويب المرتبطة أعلى قسم الإدخال) – وزارة الدفاع (أ، ب)

إذا كنت قد فعلت الأشياء بشكل صحيح ، فيجب أن تبدو كما يلي:

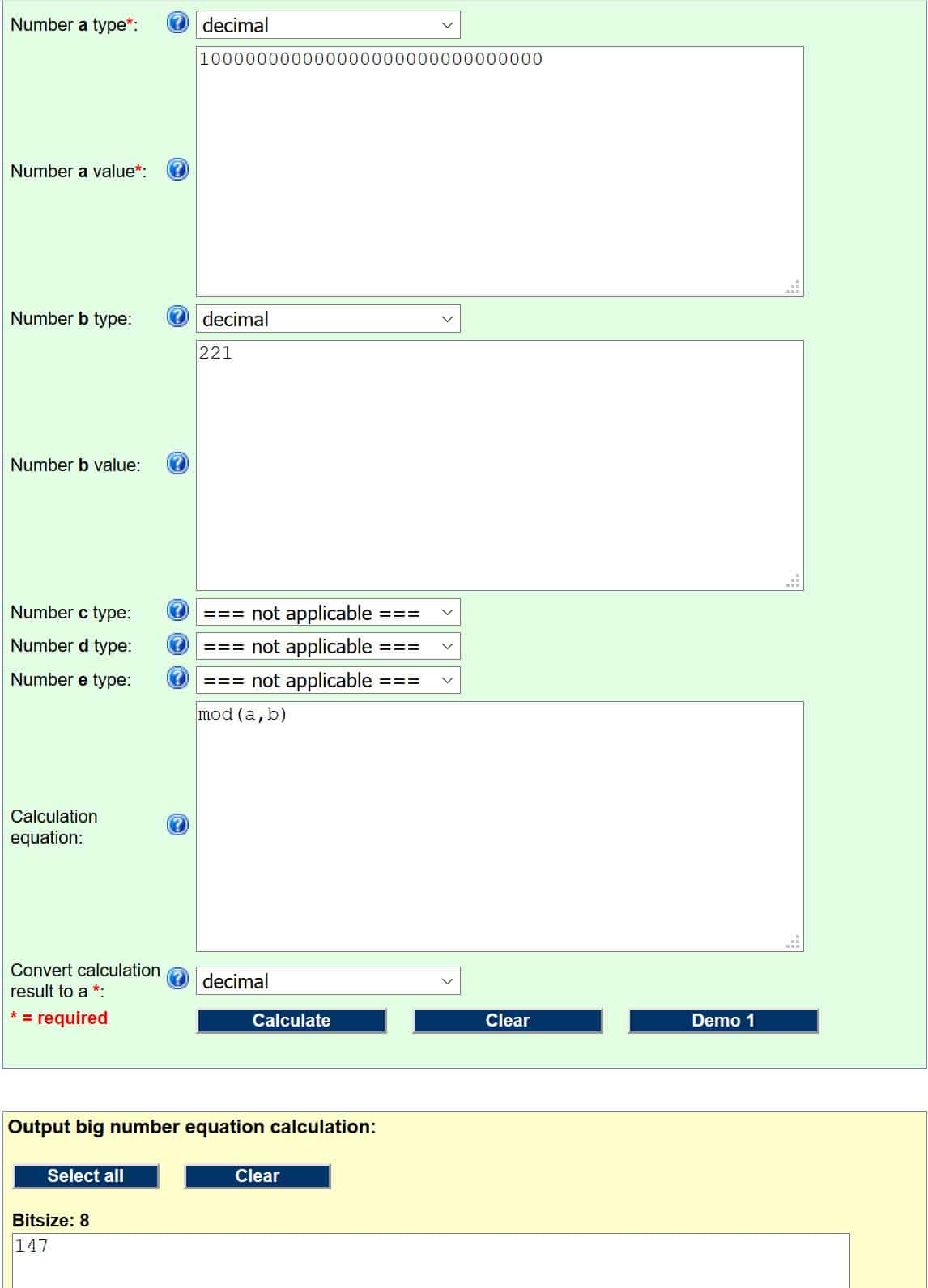
الرقم في المربع الأصفر هو إجابتنا ، وبالتالي فإن التوقيع الرقمي للتجزئة للرسالة هو 147.

لإثبات صحة الرسالة وتكاملها ، إلى جانب توفير عدم التنصل ، يقوم مرسلنا بإرسال الرسالة “الجو حار اليوم“جنبا إلى جنب مع التوقيع الرقمي لل 147 إلى المستلم المطلوب. فقط تذكر أننا استخدمنا قيمة صغيرة للتجزئة لتبسيط الأشياء ، بدلاً من التجزئة الحقيقي للرسالة.

التحقق من التوقيعات الرقمية

التواقيع الرقمية مفيدة فقط إذا استطعنا التحقق مما إذا كانت شرعية أم لا. طالما لم يتم اختراق المفتاح الخاص للمرسل ، يمكن للمستلم اختبار ما إذا كانت الرسالة أصلية وتحافظ على سلامتها من خلال تطبيق الصيغة التالية على التوقيع الرقمي:

    سم) = مالبريد عصري ن

في عكس عملية التوقيع ، هذه هي في الواقع الصيغة المستخدمة لتشفير البيانات في RSA. عندما نستخدم هذه الصيغة للتحقق من التوقيعات:

• قيمة ال سم) ستكون قيمة تجزئة المرسل في وقت توقيعه (بسبب بنية خوارزمية المفتاح العمومي RSA ، سيؤدي تطبيق المفتاح العام للمرسل من خلال هذه الصيغة إلى التراجع عن عملية التوقيع التي أجريناها للتو ، مما يتركنا مع تجزئة التظاهر الأصلية لدينا ).
• قيمة ال م هو التوقيع الرقمي (147).
• قيمة ال البريد جزء من المفتاح العام للمرسل ، والذي استخلصناه سابقًا (5).
• ال عصري الوظيفة هي نفس العملية المتبقية التي قمنا بتغطيتها مسبقًا.
• قيمة ال ن هو الجزء الآخر من المفتاح العمومي للمرسل ، والذي قمنا بحسابه في البداية (221).

دعنا نلقي كل ذلك في الصيغة:

    سم) = 1475 وزارة الدفاع 221

    سم) = 68،641،485،507 وزارة الدفاع 221

دعونا نستخدم نفس آلة حاسبة modulo كما كان من قبل ونحافظ على كل شيء كما هو ، باستثناء:

• رقم أ القيمة – 68641485507

إذا قمت بإدخال الأشياء بشكل صحيح ، فيجب أن تحصل على نتيجة:

سم) = 10

الآن بعد أن قام المستلم بحساب قيمة التجزئة من التوقيع الرقمي ، فإن الخطوة التالية هي حساب قيمة التجزئة للرسالة التي تلقوها ، “الجو حار اليوم“. إذا كنت تتذكر من قبل ، فلن نستخدم فعليًا تجزئة SHA-256 الحقيقية للرسالة ، لأن الرقم كان كبيرًا جدًا وجعل المثال معقدًا للغاية.

بدلاً من ذلك ، كنا نتظاهر بأن دالة التجزئة أعطتنا بالفعل عددًا صغيرًا, 10, لمساهماتنا. نظرًا لأن دالات التجزئة تقوم دائمًا بإخراج نفس النتيجة لمدخل معين ، عندما يضع المستلم لدينا “الجو حار اليوم“من خلال دالة التجزئة الوهمية الخاصة بنا ، فقد تلقوا أيضًا قيمة 10.

ينتج عن عملية التحقق من التوقيع قيمتين. القيمة الأولى هي التجزئة كما كانت عندما قام المرسل بالتوقيع عليها رقميًا باستخدام المفتاح الخاص. حسبنا ذلك أعلاه باستخدام المفتاح العمومي للمرسل.

القيمة الثانية هي تجزئة الرسالة التي تلقاها المستلم. يتم حساب ذلك باستخدام نفس دالة التجزئة التي استخدمها المرسل لتجزئة رسالته الأصلية. ثم تتم مقارنة هاتين القيمتين ، وإذا كانت القيمتان متماثلتين ، فيمكننا افتراض أن الرسالة أصلية وتحتفظ بكاملها وأنها غير قابلة للتنصل. بالطبع ، هذا يفترض أن المفتاح الخاص للمرسل لم يتم اختراقه.

منذ مثالنا عاد قيمة 10 للتجزئة عندما تم التوقيع عليها من قبل المرسل ، وكذلك قيمة 10 كما تجزئة الرسالة التي وردت ، يمكننا أن نفترض أن الرسالة ، “الجو حار اليوم” يأتي من الشخص الذي يدعي أنه قد أرسله ، وأنه لم يتغير منذ إرساله.

إذا أراد المستلم الرد حتى يتسنى لمراسله التحقق من رسالته بنفس الطريقة ، يتم تكرار العملية برمتها ، باستثناء المفاتيح الخاصة والعامة للمستلم تستخدم في عمليات التوقيع والتحقق ، على التوالي.

كل هذا الرياضيات قد وضعك قبالة فكرة كاملة من التوقيعات الرقمية. لا تقلق ، لأن تطبيقات RSA تقوم بأتمتة هذه العملية ، لذلك لا يتعين عليك تحطيم أي أرقام.

إيجابيات RSA & سلبيات

RSA هي واحدة من خوارزميات التوقيع الرقمي الأكثر دعمًا وتطبيقًا ، على الرغم من وجود تحرك نحو الخوارزميات الأحدث والأكثر كفاءة والأمان مثل ECDSA و EdDSA.

بالمقارنة مع DSA (التي سنغطيها في القسم التالي) ، تكون RSA أسرع في التحقق من التوقيعات ، ولكنها أبطأ في توليدها. نظرًا لأن التواقيع تميل إلى التأسيس مرة واحدة والتحقق منها عدة مرات ، فإن RSA مفضل عمومًا على DSA.

DSA

يستند أمان خوارزمية التوقيع الرقمي إلى مفهومين رياضيين ، وهما مشكلة اللوغاريتم المنفصلة ، وبعض خصائص الأس الأسي المعياري. بالنسبة لبعض المجموعات ، لا يمكن حساب اللوغاريتمات المنفصلة الخاصة بها مع التقنيات والتقنيات الحالية.

جيل مفتاح DSA

لإنشاء مفاتيح DSA ، تتمثل الخطوة الأولى في اختيار المعلمات التي يمكن لمجموعة من المستخدمين في نفس النظام استخدامها لإنشاء زوج مفاتيح.

توليد المعلمات

• اختيار أ دالة تجزئة – SHA-256 هو الخيار الأكثر شيوعًا لتلبية متطلبات الأمان الحديثة.
• يستقر على أطوال المفاتيح, L و ن – هذه الأيام, L يجب أن يكون طولها 2048 بت على الأقل ن يجب أن يكون 256 بت على الأقل.
• اتخاذ قرار بشأن رئيس الوزراء, ف, هذا هو نفس طول ن.
• اختر رئيس الوزراء, ص, أين ص-1 مضاعف ف.
• اختر رقما, ز, باستخدام الصيغة التالية (أين ح هو رقم تعسفي بين 1 و ف 1):

ز = ح(ص – 1) /ف عصري ص

عادةً ما تكون هذه القيم أرقامًا كبيرة جدًا من أجل جعل الخوارزمية آمنة. لمنع مثالنا من صعوبة حسابه أو شرحه ، سنستخدم أرقامًا أصغر بكثير لن تكون آمنة في الواقع. دعنا نقول ما يلي:

    ف = 5

    ص = 11

لايجاد ز, نقوم بتوصيل أرقامنا في الصيغة. سوف نستخدم 3 كقيمة لدينا ل ح:

ز = 3 (11-1) / 5 mod 11

ز = 32 وزارة الدفاع 11

ز = 9 وزارة الدفاع 11

سنستخدم نفس الآلة الحاسبة كما في كيفية استخدام المفتاح الخاص للمرسل للتوقيع رقمياً على قيمة التجزئة الجزء. المعلمات ستكون هي نفسها ، باستثناء:

• رقم أ القيمة – 9
• رقم ب القيمة – 11

إذا قمت بإدخال كل شيء بشكل صحيح ، فسوف يمنحك نتيجة لذلك ز من 9.

توليد مفاتيح المستخدم

ثم يأخذ المستخدمون الأفراد هذه المعلمات ويستخدمونها لتشكيل زوج المفاتيح الخاص بهم:

• المفتاح الخاص (س) هو رقم بينهما 0 و ف, التي وضعناها في 5. على سبيل المثال لدينا ، وسوف نختار 2 أن يكون س, مفتاحنا الخاص.
• المفتاح العمومي (ذ) تحسب باستخدام الصيغة التالية:

    ذ = زس عصري ص

وبالتالي:

ذ = 92 وزارة الدفاع 11

ذ = 81 وزارة الدفاع 11

سوف نستخدم نفس الآلة الحاسبة modulo مرة أخرى. المعلمات ستكون هي نفسها ، باستثناء:

• رقم أ القيمة – 81
• رقم ب القيمة – 11

إذا قمت بإدخال الأشياء بشكل صحيح ، فيجب أن تحصل على نتيجة ص = 4. المفتاح العمومي لذلك 4.

الآن وقد أنشأنا كل قيمنا ، فلنمنحك خلاصة سريعة. المعلمات للنظام هي:

• ص = 11
• ف = 5
• ز = 9

يتكون زوجنا الرئيسي من:

• المفتاح الخاص, س = 2
• المفتاح العمومي, ذ = 4

توقيع البيانات رقميا مع DSA

يمكن للمرسلين استخدام مفتاح DSA الخاص بهم لتوقيع البيانات رقميًا ، مما يسمح للمستلمين بالتحقق من صحة الرسالة والحفاظ على سلامتها. كما يمنع المرسل من التمكن من التنصل من الرسالة.

تبدأ عملية التوقيع عن طريق إنشاء قيمة عشوائية ك, وهو بين 1 و ف. في هذا المثال ، دعنا فقط نختار 3 كرقم عشوائي لدينا, ك.

ثم نتبع الصيغة التالية لإنشاء مفتاح فردي (ص) للرسالة:

ص = (زك عصري ص) وزارة الدفاع ف

لنرمي أرقامنا:

ص = (93 mod 11) mod 5

ص = (729 mod 11) mod 5

نحن نستخدم لدينا آلة حاسبة modulo مرة أخرى 729 و 11, الذي يعطينا نتيجة ل 3. وبالتالي:

ص = 3 وزارة الدفاع 5

ثم نكرر عملية modulo مرة أخرى مع القيم الجديدة لمنحنا:

ص = 3

قيمة لدينا ل ص يستخدم كمفتاح للرسالة.

لقد توصلنا إلى الجزء الآخر من التوقيع الرقمي, س, مع الصيغة التالية:

س = ك-1(H(م) + XR) عصري ف

ال ك-1 لا يمثل أخذ القوة السلبية ل ك, ولكن بدلا من ذلك حساب معكوس وحدات ، تماما مثل في منطقتنا معرفة القسم الفرعي الخاص بالمفتاح في الجزء السابق من المقال حيث تحدثنا عن RSA.

H(م) هي قيمة التجزئة للرسالة التي يوقعها المرسل. عادة ، ستكون هذه قيمة تجزئة طويلة مشتقة من الرسالة ، تمامًا كما هو الحال في فهم قيم التجزئة القسم الفرعي أعلاه ، والذي قمنا بتغطيته عندما كنا نتحدث عن خوارزمية RSA.

على سبيل المثال ، سنبقي الأمور بسيطة. مثلما هو الحال في قسم RSA ، سنقول أن رسالتنا, م, يكون “الجو حار اليوم“ وأن تجزئة الرسالة H(م) ، هو 10.

لذلك دعونا ندخل جميع قيمنا في الصيغة:

س = 3-1 (10 + 2 × 3) (mod 5)

س = 3-1 (10 + 6) (mod 5)

س = 3-1 (16) (تعديل 5)

الآن ، نأخذ معكوس وحدات 3 لترتيب 5 (لان 5 هي قيمتنا ل ف) ، باستخدام نفس الآلة الحاسبة معكوس من السابق. أدخل 3 كما عدد صحيح و 5 كما معامل ، والتي سوف تعطيك نتيجة ل 2. وبالتالي:

س = 2 (16) (وزارة الدفاع 5)

س = 32 (وزارة الدفاع 5)

دعنا نعود إلى الآلة الحاسبة الخاصة بنا من أجل تشغيل المعامل العادي ، مع الحفاظ على نفس المعلمات التي استخدمناها سابقًا ، باستثناء:

• رقم أ القيمة – 32
• رقم ب القيمة – 5

إذا كنت قد فعلت هذا بشكل صحيح ، فسوف يعطي قيمة ل س من 2. التوقيع الرقمي يتكون من ص و س (3 و 2 على التوالي). يرسل المرسلون التوقيع الرقمي إلى مستلمهم إلى جانب رسالتهم ، “الجو حار اليوم“. سوف يشاركون أيضًا قيم ص ، ف, ز و ذ مع المتلقي.

التحقق من التوقيعات الرقمية

عندما يتلقى المستلم التوقيع الرقمي بجانب الرسالة ، يمكنه التحقق من سلامة الرسالة ومصداقيتها من خلال مجموعة الحسابات التالية.

الخطوة الأولى هي العثور على تجزئة الرسالة التي تلقوها. يقوم المستلم بذلك عن طريق تشغيل الرسالة بالكامل من خلال دالة تجزئة. للحفاظ على الأشياء بسيطة ومتسقة ، دعنا نقول أن تجزئة الرسالة, H(مهو 10.

كما تم إرسال المستلم القيم التالية ، والتي يستخدمونها في عملية التحقق:

• التوقيع الرقمي (ص ، ق) – 3 ، 2
• ص – 1
• ف – 5
• ز – 9
• ذ – 4

الحساب الأول هو العثور عليها ث:

ث = س-1 وزارة الدفاع ف

مرة أخرى ، و س-يمثل 1 أخذ معكوس وحدات. دعنا ندخل قيمنا:

ث = 2-1 وزارة الدفاع 5

سوف نستخدم الآلة الحاسبة العكسية المعيارية من السابق. أدخل 2 كما عدد صحيح و 5 كما معامل ، والتي سوف تعطيك نتيجة ل 3 إلى عن على ث. والخطوة التالية هي العثور عليها ش1 بالصيغة التالية:

ش1 = H(م) س ث عصري ف

دعنا نلقي بقيمنا:

ش1 = 10 × 3 وزارة الدفاع 5

ش1 = 30 وزارة الدفاع 5

العودة إلى آلة حاسبة modulo العادية ، مع الحفاظ على نفس المعلمات التي استخدمناها سابقًا ، باستثناء:

• رقم أ القيمة – 30
• رقم ب القيمة – 5

هذا يعطينا نتيجة ل 0 ل ش1.

نحن نستخدم الصيغة التالية للتوصل إلى ش2:

ش2 = ص س ث عصري ف

دعنا ندخل أرقامنا:

ش2 = 3 × 3 وزارة الدفاع 5

ش2 = 9 وزارة الدفاع 5

بعد ذلك ، نعود إلى آلة حاسبة modulo العادية ، باستخدام نفس المعلمات كما سبق ، باستثناء:

• رقم أ القيمة – 9
• رقم ب القيمة – 5

إذا قمت بإدخال هذا بشكل صحيح ، فسوف يمنحك نتيجة ش2 من 4.

الآن أن لدينا قيمنا ل ش1 و ش2, نستطيع إيجاد الخامس, مع الصيغة التالية:

ت = (زU1ذU2 عصري ص) عصري ف

لنرمي أرقامنا:

الخامس = (90 × 44 وزارة الدفاع 11) وزارة الدفاع 5

الخامس = (1 × 256 mod 11) mod 5

الخامس = (256 mod 11) mod 5

نعود إلى حاسبة المودولو العادية لدينا ، باستخدام نفس المعلمات كما سبق ، باستثناء:

• رقم أ القيمة – 256
• رقم ب القيمة – 11

هذا يعطينا نتيجة ل 3. وبالتالي:

الخامس = 3 وزارة الدفاع 5

ثم نستخدم حاسبة المودولو العادية مرة أخيرة ، مرة أخرى بنفس المعلمات ، باستثناء:

• رقم أ القيمة – 256
• رقم ب القيمة – 11

هذا يعطينا نتيجة ل الخامس من 3.

إذا كانت الرسالة أصلية ولم يتم العبث بها ، v ستكون مساوية r:

    ت = 3

    ص = 3

    3 = 3

لذلك تم إرسال الرسالة من قبل صاحب المفتاح الخاص ، ولم يتم تغيير الرسالة منذ توقيعها.

الايجابيات DSA & سلبيات

يعتمد أمان DSA على ما إذا كان يستخدم أرقامًا كافية. بالإضافة إلى ص ، ف و ز الالتزام المعلمات الصحيحة ، وقيمة ك يحتاج أيضا إلى أن تكون عشوائية. لا ينبغي أن تكون قيمة يمكن التنبؤ بها ، أو قيمة تُستخدم عدة مرات. إذا لم يتم تلبية هذه المتطلبات ، فيمكن للمهاجم استرداد المفتاح.

رغم هذا الاحتمال, يعتبر DSA عمومًا آمنًا طالما تم تنفيذه بشكل صحيح ويستخدم قيمًا مناسبة. على الرغم من أنها آمنة نسبيًا ، إلا أنه لا يتم تطبيق DSA كثيرًا بالمقارنة مع RSA أو أساليب التوقيع الرقمي الأخرى. عند مقارنتها بـ RSA ، يمكنها إنشاء مفاتيح بشكل أسرع وأسرع أيضًا في توليد التواقيع الرقمية ، ولكنها أبطأ في التحقق منها.

توقف الإصدار 7.0 من OpenSSH عن دعم مفاتيح DSA افتراضيًا ، مما يبدو أنه علامة على أن العالم يتخطى DSA ويعمل على خوارزميات أخرى.

ECDSA & EdDSA

ليست RSA و DSA خوارزميات التوقيع الرقمي الوحيدة ، كما أنها ليست الأنسب لجميع المواقف. هناك مجموعة من الآخرين ، مثل ECDSA و EdDSA, التي لها خصائص تجعلها مفضلة في ظروف معينة.

لسوء الحظ ، تعتمد هذه على الرياضيات الأكثر تعقيدًا ، مثل منحنى إهليلجي وتشفير منحنى إدواردز. لن نغطيها بالتفصيل اليوم بسبب هذا التعقيد الإضافي ، لكننا سنتحدث عن بعض إيجابياتها وسلبياتها المحتملة.

ECDSA

تعد خوارزمية التوقيع الرقمي للناحية الاهتزازية من أشكال DSA التي تتضمن تشفير منحنى إهليلجي. يوفر مستوىً مشابهاً من الأمان لـ RSA ، ولكن باستخدام مفتاح أصغر بكثير. هذا يجعلها أكثر فعالية من RSA أو DSA في معظم جوانب الأداء.

EdDSA

هذا بديل DSA آخر ، إلا أنه يعتمد على منحنيات Twisted Edwards. إنه جديد نسبيًا بقدر ما تذهب الخوارزميات ، التي لها مزاياها وعيوبها. على الجانب الإيجابي ، فإنه يستخدم تقنيات أحدث تضيف إلى أدائه.

لسوء الحظ ، لم تتعرض الخوارزميات الحديثة لمزيد من التدقيق ، لذلك كثير من الناس يتوخون الحذر عند اتخاذ قرار بشأن تنفيذها أم لا..

على الرغم من هذا ، واستخدام يوفر EdDSA مستوى عالٍ من الأداء, مقاومة هجمات القنوات الجانبية ، ويلغي الحاجة إلى رقم عشوائي فريد في كل توقيع. في هذه المرحلة ، تبدو EdDSA واعدة وبدأت في رؤية تطبيق أوسع ، لكن سيتعين علينا الانتظار لمعرفة ما إذا كانت الدراسات المستقبلية ستجد أي ثغرات أمنية.

شهادات رقمية

يمكن لأي شخص بسهولة جعل زوج رئيسي ، حتى المهاجم. فما الذي يمنع أي شخص من صنع مجموعة من المفاتيح والتظاهر بأنه الرئيس ، أو التظاهر كأي شخص آخر?

حسنًا ، لا يوجد شيء يمنع أي شخص من الادعاء بأنه شخص آخر ، ولكن يوجد نظام يسمح للآخرين بالتحقق مما إذا كان الشخص هو حقًا هو الذي يزعم أم لا. يطلق عليه البنية التحتية للمفتاح العام (PKI), وهذا ينطوي الشهادات الرقمية التي تربط المفتاح العام للفرد أو الكيان بهويته الحقيقية. هذه الشهادات موقعة من قِبل آخرين للإشارة إلى مدى موثوقية الشهادة.

يمكنك مقارنة العملية باستخدام كتاب العدل للتحقق من المستندات. إذا كان لدى شخص ما نسخة من شهادة الميلاد ، فقد تكون متشككًا فيما إذا كانت شرعية أم لا. إذا تم توقيع شهادة الميلاد نفسها وختمها من قبل كاتب عدل ، فمن الأرجح أن تصدق أنها نسخة حقيقية.

لماذا ا?

لأن التوقيع والطوابع يُظهران أن كيانًا عامًا موثوقًا به قد شاهد الفرد وشهادة الميلاد الأصلية الخاصة به ، ثم تحقق من أن النسخة في الواقع شرعية. يقوم كاتب العدل بالتحقق من صحة نسخة شهادة الميلاد ويضع سمعتها خلفها بتوقيعهم وختمهم.

يتم نقل الثقة التي نمتلكها لكاتب العدل إلى نسخة من شهادة الميلاد ، مما يسمح لنا أن نثق بها أكثر من شهادة لم يتم توثيقها.

هناك نوعان رئيسيان من الشهادات ، جالسلطات المختصة (CAs) وشبكة الثقة.

سلطات الشهادة

سلطات الشهادة هي تقوم المنظمات الموثوقة التي تقوم بالتحقق من الأفراد أو الكيانات للتحقق مما إذا كانوا المالك الشرعي للمفتاح العمومي. إذا كشفت الشيكات أن الفرد هو المالك الحقيقي ، فستوقع سلطة الشهادة الشهادة بمفتاحها الخاص ، مما يدل على أنها أكملت الشيك وتعتقد أن المفتاح الفردي والمفتاح العمومي مرتبطان بشكل قانوني.

طالما نثق بمرجع الشهادة وعملية التحقق من المفتاح ، فيمكننا الوثوق بشهادة تم توقيعها بواسطتها, وبالتالي فإن المفتاح العمومي يمثل هذا الشخص حقًا.

اعتمادًا على نوع الشهادة وتطبيقها ، يمكن أن يكون للمستويات المختلفة عمليات تحقق مختلفة ، وبالتالي تمثل درجة أعلى أو أقل من الثقة.

شبكة الثقة

شبكة الثقة تعمل تحت فرضية مماثلة ، باستثناء رلا توجد هيئات مركزية مثل المراجع المصدقة التي تقوم بعملية التحقق وتوقيع الشهادات.

بدلاً من ذلك ، تعتمد شبكة الثقة على الأفراد الآخرين للتوقيع على الشهادات ، وإثبات سمعتهم على الرابط بين الفرد والمفتاح العمومي. يستخدم هذا النظام في الغالب مع PGP ، حيث يمكن للمستخدمين إجراء شهاداتهم بسهولة.

يعمل مثل هذا:

دعنا نقول أن لديك صديقين يريدون توقيع شهاداتهما لإثبات أنهما المالكان الشرعيان للمفاتيح العامة لكل منهما. أنت تعرف هؤلاء الأشخاص جيدًا ، وهم يعرضون عليك بطاقات الهوية الحكومية الخاصة بهم ، مما يجعلك متأكدًا تمامًا من أنهم يقولون إنهم ، وبالتالي هم المالكون الحقيقيون للمفاتيح العامة التي يدعونها..

نظرًا لأنك تعلم أنها المالك الشرعي للمفاتيح العامة الخاصة بها ، فأنت سعيد باستخدام المفتاح الخاص لتوقيع شهاداتهم وإثبات سمعتك عليها والقول بشكل أساسي “نعم ، لقد قمت بالتحقق من هويات هؤلاء الأفراد وهم الذين يزعمون أنهم “. يمكن لهذين الصديقين فعل الشيء نفسه لك.

دعنا نقول أن لكل صديق من أصدقائك صديقين آخرين يريدان توقيع شهاداتهما. إذا وقع صديقانك على هذه الشهادات الأخرى ، فيمكنك استخدام الثقة التي لديك في أصدقائك لقبول أن هؤلاء الأشخاص الآخرين هم حقًا من يقولون أنهم كذلك.

يمكن لأصدقائك بعد ذلك التوقيع على شهادات الأشخاص الذين يثقون بهم وما إلى ذلك ، وبناء شبكة كبيرة من الأفراد الموثوق بهم. بمجرد أن تصبح هذه الشبكات كبيرة بما يكفي وتصبح مترابطة مع شبكات أخرى, يمكن استخدامها كوسيلة للثقة بأي شخص آخر في الشبكة.

كلما زاد عدد التواقيع على الشهادة ، خاصة إذا كانت توقيعات من أفراد موثوق بهم بدرجة عالية, كلما زادت ثقتك في الشهادة الرقمية لشخص ما والرابط بين المفتاح العمومي وهويته.

غالبًا ما يعقد مستخدمو PGP حفلات توقيع رئيسية حيث يتجمع الناس من أجل التحقق من هوياتهم وتوقيع شهاداتهم الرقمية. تساعد هذه التجمعات على جلب أشخاص جدد إلى الشبكة.

على الرغم من أنها تأتي مع بعض التعقيدات ، إلا أن ميزة شبكة نظام الثقة هي أنه لا توجد هيئة مركزية يمكن أن تتلف.

هي التوقيعات الرقمية آمنة?

بشكل عام, التواقيع الرقمية آمنة ما لم يتم اختراق المفتاح الخاص للشخص الموقّع. إذا أبلغ المالك شخصًا آخر أو ترك المفتاح الخاص مكتوبًا أو سُرق بطريقة أخرى ، فمن الممكن للمهاجمين توقيع الرسائل رقميًا كما لو كانوا المالك.

يمكن أن يؤدي هذا إلى قيام المهاجم بانتحال شخصية ضحيته أو العبث ببياناته. هذه مشكلة أمنية ضخمة ، ويجب على أي شخص يشك في أن مفتاحه قد تم اختراقه إلغاء شهادةه الرقمية التي تربطهم بالمفتاح العام ، وإصدار شهادة جديدة.

هناك بعض المحاذير الأخرى عندما يتعلق الأمر بأمان التوقيعات الرقمية. يجب استخدام خوارزمية توقيع رقمي مناسبة ، كما يجب تنفيذها بشكل صحيح. إلى جانب ذلك ، يجب أيضًا أن تكون هناك طريقة لربط المفتاح العمومي بمالكه ، عادةً من خلال الشهادات الرقمية.

طالما تم استيفاء هذه المتطلبات ، فأنت تتبع أفضل الممارسات الصناعية ، ولم يتم اختراق المفتاح الخاص بك التواقيع الرقمية هي وسيلة ممتازة لتوفير الأصالة والنزاهة وعدم التنصل من البيانات.

البيانات المهيكلة بواسطة كاي Stachowiak مرخصة بموجب CC0