ما هو تبادل مفتاح Diffie-Hellman وكيف يعمل؟

كان تبادل مفتاح Diffie-Hellman واحدة من أهم التطورات في تشفير المفتاح العام ولا يزال يتم تنفيذه بشكل متكرر في مجموعة من البروتوكولات الأمنية المختلفة اليوم.

يسمح للطرفين الذين لم يلتقوا سابقًا بإنشاء المفتاح الذي يمكنهم استخدامه لتأمين اتصالاتهم بشكل آمن. في هذه المقالة ، سنشرح ما يتم استخدامه ، وكيف يعمل على أساس تدريجي ، وأشكاله المختلفة ، بالإضافة إلى اعتبارات الأمان التي يجب مراعاتها من أجل تنفيذها بأمان.

ما هو تبادل مفتاح Diffie-Hellman?

وكان مفتاح ديفي هيلمان الصرف أول طريقة تستخدم على نطاق واسع لتطوير بأمان وتبادل المفاتيح عبر قناة غير آمنة.

قد لا يبدو الأمر مثيرًا للغاية أو رائدًا في الشروط المذكورة أعلاه ، لذلك دعونا نعطي مثالًا يوضح لماذا كان تبادل مفتاح Diffie-Hellman بمثابة معلم هام في عالم التشفير ، ولماذا لا يزال يستخدم بشكل متكرر حتى اليوم.

دعنا نقول أنك جاسوس سري للغاية وأنك بحاجة إلى إرسال بعض المعلومات المهمة إلى مقرك الرئيسي. كيف تمنع اعدائك من الحصول على ahold للرسالة?

الحل الأكثر شيوعًا هو تشفير الرسالة برمز. أسهل طريقة هي إجراء اختبار مسبق لأي نوع من التعليمات البرمجية والمفتاح الذي تخطط لاستخدامه مسبقًا ، أو للقيام بذلك عبر قناة اتصال آمنة.

دعنا نقول أنك جاسوس سيئ للغاية ، وأنك ومقرك يقرران استخدام تشفير تحويل ضعيف لترميز رسائلك. في هذا الرمز ، يصبح كل “a” “b” ، وكل “b” يصبح “c” ، وكل “c” يصبح “d” ، وهكذا ، على طول الطريق حتى يصبح “z” “a”.

تحت رمز التبديل هذا ، تصبح الرسالة “دعنا نتناول العشاء” “Mfu’t hfu ejoofs”. لحسن الحظ ، في وضعنا الافتراضي ، فإن خصومك غير كفؤين تمامًا كما أنهم غير قادرين على كسر هذه الشفرة البسيطة ، والتي تمنعهم من الوصول إلى محتويات الرسالة..

ولكن ماذا يحدث إذا لم تتمكن من ترتيب رمز مع المستلم مسبقًا?

دعنا نقول أنك تريد التواصل مع جاسوس من دولة متحالفة لم تقابله من قبل. ليس لديك قناة آمنة يمكنك التحدث إليها. إذا لم تقم بتشفير رسالتك ، فسيتمكن أي خصم يعترض من قراءة المحتويات. إذا قمت بتشفيرها دون إخبار الحليف بالرمز ، فلن يتمكن العدو من قراءته ، لكن لن يقوم الحليف أيضًا.

كانت هذه القضية واحدة من أكبر الألغاز في التشفير حتى سبعينيات القرن الماضي:

كيف يمكنك تبادل المعلومات بشكل آمن مع شخص ما إذا لم تتح لك الفرصة لمشاركة المفتاح في وقت مبكر?

كان تبادل مفاتيح Diffie-Hellman أول آلية مستخدمة بشكل عام لحل هذه المشكلة. تسمح الخوارزمية لأولئك الذين لم يلتقوا من قبل بإنشاء مفتاح مشترك بأمان ، حتى عبر قناة غير آمنة قد يراقبها الخصوم.

تاريخ تبادل مفتاح Diffie-Hellman

يتتبع تبادل مفتاح Diffie-Hellman جذوره إلى السبعينيات. على الرغم من أن مجال التشفير قد تطور بشكل كبير خلال أوائل القرن العشرين ، فقد ركزت هذه التطورات بشكل رئيسي في مجال تشفير المفتاح المتماثل.

لم يكن حتى عام 1976 أن ظهرت خوارزميات المفتاح العام في المجال العام ، عندما نشر ويتفيلد ديفي ومارتن هيلمان ورقتهما, اتجاهات جديدة في التشفير. أوجز التعاون الآليات الكامنة وراء نظام جديد ، والذي أصبح يعرف باسم ديفي هيلمان تبادل المفاتيح.

استلهم العمل جزئياً من التطورات السابقة التي قام بها رالف ميركل. ما يسمى الألغاز ميركل إشراك طرف واحد في إنشاء وإرسال عدد من الألغاز المشفرة إلى الطرف الآخر. هذه الألغاز ستحتاج إلى كمية معتدلة من الموارد الحسابية لحلها.

سيختار المتلقي بشكل عشوائي لغزًا واحدًا لحله ثم يبذل الجهد اللازم لإكماله. بمجرد حل اللغز ، يتم الكشف عن المعرف ومفتاح الجلسة للمستلم. يقوم المستلم بعد ذلك بإرسال المعرف مرة أخرى إلى المرسل الأصلي ، مما يتيح للمرسل معرفة اللغز الذي تم حله.

نظرًا لأن المرسل الأصلي أنشأ الألغاز ، فإن المعرف يتيح لهم معرفة مفتاح الجلسة الذي اكتشفه المستلم ، ويمكن للطرفين استخدام هذا المفتاح للتواصل بشكل أكثر أمانًا. إذا كان المهاجم يستمع إلى التفاعل ، فسيتمكن من الوصول إلى جميع الألغاز ، بالإضافة إلى المعرف الذي يرسله المستلم مرة أخرى إلى المرسل الأصلي.

المعرف لا يخبر المهاجم عن مفتاح الجلسة الذي يتم استخدامه ، لذلك فإن أفضل طريقة لفك تشفير المعلومات هي حل جميع الألغاز للكشف عن مفتاح الجلسة الصحيح. نظرًا لأن المهاجم سيضطر إلى حل نصف الألغاز في المتوسط ​​، فسيصبح الأمر أكثر صعوبة بالنسبة لهم للكشف عن المفتاح مما هو عليه بالنسبة للمستلم.

يوفر هذا النهج مزيدًا من الأمان ، لكنه بعيد عن الحل الأمثل. أخذ تبادل مفاتيح Diffie-Hellman بعض هذه الأفكار وجعلها أكثر تعقيدًا من أجل إنشاء طريقة آمنة لتشفير المفتاح العام.

على الرغم من أنه أصبح معروفًا بتبادل مفتاح Diffie-Hellman ، فقد اقترح Martin Hellman تسمية الخوارزمية بتبادل مفتاح Diffie-Hellman-Merkle بدلاً من ذلك ، لتعكس العمل الذي وضعه Ralph Merkle نحو تشفير المفتاح العام.

كان يُعتقد بشكل عام أن Merkle و Hellman و Diffie كانوا أول من قام بتطوير تشفير المفتاح العام حتى عام 1997 ، عندما قامت الحكومة البريطانية بإلغاء السرية عن العمل المنجز في أوائل السبعينيات جيمس إليس ، كليفورد كوكس ومالكولم ويليامسون.

اتضح أن الثلاثي توصل إلى أول نظام تشفير للمفتاح العام بين عامي 1969 و 1973 ، ولكن تم تصنيف عملهم لمدة عقدين. وقد أجريت تحت قيادة الاتصالات الحكومية (GCHQ) ، وهي وكالة استخبارات بريطانية.

كان اكتشافهم في الواقع خوارزمية RSA ، لذلك كان Diffie و Hellman و Merkle لا يزالون أول من طور تبادل مفاتيح Diffie-Hellman ، لكن لم يعد أول مخترعين لتشفير المفتاح العام.

أين يتم استخدام المفتاح Diffie-Hellman?

الغرض الرئيسي من تبادل مفتاح Diffie-Hellman هو تطوير آمن الأسرار المشتركة التي يمكن استخدامها لاشتقاق المفاتيح. يمكن عندئذٍ استخدام هذه المفاتيح مع خوارزميات مفتاح متماثل لنقل المعلومات بطريقة محمية. تميل الخوارزميات المتماثلة إلى تشفير الجزء الأكبر من البيانات لأنها أكثر كفاءة من خوارزميات المفتاح العام.

من الناحية الفنية ، يمكن استخدام تبادل مفاتيح Diffie-Hellman لإنشاء مفاتيح عامة وخاصة. ومع ذلك ، في الممارسة العملية ، تميل RSA لاستخدامها بدلاً من ذلك. هذا لأن خوارزمية RSA قادرة أيضًا على توقيع شهادات المفتاح العام ، في حين أن تبادل مفاتيح Diffie-Hellman ليس كذلك.

تعتمد خوارزمية ElGamal ، التي كانت تستخدم بكثرة في PGP ، على تبادل مفتاح Diffie-Hellman ، لذلك فإن أي بروتوكول يستخدمه يعمل بشكل فعال على تنفيذ نوع من Diffie-Hellman.

باعتبارها واحدة من أكثر الطرق شيوعًا لتوزيع المفاتيح بأمان ، فإن تبادل مفاتيح Diffie-Hellman هو يتم تطبيقه بشكل متكرر في بروتوكولات الأمان مثل TLS و IPsec و SSH و PGP وغيرها الكثير. هذا يجعلها جزءًا لا يتجزأ من اتصالاتنا الآمنة.

كجزء من هذه البروتوكولات ، غالبًا ما يستخدم تبادل مفاتيح Diffie-Hellman للمساعدة في تأمين اتصالك بموقع ويب ، وللوصول عن بعد إلى كمبيوتر آخر ، ولإرسال رسائل بريد إلكتروني مشفرة

كيف يعمل تبادل مفتاح Diffie-Hellman؟?

يعد تبادل مفاتيح Diffie-Hellman معقدًا ، وقد يكون من الصعب أن تتعرف على كيفية عمله. ويستخدم أعداد كبيرة جدا والكثير من الرياضيات, شيء لا يزال الكثير منا يخاف من تلك الدروس الثانوية الطويلة والمملة.

لجعل الأمور أسهل قليلا لفهم, سنبدأ بشرح تبادل مفتاح Diffie-Hellman مع القياس. بمجرد أن يكون لديك فكرة كبيرة عن كيفية عملها ، سننتقل إلى وصف أكثر تقنية للعمليات الأساسية.

أفضل تشبيه لمخطط ديفي هيلمان هو التفكير فيه شخصين خلط الطلاء. دعنا نستخدم معيار التشفير ونقول أن أسمائهم أليس وبوب. كلاهما يتفق على لون عشوائي لتبدأ. دعنا نقول أنهم يرسلون رسالة و اتخاذ قرار بشأن اللون الأصفر المشترك, تماما كما في الرسم البياني أدناه:

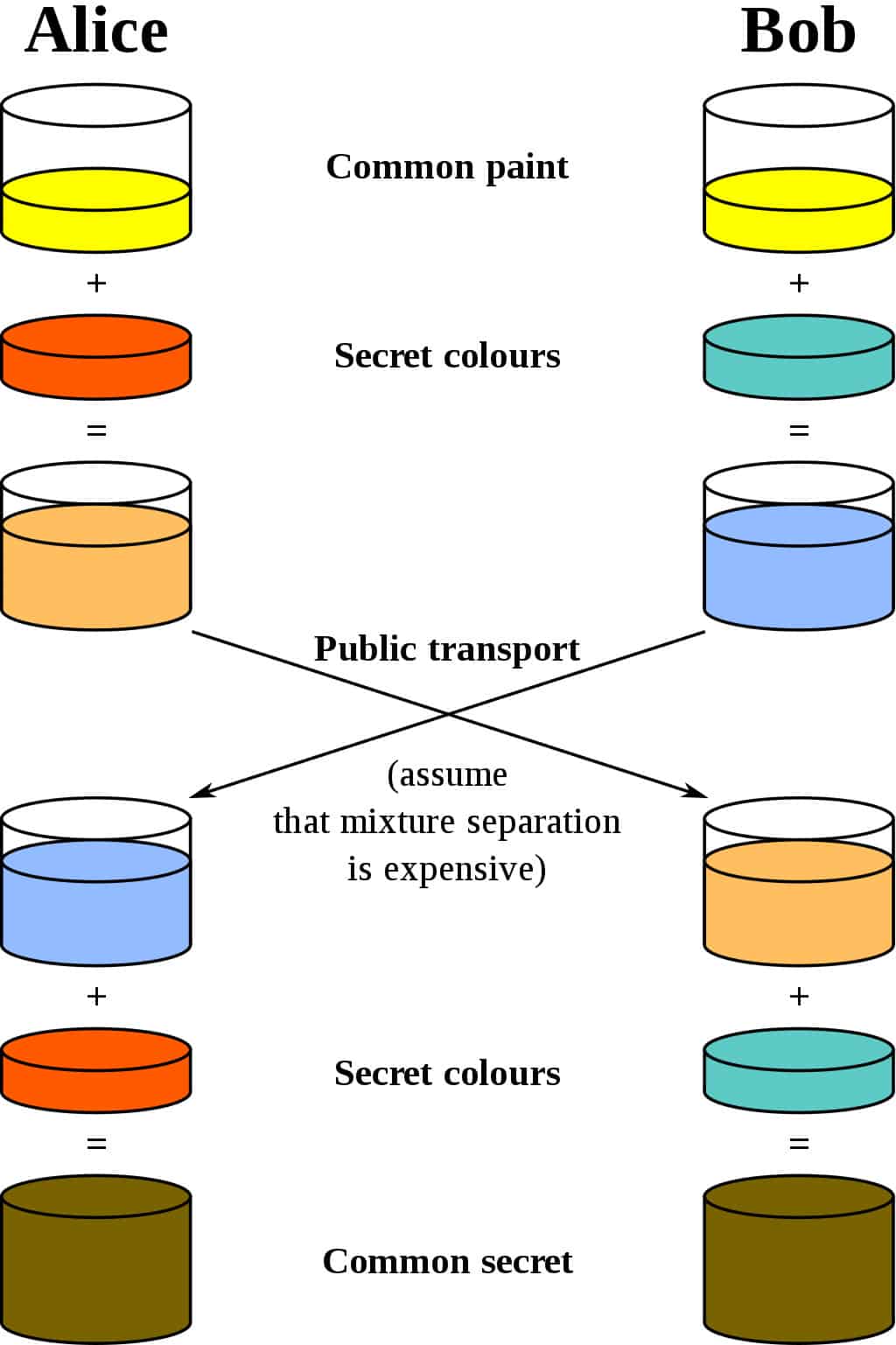
حد ذاته لونه السري. إنهم لا يخبرون الطرف الآخر اختيارهم. دعنا نقول أن أليس تختار أحمر, بينما يختار بوب أ الأزرق المخضر قليلا.

والخطوة التالية هي أن يقوم كل من أليس وبوب بمزج اللون السري بينهما (اللون الأحمر بالنسبة إلى أليس والأزرق المخضر لبوب) باللون الأصفر الذي اتفقا عليهما بشكل متبادل. وفقا للرسم البياني ، أليس ينتهي مع مزيج البرتقال, في حين أن نتيجة بوب هي الأزرق أعمق.

بمجرد الانتهاء من الخلط ، يرسلون النتيجة إلى الطرف الآخر. أليس تستقبل اللون الأزرق الأعمق, في حين يتم إرسال بوب الطلاء البرتقالي اللون.

بمجرد حصولهم على النتيجة المختلطة من شريكهم ، يضيفون لونهم السري إليها. تأخذ أليس اللون الأزرق الأعمق وتضيف الطلاء الأحمر السري, في حين يضيف بوب سرته باللون الأزرق المخضر إلى المزيج البرتقالي الذي تلقاه للتو.

النتيجة? كلاهما يخرج بنفس اللون, وهو في هذه الحالة هو اللون البني مثير للاشمئزاز. قد لا يكون هذا النوع من الألوان الذي تريد أن ترسم غرفة المعيشة الخاصة بك ، لكنه مع ذلك لون مشترك. يشار إلى هذا اللون المشترك باسم سر مشترك.

الجزء الحاسم من تبادل مفاتيح Diffie-Hellman هو أن ينتهي كلا الطرفين بالنتيجة نفسها ، دون الحاجة إلى إرسال السر المشترك بالكامل عبر قناة الاتصال. إن اختيار لون شائع ، وألوانه السرية الخاصة ، وتبادل المزيج ثم إضافة لونه مرة أخرى ، يمنح الطرفين وسيلة للوصول إلى نفس السر المشترك دون الحاجة إلى إرسال أي شيء على الإطلاق..

إذا كان المهاجم يستمع إلى البورصة ، فكل ما يمكنهم الوصول إليه هو اللون الأصفر الشائع الذي يبدأ به أليس وبوب ، وكذلك الألوان المختلطة التي يتم تبادلها. لأن هذا يتم حقا بأعداد هائلة بدلا من الطلاء, لا تعد هذه المعلومات كافية للاعتداء على أيٍّ من الألوان السرية الأولية أو السر المشترك (من الناحية الفنية ، من الممكن حساب السر المشترك من هذه المعلومات ، ولكن في التنفيذ الآمن لتبادل مفتاح Diffie-Hellman ، سيستغرق الأمر وقتًا طويلاً وموارد حسابية للقيام بذلك).

هذا الهيكل لتبادل مفتاح Diffie-Hellman هو ما يجعله مفيدًا للغاية. يسمح للطرفين بالاتصال عبر اتصال يحتمل أن يكون خطيرًا ويظلان يكتشفان سرًا مشتركًا يمكنهما استخدامه لإنشاء مفاتيح تشفير لاتصالاتهما المستقبلية. لا يهم ما إذا كان أي مهاجمين يستمعون إليه ، لأن السر المشترك الكامل لا يتم إرساله عبر الاتصال.

التفاصيل الفنية لتبادل مفتاح Diffie-Hellman

الوقت لبعض الرياضيات …

لا تقلق ، سوف نتباطأ ونحاول جعل العملية برمتها سهلة الفهم قدر الإمكان. يتبع فرضية مشابهة للتشبيه الموضح أعلاه ، ولكن بدلاً من خلط الألوان وإرسالها, يقوم نظام Diffie-Hellman بإجراء حسابات استنادًا إلى أعداد أولية كبيرة جدًا ، ثم يرسلها عبرها.

لضمان الأمن ، فمن المستحسن أن رئيس الوزراء (ص) يبلغ طوله 2048 بت على الأقل, وهو المكافئ الثنائي لعدد عشري حول هذا الحجم:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

لمنع رأس أي شخص من الانفجار ، سنقوم بتنفيذ هذا التفسير بأعداد أقل بكثير. كن حذرا ان سيكون تبادل مفاتيح Diffie-Hellman غير آمن إذا استخدم أرقامًا صغيرة مثل تلك الموجودة في مثالنا. نحن نستخدم هذه الأرقام الصغيرة فقط لإظهار المفهوم بطريقة أبسط.

في أبسط أشكال تبادل مفتاح Diffie-Hellman, يبدأ أليس وبوب بتحديد عدد متبادل بينهما, على عكس الطلاء المشترك واحد في المثال أعلاه. وهذه هي معامل (ص) والقاعدة (ز).

في الاستخدام العملي, المعامل (ع) عدد أولي كبير جدًا, في حين القاعدة (ز) صغير نسبيا لتبسيط العمليات الحسابية. القاعدة (ز) مشتق من مجموعة دورية (G) التي يتم إنشاؤها عادة قبل وقت طويل من اتخاذ الخطوات الأخرى.

على سبيل المثال لدينا ، دعنا نقول أن معامل (ص) يكون 17, بينما القاعدة (ز) يكون 4.

بمجرد اتخاذ قرار متبادل بشأن هذه الأرقام ، تستقر أليس على رقم سري (أ) لنفسها ، بينما يختار بوب رقمه السري الخاص (ب). دعنا نقول أنهم يختارون:

أ = 3

ب = 6

تقوم أليس بعد ذلك بالحساب التالي لمنحها الرقم الذي سترسله إلى بوب:

A = ga mod p

في الحساب أعلاه, عصري يدل على عملية modulo. هذه هي الحسابات الأساسية لمعرفة الباقي بعد تقسيم الجانب الأيسر على اليمين. كمثال:

15 وزارة الدفاع 4 = 3

إذا فهمت كيف تعمل عمليات المودولو ، يمكنك القيام بها بنفسك في الحسابات التالية ، وإلا يمكنك استخدام آلة حاسبة على الإنترنت.

لذلك دعونا نضع أرقامنا في الصيغة:

A = 43 وزارة الدفاع 17

A = 64 وزارة الدفاع 17

A = 13

عندما نفعل نفس الشيء مع Bob ، نحصل على:

ب = 46 وزارة الدفاع 17

ب = 4096 وزارة الدفاع 17

ب = 16

أليس ثم ترسل النتيجة لها (أ) إلى Bob ، بينما يرسل Bob رقمه (بإلى أليس. أليس تحسب السر المشترك (س) باستخدام الرقم الذي تلقته من Bob (ب) ورقمها السري (أ) ، باستخدام الصيغة التالية:

س = با وزارة الدفاع ص

س = 163 وزارة الدفاع 17

س = 4096 وزارة الدفاع 17

س = 16

يقوم بوب بعد ذلك بنفس الحساب ، لكن بالعدد الذي أرسله إليه أليس (أ) ، وكذلك رقمه السري الخاص (ب):

س = أب عصري ص

س = 136 وزارة الدفاع 17

س = 4826809 وزارة الدفاع 17

ق = 16

كما ترون ، انتهى كلا الطرفين بنفس النتيجة لـ س, 16. هذا هو السر المشترك ، الذي يعرفه أليس وبوب فقط. يمكنهم بعد ذلك استخدام هذا لإعداد مفتاح للتشفير المتماثل ، مما يتيح لهم إرسال المعلومات بأمان فيما بينهم بطريقة يمكنهم فقط الوصول إليها.

لاحظ أنه على الرغم من ب و س هي نفسها في المثال أعلاه ، هذه مجرد صدفة تعتمد على الأرقام الصغيرة التي تم اختيارها لهذا الرسم التوضيحي. عادةً ، لن تكون هذه القيم هي نفسها في التنفيذ الفعلي لتبادل المفاتيح Diffie-Hellman.

على الرغم من أن الكثير من البيانات أعلاه يتم إرسالها عبر القناة بنص واضح (ع ، ز ، أ و ب) ويمكن قراءتها من قبل المهاجمين المحتملين ، السر المشترك (س) لا ينتقل أبدا. لن يكون من العملي بالنسبة للمهاجم حساب السر المشترك (س) أو أي من الأرقام السرية (أ و ب) من المعلومات التي يتم إرسالها في نص واضح.

بالطبع ، هذا يفترض أن تبادل مفاتيح Diffie-Hellman قد تم تنفيذه بشكل صحيح وأنه يتم استخدام أعداد كبيرة بما فيه الكفاية. طالما تم الالتزام بهذه الأحكام ، يعتبر تبادل مفاتيح Diffie-Hellman طريقة آمنة لإنشاء سر مشترك يمكن استخدامه لتأمين الاتصالات المستقبلية.

إنشاء مفتاح مشترك بين أطراف متعددة

يمكن أيضًا استخدام تبادل مفاتيح Diffie-Hellman لإعداد مفتاح مشترك مع عدد أكبر من المشاركين. إنه يعمل بنفس الطريقة ، باستثناء ما يلزم من جولات الحسابات الإضافية لكل طرف لإضافة رقمه السري وينتهي به الأمر مع نفس السر المشترك.

تمامًا كما هو الحال في الإصدار المكون من طرفين من تبادل مفاتيح Diffie-Hellman ، يتم إرسال بعض أجزاء المعلومات عبر قنوات غير آمنة ، لكن هذا لا يكفي لكي يتمكن المهاجم من حساب السر المشترك..

لماذا يعد تبادل مفتاح Diffie-Hellman آمنًا?

على المستوى الرياضي ، يعتمد تبادل مفاتيح Diffie-Hellman على الوظائف أحادية الاتجاه كأساس لأمانها. هذه هي العمليات الحسابية البسيطة التي يمكن القيام بها بطريقة واحدة ، ولكن يصعب حسابها في الاتجاه المعاكس.

وبشكل أكثر تحديدًا ، تعتمد على مشكلة Diffie-Hellman ، التي تفترض أنه من غير الممكن حسابها وفقًا للمعايير الصحيحة. زأب من القيم المنفصلة لل ز, زأ و زب. لا توجد حاليًا طريقة معروفة للعثور عليها بسهولة زأب من القيم الأخرى ، وهذا هو السبب في أن تبادل مفاتيح Diffie-Hellman يعتبر آمنًا ، على الرغم من حقيقة أن المهاجمين يمكنهم اعتراض القيم ص, ز, أ, و ب.

المصادقة & تبادل مفتاح Diffie-Hellman

في العالم الواقعي ، نادراً ما يستخدم تبادل مفاتيح Diffie-Hellman من تلقاء نفسه. السبب الرئيسي وراء ذلك هو ذلك لا يوفر أي مصادقة ، مما يجعل المستخدمين عرضة لهجمات man-in-the-middle.

يمكن أن تحدث هذه الهجمات عندما يتم تنفيذ تبادل مفاتيح Diffie-Hellman من تلقاء نفسه ، لأنه ليس لديها أي وسيلة للتحقق مما إذا كان الطرف الآخر في اتصال هو بالفعل من يقولون إنهم. بدون أي شكل من أشكال المصادقة, المستخدمين قد يكون في الواقع التواصل مع المهاجمين عندما يعتقدون أنهم يتواصلون مع طرف موثوق.

لهذا السبب ، يتم تطبيق تبادل مفاتيح Diffie-Hellman بشكل عام جنبًا إلى جنب مع بعض وسائل المصادقة. يتضمن هذا غالبًا استخدام الشهادات الرقمية وخوارزمية المفتاح العام ، مثل RSA ، للتحقق من هوية كل طرف.

اختلافات تبادل مفتاح Diffie-Hellman

يمكن تنفيذ تبادل مفاتيح Diffie-Hellman بعدد من الطرق المختلفة ، كما وفر الأساس لعدة خوارزميات أخرى. توفر بعض هذه التطبيقات إذنًا ، في حين أن البعض الآخر لديه العديد من ميزات التشفير مثل سرية التوجيه إلى الأمام.

اهليلجيه منحنى ديفي هيلمان

منحنى إهليلجي يستفيد Diffie-Hellman من البنية الجبرية للمنحنيات الإهليلجية للسماح للتطبيقات بتحقيق مستوى مماثل من الأمان مع حجم مفتاح أصغر. يوفر مفتاح منحنى إهليلجي 224 بت مستوى الأمان نفسه كمفتاح RSA 2048 بت. هذا يمكن أن يجعل التبادلات أكثر كفاءة ويقلل من متطلبات التخزين.

بصرف النظر عن طول المفتاح الأصغر وحقيقة أنه يعتمد على خصائص المنحنيات الإهليلجية ، فإن المنحنى الإهليلجي يعمل بطريقة مماثلة لتبادل المفاتيح القياسي في Diffie-Hellman.

TLS   

يمكن لـ TLS ، وهو بروتوكول يُستخدم لتأمين جزء كبير من الإنترنت ، استخدام تبادل Diffie-Hellman بثلاث طرق مختلفة: مجهول ، ثابت وسريع الزوال. في الممارسة العملية ، يجب تنفيذ الزميلة ديفي هيلمان فقط ، لأن الخيارات الأخرى لها مشاكل أمنية.

• مجهول ديفي هيلمان – لا يستخدم هذا الإصدار من تبادل مفاتيح Diffie-Hellman أي مصادقة ، مما يجعله عرضة للهجمات التي تتم في الوسط. لا ينبغي أن تستخدم أو تنفذ.
• ساكنة ديفي هيلمان – يستخدم Static Diffie-Hellman الشهادات لمصادقة الخادم. لا يصادق العميل بشكل افتراضي ، كما أنه لا يوفر سرية إلى الأمام.
• سريعة الزوال ديفي هيلمان – يعتبر هذا التطبيق الأكثر أمانًا لأنه يوفر سرية مثالية للأمام. يتم دمجها عمومًا مع خوارزمية مثل DSA أو RSA للمصادقة على أحد الطرفين أو كلاهما في الاتصال. يستخدم Ephemeral Diffie-Hellman أزواج مفاتيح مختلفة في كل مرة يتم فيها تشغيل البروتوكول. هذا يمنح الاتصال سرية تامة للأمام ، لأنه حتى لو تم اختراق أحد المفاتيح في المستقبل ، فلا يمكن استخدامه لفك تشفير جميع الرسائل السابقة.

الجمل

ElGamal عبارة عن خوارزمية للمفتاح العام مبنية على قمة تبادل مفاتيح Diffie-Hellman. مثل Diffie-Hellman ، فإنه لا يحتوي على أحكام للمصادقة بمفرده ، ويتم دمجه عمومًا مع آليات أخرى لهذا الغرض.

تم استخدام ElGamal بشكل أساسي في PGP و GNU Privacy Guard وأنظمة أخرى لأن منافستها الرئيسية ، RSA ، حصلت على براءة اختراع. انتهت صلاحية براءة اختراع RSA في عام 2000 ، مما سمح بتنفيذها بحرية بعد ذلك التاريخ. منذ ذلك الحين ، لم يتم تنفيذ الجمل بشكل متكرر.

STS

يعتمد بروتوكول المحطة إلى المحطة (STS) أيضًا على تبادل مفاتيح Diffie-Hellman. إنه مخطط اتفاق رئيسي آخر ، ومع ذلك فهو يوفر الحماية ضد هجمات الرجل في الوسط فضلاً عن السرية التامة للأمام.

يتطلب الأمر أن يكون لدى كلا الطرفين في الاتصال بالفعل زوج مفاتيح ، والذي يستخدم لمصادقة كل جانب. إذا كانت الأطراف غير معروفة بالفعل لبعضها البعض ، فيمكن استخدام الشهادات للتحقق من هويات الطرفين.

تبادل مفتاح Diffie-Hellman & RSA

كما ناقشنا في وقت سابق, غالبًا ما يتم تطبيق تبادل مفاتيح Diffie-Hellman إلى جانب RSA أو خوارزميات أخرى لتوفير مصادقة للاتصال. إذا كنت معتادًا على RSA ، فقد تتساءل لماذا يزعج أي شخص استخدام تبادل مفاتيح Diffie-Hellman أيضًا, لأن RSA تمكن الأطراف التي لم تلتق من قبل من التواصل بشكل آمن.

تسمح RSA لمستخدميها بتشفير الرسائل باستخدام المفتاح العمومي لمراسلهم ، بحيث يمكن فك تشفيرهم فقط عن طريق المفتاح الخاص المطابق. ومع ذلك ، في الممارسة العملية, لا يستخدم RSA لتشفير الاتصالات بالكامل – فهذا سيكون غير فعال للغاية.

بدلاً من ذلك ، غالبًا ما يتم استخدام RSA فقط كوسيلة لمصادقة كلا الطرفين. هل هذا مع الشهادات الرقمية لكل طرف ، والتي سيتم التحقق منها بواسطة سلطة الشهادة لإثبات أن صاحب الشهادة هو حقًا ما يقوله هؤلاء ، وأن المفتاح العمومي الموجود في الشهادة ينتمي إليهم بالفعل.

للمصادقة المتبادلة, سيوقع كل طرف رسالة باستخدام مفتاحه الخاص ثم يرسلها إلى شريك الاتصال. يمكن لكل مستلم بعد ذلك تحقق من هوية الطرف الآخر عن طريق التحقق من الرسائل الموقعة مقابل المفتاح العمومي في الشهادة الرقمية لشريك الاتصال (انظر المقالة المذكورة أعلاه على RSA لمزيد من التفاصيل حول كيفية عمل هذا ، لا سيما توقيع الرسائل الجزء).

الآن وقد تمت المصادقة على كلا الطرفين ، فمن الممكن تقنيًا الاستمرار في استخدام RSA لإرسال الرسائل المشفرة بأمان فيما بينهما ، ومع ذلك فقد ينتهي الأمر بعدم الكفاءة.

للتغلب على عدم الكفاءة هذا ، تستخدم العديد من بروتوكولات الأمان خوارزمية مثل تبادل مفتاح Diffie-Hellman للتوصل إلى سر شائع يمكن استخدامه لإنشاء مفتاح مشترك متماثل. ثم يتم استخدام هذا المفتاح المتماثل في خوارزمية مفتاح متماثل ، مثل AES ، لتشفير البيانات أن الطرفين يعتزمان إرسال بأمان بينهما.

قد يبدو الأمر عملية معقدة ومعقدة ، لكن الأمر ينتهي به الأمر إلى أن يكون أسرع وأقل طلبًا على الموارد عند مقارنته باستخدام خوارزمية مفتاح عمومي للتبادل بالكامل. هذا بسبب تشفير المفتاح المتماثل هو أوامر ذات حجم أكبر من تشفير المفتاح العمومي.

بالإضافة إلى أوجه القصور التي ذكرناها للتو ، هناك بعض الجوانب السلبية الأخرى التي قد تأتي من استخدام RSA فقط. تحتاج RSA إلى الحشو لجعلها آمنة, لذلك سوف تحتاج إلى تنفيذ خوارزمية إضافية بشكل مناسب بجانبها لجعلها آمنة.

RSA لا توفر السرية التامة للأمام, إما ، وهو عيب آخر عند مقارنتها بتبادل المفاتيح المؤقتة Diffie-Hellman. بشكل جماعي ، هذه الأسباب هي أنه في العديد من الحالات ، من الأفضل تطبيق RSA فقط مع تبادل مفاتيح Diffie-Hellman.

بدلاً من ذلك ، يمكن دمج تبادل مفاتيح Diffie-Hellman مع خوارزمية مثل Digital Signature Standard (DSS) لتوفير المصادقة وتبادل المفاتيح والسرية والتحقق من سلامة البيانات. في مثل هذه الحالة ، RSA ليست ضرورية لتأمين الاتصال.

مشكلات الأمان في تبادل مفتاح Diffie-Hellman

يعتمد أمان تبادل مفتاح Diffie-Hellman على كيفية تنفيذه ، وكذلك على الأرقام التي يتم اختياره لها. كما ذكرنا أعلاه ، لا يوجد لديه وسيلة لمصادقة الطرف الآخر بنفسه ، ولكن في الممارسة العملية يتم استخدام آليات أخرى لضمان أن الطرف الآخر في اتصال ما ليس دجالًا.

معلمات لاختيار العدد

إذا كان التنفيذ الفعلي لتبادل مفاتيح Diffie-Hellman يستخدم أرقامًا صغيرة مثل تلك الموجودة في مثالنا ، فستجعل عملية التبادل تافهة للمهاجم للتصدع. ولكن ليس حجم الأرقام هو المهم فقط – بل يجب أن تكون الأرقام عشوائية بشكل كافٍ. إذا كان مولد الأرقام العشوائية ينتج مخرجات يمكن التنبؤ بها ، فيمكن أن يقوض تمامًا أمان تبادل مفاتيح Diffie-Hellman.

الرقم ص يجب أن يكون 2048 بت لضمان الأمن. القاعدة, ز, يمكن أن يكون عدد صغير نسبيا مثل 2, لكنه يحتاج أن يأتي من أمر G التي لديها عامل أولي كبير

الهجوم Logjam

تم تصميم تبادل مفاتيح Diffie-Hellman على أساس مشكلة اللوغاريتم المنفصلة التي يصعب حلها. الآلية الأكثر فاعلية المعروفة لإيجاد الحل هي خوارزمية غربال حقل الرقم.

تم أخذ قدرات هذه الخوارزمية في الاعتبار عند تصميم تبادل مفاتيح Diffie-Hellman. بحلول عام 1992 ، كان من المعروف أن لمجموعة معينة, G, يمكن حساب ثلاث من الخطوات الأربع المشاركة في الخوارزمية مسبقًا. إذا تم حفظ هذا التقدم ، فيمكن حساب الخطوة الأخيرة في وقت قصير نسبيًا.

لم يكن هذا أمرًا مهمًا للغاية حتى تم إدراك أن جزءًا كبيرًا من حركة المرور على الإنترنت يستخدم نفس المجموعات التي تبلغ 1024 بت أو أصغر. في عام 2015 ، أجرى فريق أكاديمي العمليات الحسابية الخاصة برابط 512 بت الأكثر شيوعًا الذي يستخدمه تبادل مفاتيح Diffie-Hellman في TLS.

كانوا أيضًا قادرين على خفض مستوى 80٪ من خوادم TLS التي تدعم DHE-EXPORT ، بحيث يقبلون تبادل مفاتيح Diffie-Hellman من فئة 512 بت للاتصال. هذا يعني ذاك كل من هذه الخوادم عرضة لهجوم من خصم جيد الموارد.

ذهب الباحثون لاستقراء نتائجهم, تقدير أن دولة القومية يمكن كسر رئيس 1024 بت. من خلال كسر العرض الأول 1024 بت الأكثر استخدامًا ، قدر الفريق الأكاديمي أن الخصم يمكن أن يراقب 18٪ من مواقع HTTPS الأكثر شهرة والتي يبلغ عددها مليون موقع.

واستمروا في القول إن الإصدار الثاني سيمكن الخصم من فك تشفير اتصالات 66٪ من خوادم VPN و 26٪ من خوادم SSH. في وقت لاحق من التقرير ، اقترح الأكاديميون أن وكالة الأمن القومي قد يكون لديها بالفعل هذه القدرات.

“إن القراءة عن كثب لتسريبات وكالة الأمن القومي المنشورة توضح أن هجمات الوكالة على الشبكات الافتراضية الخاصة تتفق مع تحقيق مثل هذا الاستراحة”.

على الرغم من مشكلة عدم الحصانة هذه ، لا يزال تبادل مفاتيح Diffie-Hellman آمنًا إذا تم تنفيذه بشكل صحيح. طالما تم استخدام مفتاح 2048 بت ، فلن يعمل هجوم Logjam. المتصفحات المحدثة آمنة أيضًا من هذا الهجوم.

هل تبادل مفتاح Diffie-Hellman آمن?

على الرغم من أن تبادل مفاتيح Diffie-Hellman قد يبدو معقدًا ، إلا أنه جزء أساسي من تبادل البيانات بشكل آمن عبر الإنترنت. طالما تم تطبيقه جنبًا إلى جنب مع طريقة المصادقة المناسبة وتم اختيار الأرقام بشكل صحيح ، فإنه لا يعتبر عرضة للهجوم.

كان تبادل مفاتيح Diffie-Hellman طريقة مبتكرة لمساعدة طرفين مجهولين على التواصل بأمان عندما تم تطويره في السبعينيات. بينما نقوم الآن بتنفيذ إصدارات أحدث مع مفاتيح أكبر للحماية من التكنولوجيا الحديثة يبدو أن البروتوكول نفسه سيبقى آمنًا حتى وصول الحوسبة الكمومية والهجمات المتقدمة التي ستأتي معها.

تكنولوجيا الأعمال الأمن السيبراني بواسطة TheDigitalArtist مرخص بموجب CC0