ما هو تشفير 3DES وكيف يعمل DES؟

3DES هو تشفير تشفير مشتق من معيار تشفير البيانات الأصلي (DES). أصبح بارزًا في أواخر التسعينات ، لكنه تراجع منذ ذلك الحين بسبب ظهور خوارزميات أكثر أمانًا.

على الرغم من أنه سيتم إهماله في عام 2023 ، إلا أنه لا يزال مطبقًا في بعض الحالات. نظرًا لأنه يعتمد على واحدة من الخوارزميات المنشورة والمدروسة على نطاق واسع ، وهي DES ، لا يزال من المهم معرفة ماهية 3DES وكيف تعمل.

سوف يأخذك هذا الدليل في كل خطوة من خطوات عملية DES بالتفصيل ، ثم يغطي كيفية تعديل DES في 3DES لجعله أكثر أمانًا. كما أنه يتناول العديد من مشكلات الأمان وما إذا كان يجب عليك استخدام الخوارزمية أم لا.

ما هو 3DES?

على الرغم من أنه معروف رسميًا باسم خوارزمية تشفير البيانات ثلاثية الأبعاد (3DEA) ، إلا أنه يشار إليه عادةً باسم 3DES. وذلك لأن خوارزمية 3DES تستخدم تشفير البيانات المعيارية (DES) ثلاث مرات لتشفير بياناتها.

DES هي خوارزمية مفتاح متماثل تستند إلى شبكة Feistel. باعتباره تشفير مفتاح متماثل ، فإنه يستخدم نفس المفتاح لكل من عمليات التشفير وفك التشفير. تجعل شبكة Feistel هاتين العمليتين متشابهتين تمامًا تقريبًا ، مما ينتج عنه خوارزمية أكثر فعالية في التنفيذ.

يحتوي DES على 64 بت من الكتلة وحجم المفتاح ، ولكن في الممارسة العملية ، يمنح المفتاح فقط 56 بت من الأمان. تم تطوير 3DES كبديل أكثر أمانًا بسبب طول مفتاح DES الصغير. في 3DES ، يتم تشغيل خوارزمية DES خلال ثلاث مرات بثلاثة مفاتيح ، ومع ذلك تعتبر آمنة فقط إذا تم استخدام ثلاثة مفاتيح منفصلة.

استخدامات 3DES

بمجرد أن تصبح نقاط الضعف في DES العادية أكثر وضوحًا ، تم اعتماد 3DES في مجموعة واسعة من التطبيقات. كان واحدا من مخططات التشفير الأكثر استخداما قبل ظهور AES.

بعض الأمثلة على تطبيقاتها شملت أنظمة دفع Microsoft Office و Firefox و EMV. العديد من هذه المنصات لم تعد تستخدم 3DES بسبب وجود بدائل أفضل.

أصدر المعهد الوطني للمعايير والتكنولوجيا (NIST) مسودة اقتراح تقول إن جميع أشكال 3DES سيتم إهمالها حتى عام 2023 وسيتم رفضها اعتبارًا من عام 2024 فصاعدًا. على الرغم من أنها مجرد مسودة ، إلا أن الاقتراح يشير إلى نهاية حقبة ما ، وقد مضى وقت طويل على الانتقال إلى خوارزميات أخرى أكثر أمانًا.

تاريخ تشفير 3DES

نظرًا لأن 3DES مشتقة من DES ، فمن الأفضل تقديم المعيار السابق أولاً. في السبعينيات ، كان المكتب الوطني للمعايير (NBS – تمت إعادة تسميته منذ ذلك الحين NIST) يبحث عن خوارزمية يمكنه استخدامها كمعيار لتشفير المعلومات الحكومية الحساسة وغير المصنفة..

قبل المكتب الوطني للإحصاء مقترحات لمعيار يلائم متطلباته ، لكن لم يكن أي من المرشحين من الجولة الأصلية مناسبًا. ودعا المزيد من التقديمات ، وهذه المرة أرسلت IBM من خلال خوارزمية طورها فريقها. تم الحصول على التقديم من تشفير لوسيفر الذي صممه هورست فيستل.

في عام 1975 ، تم نشر خوارزمية IBM بواسطة NBS باعتبارها معيار تشفير البيانات المقترح. تمت دعوة الجمهور للتعليق على التصميم ، الذي اجتذب بعض الانتقادات.

ادعى مصممو التشفير البارزون مثل Whitfield Diffie و Martin Hellman ، مصممو تبادل المفاتيح Diffie-Hellman ، أن طول المفتاح قصير للغاية وأن مربعات S قد تغيرت من تصميمها الأولي.

في ذلك الوقت ، اعتقد الكثيرون في مجتمع التشفير أن وكالة الأمن القومي قد خربت المشروع وأضعفت الخوارزمية ، بحيث تكون الوكالة الوحيدة التي يمكنها كسر DES.

عندما تم التحقيق في ذلك من قبل لجنة الاستخبارات التابعة لمجلس الشيوخ الأمريكي ، تبين أن “وكالة الأمن القومي أقنعت شركة IBM بأن حجم المفتاح المنخفض كان كافياً ؛ ساعد بشكل غير مباشر في تطوير هياكل S-Box ؛ واعتمدت أن خوارزمية DES النهائية كانت ، على حد علمهم ، خالية من أي ضعف إحصائي أو رياضي. “

ومضى التقرير نفسه يقول إن “NSA لم تتلاعب بالتصميم بأي شكل من الأشكال”. وقد تم دعم هذا من قبل بعض موظفي IBM السابقين الذين ادعوا أن خوارزمية DES صُممت بالكامل بواسطة فريق IBM.

تزعم الوثائق التي رفعت عنها السرية في وكالة الأمن القومي أن الوكالة “عملت عن كثب مع آي بي إم لتقوية الخوارزمية ضد الجميع باستثناء هجمات القوة الغاشمة وتعزيز جداول الإحلال …”

تم تخفيف الشكوك حول العبث بـ NSA في التسعينات بمجرد اكتشاف تحليل الشفرة التفاضلي علنًا. عندما تم اختبار الصناديق S-malta كثيرا مع التقنية الجديدة ، وجد أنها أكثر مقاومة للهجوم مما لو تم اختيارها عشوائيا.

يشير هذا إلى أن فريق IBM قد علم بالفعل بالتحليل التفريقي للشفرات في السبعينيات ، مع ادعاء ستيفن ليفي بأن وكالة الأمن القومي طلبت منهم الحفاظ على سرية التقنية من أجل حماية الأمن القومي.

ذات مرة ، سخر الكاتب المشهور بروس شناير ، “لقد تطلب الأمر من المجتمع الأكاديمي عقدين من الزمن لمعرفة أن” تعديلات “ضمانات الأمن القومي قد حسنت بالفعل أمان DES.”

على الرغم من الأسئلة الأولية حول أمان الخوارزمية ومشاركة ضمانات الأمن السلبية ، فقد تمت الموافقة على خوارزمية IBM كمعيار لتشفير البيانات في عام 1976. تم نشره في عام 1977 وتم إعادة تأكيده كمعيار في الأعوام 1983 و 1988 و 1993.

عندما نُشر التحليل الخطي لأول مرة في عام 1994 ، بدأ في إثارة أسئلة حول أمان الخوارزمية. في عام 1997 ، أعلنت نيست أنها تبحث عن خوارزمية لتحل محل DES. تم تكثيف الحاجة إلى خوارزمية جديدة مع تطور التكنولوجيا وزيادة الهجمات المحتملة.

أظهرت محاولات التكسير المختلفة أنه كان من الصعب كسر الخوارزمية أقل مما كان يعتقد سابقًا. في عام 1998 ، استطاعت الموزعة.net أن تكسر DES مدة 39 يومًا.

بحلول بداية عام 1999 ، كانت مؤسسة Deep Crack التابعة لمؤسسة Electronic Frontier Foundation قد خفضت الوقت إلى ما يزيد قليلاً عن 22 ساعة. هذا يدل على نهاية DES ، لأن الهجوم من هذا القبيل كان الآن في متناول خصوم جيد الموارد.

كانت القضية الرئيسية هي المساحة الرئيسية الصغيرة ، وكانت هناك حاجة ماسة لخوارزمية جديدة. كانت هذه مشكلة ، لأن الأمر سيستغرق عدة سنوات حتى يستقر نظام NIST على الخوارزمية التي أصبحت معيار الاستبدال ، معيار التشفير المتقدم (AES).

أثناء تحديد تشفير AES ، تم اقتراح 3DES كتدبير مؤقت. يتضمن تشغيل خوارزمية DES ثلاث مرات ، مع ثلاثة مفاتيح منفصلة. في عام 1999 ، تم التأكيد من جديد على DES ، ولكن مع 3DES كخوارزمية مثالية. تم السماح Normal DES فقط في التطبيقات القديمة.

أصبح 3DES خوارزمية تشفير واسعة النطاق ، على الرغم من أن الاستخدام الكثيف للموارد والقيود الأمنية أدت إلى استبداله AES في معظم حالات الاستخدام.

فهم خوارزمية DES

قبل أن نتحدث عن تفاصيل 3DES ، من المهم فهم خوارزمية DES المستمدة منها. لذلك دعونا نبدأ في البداية.

نحن نستخدم التشفير لتحويل بيانات النص العادي إلى نص مشفر ، وهي معلومات لا يمكن للمهاجمين الوصول إليها (طالما أننا نستخدم الخوارزميات المناسبة).

خوارزميات التشفير هي صيغ رياضية معقدة بشكل أساسي. عندما يتعلق الأمر بتشفير شيء مثل “دعنا نذهب إلى الشاطئ” ، فإن الكثير من الناس يشعرون بالارتباك. بعد كل شيء ، كيف يمكنك تطبيق الرياضيات على أشياء مثل الحروف والحروف?

ترميز النص

الحقيقة هي أن أجهزة الكمبيوتر لا تتعامل بالأحرف والشخصيات. بدلاً من ذلك ، يعملون على نظام من 1s و 0s يُعرف باسم ثنائي. يُعرف كل 1 أو 0 بالقليل ، وتعرف مجموعة من ثمانية منهم بالبايت.

يمكنك إما البحث عنه يدويًا أو استخدام محول عبر الإنترنت لمعرفة ذلك بشكل ثنائي ، يصبح “Let to go to the beach”:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 0110001 01 0101000 01100011 01101000

كتل

عندما يتم تشفير البيانات ، يتم تقسيمها إلى كتل منفصلة للمعالجة. يحتوي DES على حجم كتلة 64 بت ، مما يعني بشكل أساسي أن كل كتلة تناسب مزيجًا من 64 منها والأصفار. سيكون أول كتلة لدينا (أول 64 رقمًا من الرقم الثنائي الموضح أعلاه):

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

سيكون الثاني لدينا:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

وسيكون لدينا كتلة النهائي:

01100010 01100101 01100001 01100011 01101000

حشوة

ربما لاحظت أن الكتلة الثالثة يبلغ طولها 40 بت فقط. قبل أن يتم تشفيره ، يجب أن يكون حجمه يصل إلى 64 بت. ويتم ذلك مع حشوة, الذي ينطوي على إضافة معلومات إضافية إلى كتلة من أجل إكماله يمكن القيام بذلك من خلال عدد من المخططات المختلفة ، كما يمكن أن يؤدي ذلك إلى جعل المعلومات المشفرة أكثر صعوبة للتصدع ، لكننا لن ندرك ذلك في هذه المقالة..

الجدول الزمني DES الرئيسية

تستخدم خوارزميات التشفير مفاتيح لإضافة البيانات التي ستغير النتيجة النهائية للعملية. إذا كانت DES تشتمل فقط على خطوات مثل التقليب و S-boxes (يتم شرح التقليب أدناه ، بينما تتم تغطية S-boxes في الاستبدال القسم) ، كل ما سيتعين على المهاجم القيام به هو الكشف عن تفاصيل الخوارزمية ، ثم قم بكل خطوة في الاتجاه المعاكس لكشف الرسالة الأولية.

نظرًا لأن معظم خوارزمياتنا معروفة على نطاق واسع ، فإن هذا لن يضيف كثيرًا من الأمان. بدلاً من ذلك ، تتم إضافة مفاتيح سرية لتغيير الإخراج بطريقة لا يمكن التنبؤ بها فقط من خلال معرفة الخوارزمية (طالما يتم استخدام خوارزمية معقدة بشكل كافٍ).

يبدأ DES بمفتاح واحد ، يُستخدم لإنشاء مفاتيح فرعية يتم تطبيقها في كل جولة. هذا مفتاح 64 بت ، وهو نفس حجم كتلنا. دعنا نقول مفتاحنا هو:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

الآن ، أدخل هذا المفتاح في الملف الثنائي ، وهو الطريقة التي يتم بها التعبير عن البيانات عندما تقوم أجهزة الكمبيوتر بمعالجتها. عندما يتعامل البشر مع المفاتيح ، سوف يظهرون عادة كمزيج من الشخصيات ، شيء مثل هذا:

kj329nf982bc9wn1

في DES ، تتمثل الخطوة الأولى لاشتقاق مفاتيحنا الدائرية في تبديل المفتاح (تحريكه) وفقًا للجدول التالي:

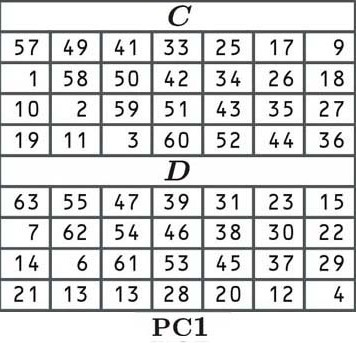
في التقليب ، يتم تبديل كل جزء من مفتاحنا الأصلي إلى موضع جديد كما هو موضح في الجدول. منذ الخلية في الزاوية اليسرى العليا (من C) يقول 57, سيكون الرقم الأول من مفتاحنا الثابت هو الرقم في الموضع السابع والخمسون من المربع القديم:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

الخلية الثانية تقول 49, مما يعني أن الرقم الثاني من مفتاحنا الجديد سيكون الرقم في الموضع 49 للكتلة القديمة:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

الخلية الثالثة تقول 41, لذلك نحن نبحث عن الرقم في الموضع 41:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

حتى الآن ، يتكون مفتاحنا من “110“.

يتم ترتيب بقية المفتاح بنفس الطريقة ، وفقًا لقيم الجدول. نتحرك من اليسار إلى اليمين ، وبمجرد أن نصل إلى نهاية صف ، نقفز إلى الصف التالي ، تمامًا مثل المعتاد. ذات مرة الجدول ج انتهى ، ونحن القفز إلى الجدول د لإكمال النصف الثاني من المفتاح.

لا توجد طريقة سهلة لتغيير مجموعتنا بالكامل وفقًا لجدول التقليب الأولي. يمكنك أن تفعل كل شيء يدويًا ، أو تكتب نصًا له (أو حتى تحصل على الحظ وتجد واحداً في أعماق الإنترنت) ، لكننا سنخدع ونصنعه:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

قد تشعر بالقلق من أننا نشكل بعض الأرقام في هذا الدليل ، ولكن الواقع هو أنه لا يهم حقًا. لا أحد يشفر البيانات يدويًا بعد الآن ، كل ذلك يتم عبر البرامج. الجانب الأكثر أهمية في هذا البرنامج التعليمي هو أن لديك فكرة واضحة عن المفاهيم التي نتعامل معها. الأرقام نفسها تخدم فقط لمساعدتك على تصور ما يجري.

ربما لاحظ بعض القراء أن الجدول (والآن مفتاحنا) ، يحتوي فقط على 56 بت بدلاً من 64. وهذا بسبب تخطي كل بتة الثامنة. هذا هو قطعة أثرية من الأيام القديمة للتكنولوجيا ، عندما كان من المهم أن يكون هناك بتات التحقق من التماثل ، والتي تتحقق مما إذا كان قد تم استلام المفتاح بشكل صحيح. تعني وحدات بت التحقق من التماثل هذه أنه في الممارسة العملية ، لا يحتوي DES إلا على أمان مفتاح 56 بت.

يعطينا الجدولان C و D مفتاحًا به نصفي 28 بت. في بعض الأحيان ، يشار إلى نصفي كـ C و D ، ولكن خلال هذه المقالة سوف نشير إليها باسم L و R ، لليسار واليمين. جانبنا الأيسر هو:

1100010 1010010 1010101 0101010

بينما حقنا هو:

1010000 1111001 0001011 1000111

تتمثل الخطوة التالية في تحويل المفتاح إما بمسافة واحدة أو اثنين إلى اليسار ، اعتمادًا على الجولة. يتم تحديد العدد الدقيق للمسافات وفقًا للجدول المحدد مسبقًا التالي:

رقم الجولة عدد التحولات اليسرى

1	1
2	1
3	2
4	2
5	2
6	2
7	2
8	2
9	1
10	2
11	2
12	2
13	2
14	2
15	2
16	1

لذلك دعونا نأخذ نصفينا الأيمن والأيسر:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

وتحول كلاهما موقف واحد إلى اليسار ، منذ الجولة الأولى لديه تحول 1 وفقًا للجدول (يتم نقل الرقم على الطرف الأيسر إلى النهاية اليمنى).

المفتاح الفرعي الجولة الأولى:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

في الجولة الثانية ، يقول الجدول أيضا 1, لذلك سيتم تغيير هذه النتيجة مرة أخرى عن طريق تحريك كل موقف رقم واحد إلى اليسار.

المرحلة الثانية المفتاح الفرعي:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

في الجولة الثالثة ، سيتم نقل الأرقام في مكانين إلى اليسار ، لأن الجدول يقول الآن 2.

المفتاح الفرعي الجولة الثالثة:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

في الجولات اللاحقة ، يتم نقل الأرقام إلى اليسار وفقًا للمسافات المحددة في الجدول ، مع تطبيق كل نوبة على نتيجة الجولة السابقة. في النهاية ، هذا يعطينا ستة عشر مفتاحًا فرعيًا مختلفًا ، واحد لكل جولة من عملية DES.

الخطوة التالية هي التقليب الآخر وفقًا لجدول PC2 الموضح أدناه:

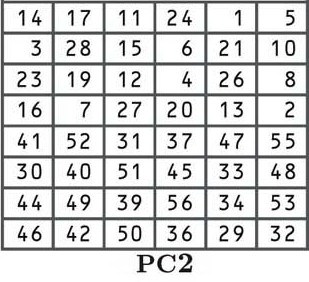
الآن ، يجب أن تكون على دراية بالتباديل ، لذلك لن ندخل في العملية بتعمق. إذا كنت تريد أن ترى كيف تعمل بمزيد من التفصيل ، فارجع إلى الشرح بالقرب من بداية هذا القسم. على الرغم من أن مواقع النقل مختلفة ، إلا أن العملية هي نفسها.

يتم الآن تبديل كل مفتاح من المفاتيح الـ 16 المشتقة في عملية النقل وفقًا للجدول ، مع نقل الرقم من الموضع الرابع عشر إلى المركز الأول ، والمفتاح 17 إلى الثاني ، والمركز 11 إلى المركز الثالث ، إلخ…

إذا نظرت عن كثب إلى الطاولة ، ستلاحظ أن هناك 48 بتًا فقط ، بدلاً من 56 بت كان لدينا سابقًا. تُعرف هذه العملية باسم التقليب بالضغط.

يمكنك أيضًا ملاحظة أن النصف العلوي من الجدول يحتوي على أرقام تتراوح بين 1 و 28 ، بينما يحتوي النصف السفلي على أرقام من 29 إلى 56. وهذا يبقي النصفين الأيسر والأيمن من مفاتيحنا الفرعية منفصلين ، ويشار إليه أدناه بمساحة أكبر في منتصف المفاتيح.

مرة أخرى ، سوف نقوم بخداع الأرقام. دعنا نقول أن هذه العملية برمتها أعطتنا المفاتيح الفرعية التالية:

الجولة الأولى:         010101 010101 101010 110100 101001 100101 101010 101010

الجولة الثانية:         011010 110101 101110 110010 010100 110010 111101 101101

الجولة الثالثة:     010100 100110 110110 101010 100110 011000 101011 011001

الجولة الرابعة:         011001 110101 011001 110101 000011 001011 010101 010101

الجولة الخامسة:         110101 001101 010101 010101 010011 001011 010111 100101

الجولة السادسة:           010111 110101 011001 111001 101001 100101 101010 101010

الجولة السابعة:     110101 111010 101110 101010 100110 010110 111011 001110

الجولة الثامنة:       011001 110101 010101 001001 010011 001011 010100 101010

الجولة التاسعة:         111011 011010 011110 100010 100010 010110 110011 110010

الجولة 10:             011010 010101 101110 101001 010010 010110 111000 101010

الجولة 11:             110101 001101 101110 101010 100101 100101 101010 001010

الجولة 12:             101001 100100 101001 101010 100110 011000 101011 011001

الجولة 13:             010010 010010 010101 010101 010110 110001 100101 101010

الجولة 14:             101001 100110 010101 011101 010001 001010 110010 111110

الجولة 15:             011001 011010 011001 110101 001001 011001 100101 101101

الجولة 16:             010010 100110 010101 010101 010001 101000 110010 111010    

ينتج عن عملية التحويل هذه كل بت من المفتاح الأولي المستخدم في حوالي 14 من 16 مفتاح فرعي ، على الرغم من استخدام بعض وحدات البتات أكثر قليلاً من غيرها.

التقليب الأولي

بمجرد أن يتم تقسيم البيانات إلى كتل ومبطنة إذا لزم الأمر ، فقد حان الوقت لبدء عملية تشفير DES. سنعود إلى المفاتيح الفرعية التي أنشأناها للتو في مرحلة لاحقة. تُعرف الخطوة الأولى باسم التقليب الأولي ، حيث يتم إعادة ترتيب البيانات وفقًا للجدول التالي:

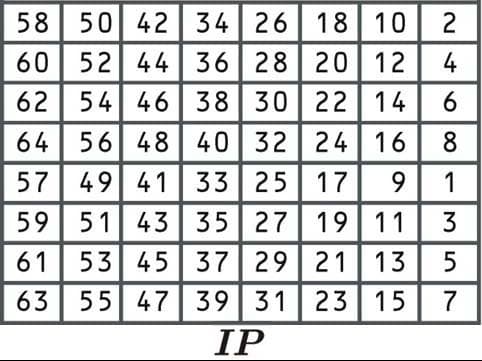
عملية التقليب الأولية هذه لا تجعل الخوارزمية أكثر أمانًا. هذا لأنه لا يتضمن إدخال أي مفتاح ، ويمكن عكسه بسهولة. تم تصميم الخوارزمية في الأصل بهذه الطريقة لأنها جعلت التنفيذ أسهل في سياقات معينة.

نظرًا لأننا قمنا بتغطية التباديل عدة مرات ، فسنتخطى أي تفسير رئيسي هنا. العودة الى الجدول الزمني DES الرئيسية القسم إذا كنت بحاجة إلى مزيد من المعلومات حول كيفية عملها.

دعنا نأخذ الكتلة الأولى من الرسالة “هيا بنا نذهب إلى الشاطئ” ، والتي استمدناها من منع قسم تحت فهم خوارزمية DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

منذ تقول الخلية الأولى 58, سنختار الرقم من المركز 58:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

ثم نأخذ الرقم من المركز 50:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

والرقم من المركز 42:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

هذا يعطينا “110” إلى هذا الحد. سنشكل بقية الرقم:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

عند اكتمال التقليب الأولي ، يتم نقل البيانات إلى الخطوة التالية.

تقسيم الكتل

بمجرد أن مرت البيانات التقليب الأولي ، يتم تقسيمها إلى نصفين. نأخذ كتلة لدينا التي خضعت للتو التقليب الأولي:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

وسنقوم بفصلها إلى كتلتين ، كتلة يسرى (مكونة من أول 32 رقمًا) ، والمعروفة باسم L0:

L0    11010111 01001010 10101000 10011101

والكتلة اليمنى (تتكون من الأرقام 32 الثانية) ، والمعروفة باسم R0:

R0    01001011 10110101 10000111 10101001

وظيفة F

الآن وقد تم تقسيم الكتلة ، فقد حان الوقت لإحداث وظيفة F. في الجولة الأولى ، سيتم تطبيقه فقط على النصف الأيمن من الكتلة ، بينما يبقى النصف الأيسر جانباً حتى وقت لاحق. يخضع الجانب الأيمن للخطوات الأربع التالية كجزء من وظيفة F:

• التقليب التوسعي (E في المخطط)
• خلط المفتاح (⊕ في المخطط)
• استبدال (كل S1 ، S2 وما إلى ذلك في الرسم التخطيطي)
• التقليب (P في المخطط)

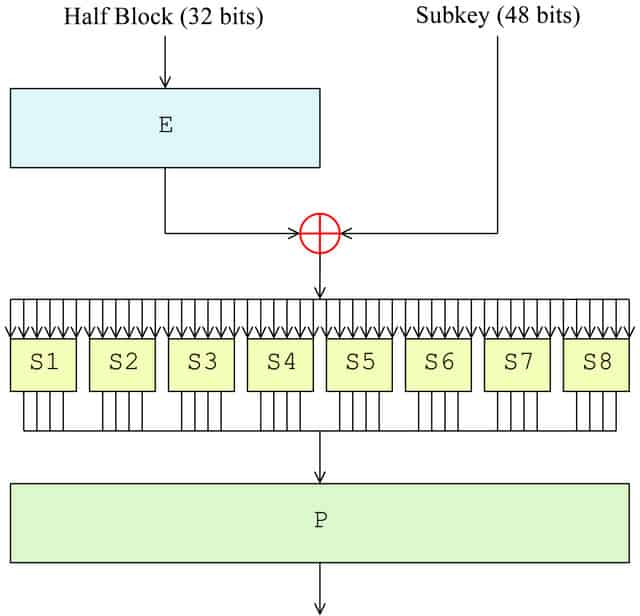
توسع التقليب

إن التقليب التوسعي ينجز ثلاثة أشياء. الأهم من ذلك أنه يسمح بتات واحدة من بيانات الإدخال للتأثير على إخراج اثنين من البتات الأخرى ، مما تسبب في تأثير الانهيار. كما أنه يجعل النصف الأيمن 48 بت ، بحيث يكون بنفس حجم المفتاح الفرعي للخطوة التالية. التأثير الآخر من التقليب التوسعي هو أنه يجعل الإخراج أطول من الإدخال. هذا يسمح لها بالضغط في عملية الاستبدال.

يتم إعادة ترتيب البتات وفقًا للجدول التالي. بعض البتات الفردية موجودة في الجدول مرتين ، وهي كيفية توسيع الكتلة من 32 إلى 48 بت:

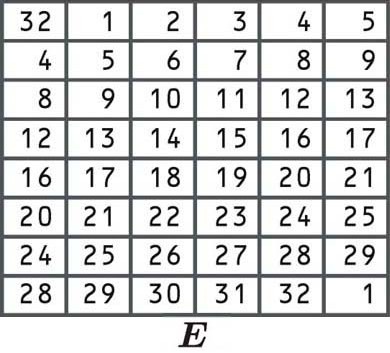
نظرًا لأن الخلية الأولى تشير إلى 32 ، فإننا نأخذ الكتلة اليمنى ونختار الرقم من الموضع 32 ، تمامًا كما فعلنا في الأمثلة الأخرى من التقليب المذكورة أعلاه:

R0    01001011 10110101 10000111 10101001

ثم نأخذ الأرقام من الموضع الأول ، والموضع الثاني ، وما إلى ذلك ، إلى أعلى حتى نصل إلى الركن الأيمن السفلي من الكتلة. لأن هناك 1 في هذه الخلية ، سيكون الرقم الأخير أيضًا هو الرقم الذي يظهر في الموضع الأول من الكتلة.

دعنا نقول أن التقليب التوسعي يعطينا كتلة 48 بت جديدة من:

101110 100110 100100 000000 001100 001110 101101 011110

خلط المفتاح

بمجرد توسيع الكتلة إلى 48 بت ، فقد حان الوقت لتطبيق المفتاح الفرعي للجولة الأولى ، والذي استمدناه منه الجدول الزمني DES الرئيسية القسم أعلاه. يتم تعديل الكتلة بواسطة المفتاح الفرعي باستخدام تشفير XOR.

تشفير XOR هو تشفير إضافي يتبع عملية بسيطة ، لا سيما عند مقارنته بالعناصر الأخرى التي ناقشناها بالفعل.

في تشفير XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

لذلك ، دعنا نقول أنه يتعين على XOR الرقمين التاليين بالثنائي:

1101

0101

ستتم إضافة كل رقم إلى الرقم الموجود تحته. وفقًا للقواعد الثلاثة الموضحة أعلاه ، فإن هذا يعطي نتيجة لما يلي:

1000

لإكمال خطوة خلط المفاتيح ، نأخذ الجانب الأيمن من المجموعة التي قمنا بتوسيعها للتو إلى 48 بت ، والمفتاح الدائري الأول. نقوم بعد ذلك بإضافة XOR:

منع:                      101110 100110 100100 000000 001100 001110 101101 011110

جولة مفتاح واحد:     010101 010101 101010 110100 101001 100101 101010 101010

نتيجة XOR:             111011 110011 001110 110100 100101 101011 000111 110100

ثم يتم تمرير نتيجة العملية XOR إلى الجولة التالية.

الاستبدال

استبدال يضيف الارتباك إلى البيانات. تتم عادةً باستخدام جداول البحث ، والتي تُعرف أيضًا باسم صناديق الاستبدال أو S-boxes. تستخدم DES ثمانية جداول منفصلة أو مربعات S ، مختلفة لكل 6 بتات من البيانات. يوضح الجدول التالي الصناديق الثمانية الخاصة بـ DES:

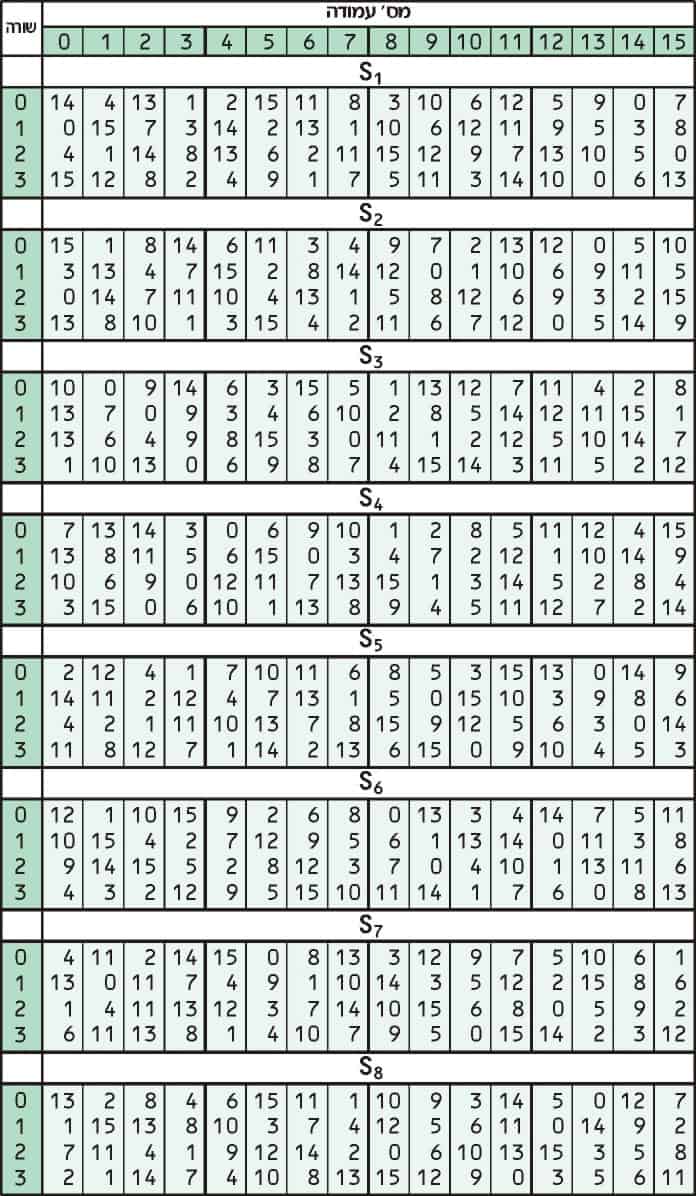
تُستخدم مربعات S الثمانية المنفصلة لترجمة كل إدخال من 6 بتات إلى إخراج 4 بت. الخطوة الأولى في العملية هي أخذ الأرقام في بداية ونهاية شريحة 6 بت ، ثم تحويل هذه القيمة الثنائية إلى رقم عشري.

دعنا نأخذ البيانات التي انتهينا للتو من XORing في الخطوة السابقة:

111011 110011 001110 110100 100101 101011 000111 110100

سوف نلقي نظرة على الجزء الأول المكون من 6 بت لتوضيح كيفية عمل عملية الاستبدال:

111011

منذ الرقم الأول والرقم الأخير على حد سواء 1, هذا يعطينا قيمة 11. نحن ثم تحويل 11 من ثنائي إلى عشري ، والذي يعطينا 3. هذه مجرد قيم مكافئة ، مكتوبة بطرق مختلفة. فكر في الأمر على أنه تحويل لغة الكمبيوتر إلى لغة بشرية. يمكنك التحقق من التحويل بنفسك باستخدام آلة حاسبة على الإنترنت إذا كنت تريد ذلك.

ثم نأخذ الأرقام الأربعة الوسطى للجزء 6 بت الأول:

111011

وتحويلها من ثنائي إلى عشري. 1101 يترجم إلى رقم 13.

الآن ، نأخذ هذين الرقمين وننظر إليهما في س1 الطاولة:

               

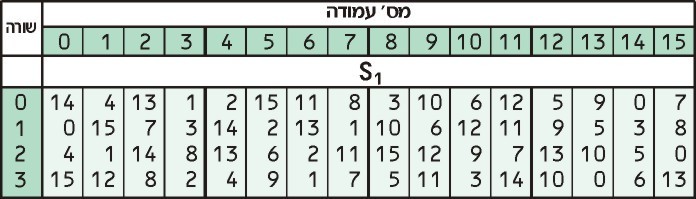
الرقم الأول لدينا, 3, يخبرنا أن ننظر في الصف الثالث ، في حين أن الرقم الثاني لدينا, 13 يخبرنا أن ننظر في العمود 13th. القيمة في الصف الثالث من العمود الثالث عشر هي 0.

الآن وبعد أن بحثنا عن رقمنا في الجدول ، نقوم بتحويله إلى رقم ثنائي مكون من أربعة أرقام. عادةً ما يتم كتابة صفر كـ 0 في ثنائي ، ولكن 0000 هو نفسه ، وهذا هو التنسيق الأكثر ملاءمة لأغراضنا.

بعد هذه العملية ، يحوّل S-box أول قسم من البيانات من 6 بتات لدينا (111011) في قيمة مختلفة 4 بت (0000). يبدو معقدًا ، لكن هذه التقنية تساعد على زيادة حجب العلاقة بين النص المشفر والنص الشائع الذي يرتبط به.

يمر الجزء التالي من البيانات المكون من 6 بتات بنفس العملية ، ولكنه بدلاً من ذلك يستخدم المربع S2 الموضح أعلاه. يستخدم القسم الثالث جدول S3 وما إلى ذلك ، حتى يخضع القسم الأخير للاستبدال من خلال جدول S8.

مرة أخرى ، سنخدع لبقية القيم. دعنا نقول أن صناديق الاستبدال تعطينا نتيجة:

0000 1010 1100 1001 0100 1001 0111 0001

بمجرد مرور كل قسم من البيانات عبر المربع S-box ، ينتقل إلى الخطوة التالية.

تبديل

المرحلة الأخيرة من الدالة F هي التقليب الآخر ، باستخدام الجدول التالي: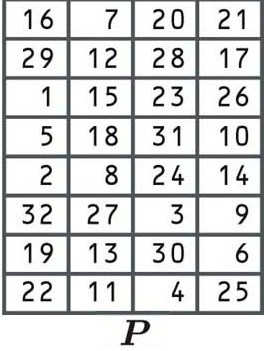

الآن ، يجب أن يكون لديك فهم جيد لكيفية تحويل التباديل للأرقام من الكتلة القديمة إلى موضع مختلف في الكتلة الجديدة ، لذلك لن نذهب إليها مرة أخرى.

دعنا نقول أن هذا التقليب يأخذ النتيجة السابقة لدينا:

0000 1010 1100 1001 0100 1001 0111 0001

ويعطينا ناتج من:

0101 0110 1001 0101 0010 0100 0101 0010

الآن وبعد اكتمال التقليب ، انتهينا من الخطوات الأربع لوظيفة F في هذه الجولة. في التدوين الرياضي ، تعرف هذه القيمة باسم و (R0, ك1). هذا يعني أن النتيجة هي الوظيفة (F) من الجانب الأيمن الأولي من الكتلة (R0) والمفتاح الفرعي للجولة الأولى (ك1).

XOR مع الكتلة اليسرى

تذكر كيف قسمنا الكتلة إلى النصف قبل أن نبدأ خطوات الدالة F؟ وضعنا الجانب الأيسر من الكتلة (L0) جانباً ، بينما خضع الجانب الأيمن لكل من هذه العمليات. حسنًا ، لقد حان الوقت ليعود L0 إلى العمل.

نحن نأخذ الجانب الصحيح الذي قمنا بمعالجته للتو و (R0, ك1) وأضفه إلى الجانب الأيسر القديم (L0) باستخدام التشفير XOR. هذا يعطينا R1, نتيجة جولتنا الأولى:

و (R0, ك1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0:                                    1101 0111 0100 1010 1010 1000 1001 1101

نتيجة XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

الرجوع إلى خلط المفتاح القسم أعلاه إذا كنت بحاجة إلى تذكير بكيفية عمل تشفير XOR.

15 جولة أخرى …

إذا وصلت إلى هذا الحد ، فمن المحتمل أن عملية التصميم قد تبدو عملية شاقة. لكنها ليست قريبة من الانتهاء حتى الآن. تنتقل البيانات عبر الخطوات الأربع لوظيفة F ، تليها XOR ، 15 مرة أخرى ، ليصبح المجموع 16 جولة.

في الجولة الثانية ، نأخذ النسخة الأصلية التي لم يمسها الجانب الأيمن من الكتلة (R0) ونجعلها الجانب الأيسر الجديد (L1). في هذه الأثناء ، نأخذ نتيجة جولتنا الأولى ونرسلها عبر الدالة F. يحدث كل شيء كما حدث في المرة الأخيرة ، ولكن في هذه المرة يتم استخدام المفتاح الفرعي للجولة الثانية بدلاً من ذلك. دعنا نقول أن هذه العملية تعطينا نتيجة:

و (R1, ك2):        1011 0111 1000 1011 1001 1101 1001 1110

نحن ثم XOR النتيجة مع L1 ، والذي هو في الواقع R0 (اشتقنا هذا في كتل تقسيم الجزء). هذا يعطينا نتيجة الجولة الثانية ، R2:

و (R1, ك2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

قد تبدو هذه الخطوة مربكة بعض الشيء ، ولكن في ظل مخطط Feistel ، يصبح الجانب الأيمن القديم هو اليسار الجديد ، بينما تصبح نتيجة العملية هي الجانب الأيمن الجديد.

يمنحك الرسم البياني التالي تمثيلًا مرئيًا لما يحدث. يمثل IP التقليب المبدئي ، F عبارة عن وظيفة احتياطية لكامل الدالة F ، والرمز function يرمز إلى وظيفة XOR والأسهم تشير إلى أن كل جانب من جوانب الكتلة يتحرك بين اليسار واليمين:

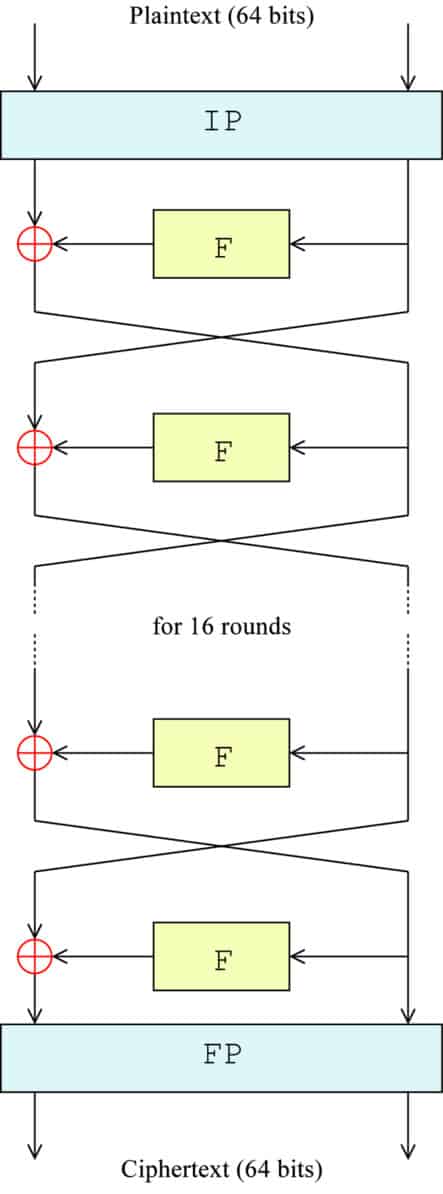
الصيغة الدقيقة لكل خطوة هي:

Lن = Rن 1

Rن = Lن 1 + F(Rن 1,كن)

أين:

L = النصف الأيسر من الكتلة (يبدأ بـ L0 عند تقسيم الكتلة في البداية)

R = النصف الأيمن من الكتلة (يبدأ بـ R0 عند تقسيم الكتلة في البداية)

n = رقم الجولة (يبدأ بـ 0 ، عندما تم تقسيم الكتلة في البداية)

و = وظيفة F

Kn = المفتاح الفرعي للجولة n

وفقًا للصيغة والمخطط ، في الجولة الثالثة ، يصبح R1 هو النصف الأيسر الجديد (L2) ، بينما تتم معالجة R2 من خلال الدالة F. دعنا نقول أنه يعطينا نتيجة:

و (R2, ك3)        1001 0111 0000 1011 1101 0111 1011 1011

بعد ذلك نحسب نتيجة جولتنا الثالثة (R3) ، باستخدام تشفير XOR ، تمامًا كما كان من قبل:

و (R2, ك3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

تستمر نفس العملية حتى الجولة الخامسة عشرة ، مع تبديل الكتل واستخدام المفتاح الفرعي التالي في كل جولة. في الجولة 16 والأخيرة ، لا يتم تبديل الكتل. بدلاً من ذلك ، يتم دمجها لتشكيل كتلة 64 بت. الامتناع عن تبديل الكتل في هذه المرحلة الأخيرة يسمح باستخدام الخوارزمية لكل من التشفير وفك التشفير.

دعنا نقول أن الجولة النهائية تعطينا نتيجة:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

التقليب النهائي

هذا التقليب هو عكس التقليب الأولي ، ومرة ​​أخرى ، فإنه لا يضيف قيمة أمان إضافية. يقوم بإعادة ترتيب البيانات وفقًا للجدول التالي:

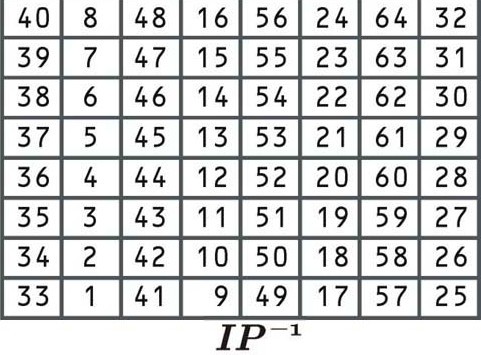
هذا الجدول التقليب يعمل نفس الجداول السابقة. نظرًا لأنها الخطوة الأخيرة في عملية التشفير ، ستكون النتيجة هي النص المشفر للكتلة الأولى من “لنذهب الى الشاطئ”. دعنا نقول أن الكتلة المشفرة هي:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

الآن ، إذا كنت تريد النص المشفر الحقيقي لـ “دعنا نذهب إلى الشاطئ” ، فيمكنك فقط تخطي عملية التعلم بأكملها وانتقلت مباشرةً إلى أداة تشفير DES عبر الإنترنت. إذا أدخلنا الجملة إلى جانب مفتاح (دعنا نقول kj329nf982bc9wn1) تعطينا الأداة نصًا مشفرًا:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

إذا كنت ترغب في ذلك ، يمكنك عندئذٍ تحويل المفتاح ونص التشفير إلى ثنائي ثم مقارنة كيفية استخدام نص المجموعة الأولى يصطف مع العملية برمتها التي تم تحديدها.

DES فك التشفير

في DES ، عملية فك التشفير واضحة بشكل لا يصدق. تسمح بنية Feistel للخوارزمية بعكسها بسهولة. يتم تشغيل العملية نفسها تقريبًا لفك تشفير المعلومات. الفرق الوحيد هو أن المفاتيح الفرعية يتم تطبيقها في الاتجاه المعاكس. هذا إعداد فعال ، لأنه يعني أنه يمكن استخدام نفس البرنامج والأجهزة في كل من عمليات التشفير وفك التشفير.

لفك تشفير البيانات ، يمر أولاً من خلال التقليب الأولي ، ثم يتم تقسيم الكتلة والنصف الأيمن يمر عبر الدالة F. الفرق هو أنه في الجولة الأولى من فك التشفير ، يتم تطبيق المفتاح الفرعي السادس عشر. كل شيء آخر العائدات كالمعتاد. بمجرد اكتمال وظيفة F ، يتم XORed مع الجانب الأيسر من الكتلة.

يتم تبديل الكتل وتنتقل النتيجة خلال نفس العملية للجولة الثانية ، باستثناء أن المفتاح الفرعي الخامس عشر يتم تطبيقه. تستمر هذه العملية حتى الجولة 16 ، عند استخدام المفتاح الفرعي الأول.

تمامًا كما هو الحال في عملية التشفير ، لا يتم تبديل الكتل في المرحلة النهائية ، ثم تخضع البيانات إلى التقليب النهائي. هذا ينتهي عملية فك التشفير ، مما أدى إلى النص الأصلي للرسالة.

3DES

نظرًا لأن نقاط الضعف الأمنية في DES أصبحت أكثر وضوحًا ، تم اقتراح 3DES كوسيلة لتوسيع حجم المفتاح دون الحاجة إلى إنشاء خوارزمية جديدة تمامًا. بدلاً من استخدام مفتاح واحد كما هو الحال في DES ، يقوم 3DES بتشغيل خوارزمية DES ثلاث مرات ، مع ثلاثة مفاتيح 56 بت:

• مفتاح واحد يستخدم ل تشفير الشرير.
• يستخدم المفتاح الثاني ل فك النص الذي تم تشفيره بواسطة مفتاح واحد.
• المفتاح الثالث يستخدم ل تشفير النص الذي تم فك تشفيره بواسطة المفتاح الثالث.

في كل مرحلة ، يتم اتباع عملية DES كاملة كما هو موضح أعلاه.

الآن ، قد تتساءل “كيف يمكن لتطبيق فك التشفير في الخطوة الثانية تعزيز الأمن؟”

الجواب هو أنه يستخدم مفتاح منفصل. إذا تم استخدام المفتاح الأول أيضًا لفك تشفير البيانات في الخطوة الثانية ، فستعود البيانات إلى حيث بدأت.

ومع ذلك ، نظرًا لأنه يستخدم مفتاحًا مختلفًا ، فإن عملية فك التشفير لا تعمل فعليًا على فك تشفير البيانات. قد يبدو هذا شاذًا منطقيًا ، ولكن فك تشفيره باستخدام مفتاح منفصل لا يؤدي إلا إلى خلط البيانات بشكل أكبر.

بمجرد أن يقوم المفتاح الثاني “بفك تشفير” البيانات ، يتم تطبيق المفتاح الثالث لتشفيرها مرة أخرى. والنتيجة هي النص المشفر ثلاثي الأبعاد.

تم تصميم 3DES بهذه الطريقة لأنه يسمح للتطبيقات بأن تكون متوافقة مع مفتاح DES واحد ، مفتاحان DES وثلاثة مفتاح DES (يتم تغطيتها في القسم التالي). لن ينجح هذا إذا تم استخدام التشفير في الخطوات الثلاث.

خيارات قفل 3DES

من الناحية الفنية ، يمكن تطبيق 3DES بثلاثة تكوينات مفاتيح مختلفة. على الرغم من ذلك ، فإن الخيارين الثاني والثالث غير آمنين ويجب عدم تنفيذهما أبدًا.

• خيار القفل واحد – يستخدم هذا الخيار ثلاثة مفاتيح مستقلة وهو الأكثر أمانًا.
• خيار القفل الثاني – في هذا التكوين ، مفاتيح الأول والثالث هي نفسها.
• خيار القفل ثلاثة – هذا يستخدم ثلاثة مفاتيح متطابقة. عند استخدام مفاتيح متطابقة ، تلغى عملية فك التشفير في المرحلة الثانية التشفير الأول ، تاركة فقط التشفير النهائي لتغيير البيانات. وهذا يجعل النتيجة نفس DES العاديين.

عملية 3DES: خيار القفل واحد

لنكن صادقين ، فكل عملية 3DES يمكن أن تجعل رأسك يدور ، خاصة إذا كنت جديدًا في التشفير. لمساعدته على الدخول ، إليك ملخص موجز لنظام التشفير بأكمله لخوارزمية 3DES:

يدخل النص العادي خوارزمية 3DES وهو الأول مشفرة مع مفتاح واحد في الخطوات التالية:

• • مفتاح الجدول الزمني – يتم استخلاص المفاتيح الفرعية 16 من مفتاح واحد

  • التقليب الأولي

  • يتم تقسيم الكتلة إلى نصفي اليسار واليمين

• • • يتم إرسال النصف الأيمن من خلال الدالة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • اجعل الجانب الأيمن القديم هو الجانب الأيسر الجديد ، والنتيجة هي الجانب الأيمن الجديد

      كرر الخطوات المذكورة أعلاه 14 مرة

• • • يتم إرسال النصف الأيمن من خلال الدالة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة 16

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • الجمع بين الجانبين الأيسر والأيمن من كتلة معا

• • التقليب النهائي

خذ النص الذي تم تشفيره باستخدام المفتاح الأول ، ثم أرسله عبر عملية “فك التشفير” مع مفتاح اثنان:

• • الجدول الزمني الرئيسي – يتم استخلاص المفاتيح الفرعية 16 من المفتاح الثاني

  • التقليب الأولي

  • يتم تقسيم الكتلة إلى نصفي اليسار واليمين

• • • يتم إرسال النصف الأيمن من خلال وظيفة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة (بدءًا من المفتاح الفرعي السادس عشر لفك التشفير)

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • اجعل الجانب الأيمن القديم هو الجانب الأيسر الجديد ، والنتيجة هي الجانب الأيمن الجديد

      كرر الخطوات المذكورة أعلاه 14 مرة

• • • يتم إرسال النصف الأيمن من خلال الدالة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة الأولى

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • الجمع بين الجانبين الأيسر والأيمن من كتلة معا
  • التقليب النهائي

خذ البيانات التي تم “فك تشفيرها” بواسطة المفتاح الثاني ، ثم أرسلها عبر أونعملية التشفير مع مفتاح ثلاثة:

• • مفتاح الجدول الزمني – 16 مفاتيح فرعية مستمدة من المفتاح الثالث

  • التقليب الأولي

  • يتم تقسيم الكتلة إلى نصفي اليسار واليمين

• • • يتم إرسال النصف الأيمن من خلال الدالة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • اجعل الجانب الأيمن القديم هو الجانب الأيسر الجديد ، والنتيجة هي الجانب الأيمن الجديد

      كرر الخطوات المذكورة أعلاه 14 مرة

• • • يتم إرسال النصف الأيمن من خلال الدالة F

      • توسع التقليب

      • XOR مع المفتاح الفرعي للجولة 16

      • الاستبدال

      • تبديل

    • XOR نتيجة وظيفة F مع الجانب الأيسر

    • الجمع بين الجانبين الأيسر والأيمن من كتلة معا

• • التقليب النهائي

والنتيجة هي النص المشفر 3DES.

أمن 3DES

يعتمد أمان 3DES على خيار القفل المستخدم. يتضمن خيار Keying one ثلاثة مفاتيح 56 بت مختلفة ، مما يمنحه إجمالي طول مفتاح يبلغ 168 بت. يتم تقليل الطول الفعال بدرجة كبيرة عن طريق الهجمات التي تحدث في المنتصف ، والتي تصل بأمان العالم الحقيقي إلى 112 بت.

تعد الهجمات التي تتم في منتصف الطريق مفيدة ضد مخططات التشفير التي تكرر نفس الخوارزمية عدة مرات. تقوم التقنية بتخزين القيم الفورية من كل مرحلة تشفير ، ثم تستخدم هذه المعلومات لتحسين الوقت الذي تستغرقه عملية حساب الخوارزمية بشكل جذري..

يحتوي الخياران الثاني والثالث على مفاتيح أصغر بشكل كبير ويتعرضان لهجمات غير معروفة ونصًا مختارًا وغيرهما.

من الممكن حدوث هجمات غير معروفة عندما يكون للخصم حق الوصول إلى كل من نص عادي ونص مشفر للرسالة. إذا كانت الخوارزمية عرضة لهذه الهجمات ، فيمكن للمهاجم استخدام هذه المعلومات لاستنتاج المفتاح ، مما يسمح له بتقسيم جميع البيانات الأخرى التي تم تشفيرها بواسطة نفس المفتاح.

يتشابه الهجوم الذي تم اختياره مع النص العادي ، ولكنه ينطوي على قيام المهاجم بالكشف عن المفتاح من خلال مقارنة النصوص المشفرة بالنصوص التعسفية.

نظرًا لوجود نقاط الضعف هذه وإجمالي أحجام المفاتيح الصغيرة التي ينطوي عليها الأمر ، فإن خيارات القفل 2 و 3 غير آمنة ويجب عدم تنفيذها.

هو 3DES آمنة?

نظرًا لأن 3DES سيتم إهمالها في السنوات القليلة المقبلة ، فمن الأفضل استخدام خوارزميات أخرى. على الرغم من أن خيار القفل الأول لا يزال آمنًا للعديد من التطبيقات ، إلا أنه لا توجد أسباب وجيهة كثيرة لاستخدامه بدلاً من بديل مثل AES.

على الرغم من احتفاظ 3DES بمكانة هامة في التشفير كمتابعة لـ DES ، فقد انتهت سنوات مجدها وحان الوقت للمضي قدمًا. إذا كنت ترغب في تأمين أنظمتك في المستقبل ، فيجب عليك استخدام خوارزمية أكثر حداثة بدلاً من ذلك.

ذات صلة: وأوضح أنواع التشفير الشائعة

الخطة العاشرة بواسطة وزارة الدفاع مرخص بموجب CC0