什么是RSA加密，它如何工作？

RSA加密是一种解决曾经是密码学最大问题的系统： 您如何向他人发送编码信息 没有机会与他们先前共享代码?

本文将教您所有需要了解的内容 RSA加密是如何开发的, 怎么运行的, 背后的数学, 它的作用是什么 以及一些 面临的最大安全问题. 了解RSA将为您提供一些基础知识，可帮助您了解我们的在线生活中有多少部分受到保护.

什么是RSA加密?

假设您想告诉您的朋友一个秘密。如果您就在他们旁边，就可以窃窃私语。如果您在该国的对面，那显然是行不通的。您可以将其写下并邮寄给他们，或使用电话，但是 这些通信渠道中的每一个都不安全 任何有足够强烈动机的人都可以轻松拦截消息.

如果这个秘密足够重要，那么您就不必冒着将其写下来的风险了-间谍或流氓邮政员工可能正在查看您的邮件。同样，有人可能会在您不知情的情况下窃听您的电话，并记录您拨打的每个电话.

防止窃听者访问消息内容的一种解决方案是 加密. 这基本上意味着向消息中添加代码，从而将其更改为混乱的混乱。如果您的代码足够复杂，那么只有那些有权访问该代码的人才能访问原始消息。.

如果您有机会事先与您的朋友共享代码，那么 你们两个人都可以随时发送加密的消息, 知道你们两个是唯一能够阅读邮件内容的人。但是，如果您没有机会事先共享代码怎么办?

这是密码学的基本问题之一，已经解决了 RSA之类的公钥加密方案（也称为非对称加密）.

在RSA加密下，邮件使用称为“ a”的代码进行加密。 公钥, 可以公开共享。由于RSA算法具有一些独特的数学特性, 一旦使用公用密钥对邮件进行加密，则只能使用称为私钥的另一个密钥对邮件进行解密. 每个RSA用户都有一个包含其公钥和私钥的密钥对。顾名思义，私钥必须保密.

公钥加密方案与 对称密钥加密，其中加密和解密过程都使用相同的私钥. 这些差异使像RSA这样的公钥加密对于在没有机会预先安全分发密钥的情况下进行通信很有用.

对称密钥算法有其自己的应用程序，例如加密数据供个人使用，或者用于存在可以共享私钥的安全通道时.

也可以看看： 公钥加密

RSA加密在哪里使用?

RSA加密通常用于 与其他加密方案结合, 或 数字签名 可以证明消息的真实性和完整性。它通常不用于加密整个邮件或文件，因为与对称密钥加密相比，它效率较低且资源占用更多.

使事情更有效率, 通常，将使用对称密钥算法对文件进行加密，然后使用RSA加密对对称密钥进行加密. 在此过程中，只有有权访问RSA私钥的实体才能解密对称密钥.

在无法访问对称密钥的情况下， 原始文件无法解密. 此方法可用于确保消息和文件的安全，而不会花费太长时间或消耗太多的计算资源.

RSA加密可以在许多不同的系统中使用。可以在OpenSSL，wolfCrypt，cryptlib和许多其他密码库中实现.

作为最早广泛使用的公共密钥加密方案之一，RSA为我们的许多安全通信奠定了基础。它是 传统上用于 TLS 也是PGP加密中使用的原始算法。在各种网络浏览器，电子邮件，VPN，聊天和其他通信渠道中仍然可以看到RSA.

RSA还经常用于在VPN客户端和VPN服务器之间建立安全连接。在像OpenVPN这样的协议下，TLS握手可以使用RSA算法来交换密钥并建立安全通道.

RSA加密的背景

正如我们在本文开头所提到的，在没有公开密钥加密之前，在公开密钥加密之前进行安全通信是一个挑战。如果没有机会提前共享代码，或者没有安全的渠道可以分配密钥，那么在没有敌人能够拦截和访问消息内容的威胁的情况下，就无法进行通信。.

直到1970年代，情况才真正开始发生变化。詹姆斯·H·埃利斯（James H. Ellis）在本世纪初发表了关于我们现在称为公钥密码学的第一个重大进展。埃利斯（Ellis）找不到实施他的工作的方法，但是他的同事克利福德·考克斯（Clifford Cocks）对其进行了扩展，使其成为我们现在所知道的 RSA加密.

难题的最后一部分就是我们现在所说的 Diffie-Hellman密钥交换. 另一位同事Malcolm J.Williamson提出了一种方案，该方案允许双方共享一个加密密钥，即使该通道正在受到对手的监视.

所有这些工作都是在英国情报机构政府通讯总部（GCHQ）进行的， 将发现分类. 部分由于技术限制，GCHQ当时看不到公共密钥加密的用途，因此开发工作闲散地堆积在架子上. 直到1997年，该作品才被解密，并承认RSA的原始发明者.

几年后，类似的概念开始在公共领域发展。拉尔夫·默克尔（Ralph Merkle）创建了一种早期形式 公钥密码学, 在Diffie-Hellman密钥交换的设计中影响了Whitfield Diffie和Martin Hellman.

Diffie和Hellman的想法缺少一个重要方面，这将使他们的工作成为公共密钥密码学的基础。这是一个 单向函数，将难以反转. 1977年, 罗恩·里维斯特，阿迪·沙米尔和伦纳德·阿德曼, 它的姓氏是RSA的首字母缩写，经过一年的研究后提出了解决方案.

麻省理工学院的学者在1977年逾越节聚会后取得了突破。一夜的饮酒之后，里维斯特回到家，但他没有睡觉，而是整夜狂热地写了一篇论文，正式阐明了他对单向功能的想法。.

这个想法是MIT在1983年获得专利的，但是直到互联网发展初期，RSA算法才开始被广泛采用，成为一种重要的安全工具。.

RSA加密如何工作?

以下内容将有所简化，因为太多的读者可能已被他们的高中数学老师吓到了。为了避免数学过于复杂，我们将 简化一些概念并使用更小的数字. 实际上，RSA加密使用的质数的大小要大得多，并且还有一些其他复杂性.

在我们解释它们如何组合在一起之前，您必须了解几种不同的概念。这些包括 活板门功能，生成素数，卡迈克尔的totient函数 以及涉及的单独流程 计算公钥和私钥 用于加密和解密过程.

活板门功能

RSA加密的前提是算法是 易于在一个方向上计算，但几乎不可能反向. 例如，如果您被告知701,111是两个质数的乘积，您是否能够找出这两个数是什么?

即使使用计算器或计算机，我们大多数人也不知道从哪里开始，更不用说能够找出答案了。但是，如果我们扭转局面，它将变得更加容易。结果是什么：

907 x 773

如果您感到无聊，则可以将电话拨出脑海，或者在脑海中计算出来，得出答案就是前面提到的701111。这个907和773是回答我们第一个问题的质数，这表明某些方程式可以很容易地找出一种方式，但是似乎不可能反向求出.

该方程式另一个有趣的方面是，如果您已经有了另一个质数，则很容易找出其中一个质数。如果告诉您701,111是907乘以另一个质数的结果，则可以使用以下公式计算出另一个质数：

701,111÷907 = 773

由于这些数字之间的关系很容易在一个方向上计算，但是在反向计算上却很难，因此该方程称为 活板门功能. 请注意，虽然上面的示例很难让人理解，但是计算机可以在很短的时间内完成操作.

因此，RSA使用更大的数字。在实际的RSA实现中，素数的大小各不相同，但是在2048位RSA中，它们会合在一起形成617位数字长的密钥。为了帮助您直观地看到它，关键是这个大小的数字：

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

生成素数

上面提到的活板门功能构成了公钥和私钥加密方案如何工作的基础. 它们的属性允许共享公钥，而不会危及消息或泄露私钥. 它们还允许用一个密钥加密数据，而这种方式只能用该对中的另一个密钥解密.

使用RSA加密邮件的第一步是： 生成密钥. 为此，我们需要 两个质数（p 和 q） 通过素数测试选择的。素数测试是一种有效查找素数的算法，例如Rabin-Miller素数测试.

RSA中的质数必须非常大，并且相距较远。较小或靠近的数字更容易破解。尽管如此，我们的示例将使用较小的数字使事情更易于跟踪和计算.

假设素数测试为我们提供了我们上面使用的素数907和773。下一步是发现模数（ñ），使用以下公式：

ñ = p X q

哪里 p = 907并且 q = 773

因此：

ñ = 907 x 773

ñ = 701,111

卡迈克尔的上位功能

一旦我们有了 ñ, 我们用 Carmichael的收费功能：

    λ（ñ）= 厘米 （p − 1, q − 1）

如果您已经接触过数学课本已有一段时间了，那么上面的内容可能会有些令人恐惧。您可以跳过这一部分，只是相信数学可以工作，否则请坚持我们进行更多的计算。将尽可能详细地解释所有内容，以帮助您掌握基础知识.

对于那些不知道的人, λ（n） 代表卡迈克尔（Carmichael）对 ñ, 而 厘米 表示最低公倍数, 这是两者中最低的数字 p 和 q 可以分为。有几种不同的方法可以解决这个问题，但是最简单的方法就是信任在线计算器为您完成方程式。因此，让我们将数字放入等式中：

    λ（701,111）= 厘米 （907 − 1, 773 − 1）

    λ（701,111）= 厘米 （906, 772）

   使用上面链接的计算器，这使我们：

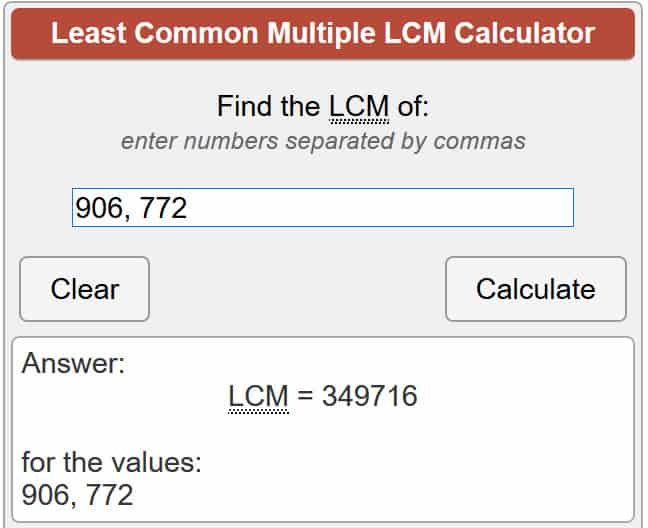
    λ（701,111）= 349,716

生成公钥

现在我们有了Carmichael的素数， 是时候弄清楚我们的公钥了. 根据RSA, 公钥由素数组成 Ë, 以及 ñ. 号码 Ë 可以是1到的值之间的任何值 λ（ñ），在我们的示例中为349,716.

由于公开密钥是公开共享的，因此对于 Ë 成为一个随机数。在实践中, Ë 通常设置为 65,537, 因为当随机选择大得多的数字时，加密效率会大大降低。对于今天的示例，我们将使数字保持较小，以使计算效率更高。假设：

Ë = 11

我们最终的加密数据称为密文（C）。我们从明文消息中得出该消息（米），通过使用以下公式应用公钥：

C = 米Ë 模式

我们已经想出了 Ë 而且我们知道 ñ 也一样我们唯一需要解释的是 模. 这有点超出本文的深度，但它指的是 模运算, 从本质上讲，这意味着当您将一侧分开时剩下的剩余部分。例如：

10 模 3 = 1

这是因为3变成10的三倍，余数为1.

回到方程式。为了简单起见，假设 消息（米）我们想要加密并保密的只是一个数字, 4. 让我们插入所有内容：

C = 米Ë 模 ñ

C = 411 模 701,111

C = 4,194,304 模 701,111

再次，使 模运算 容易，我们将使用在线计算器，但是欢迎您自己解决。通过在在线计算器中输入4,194,304，可以得到：

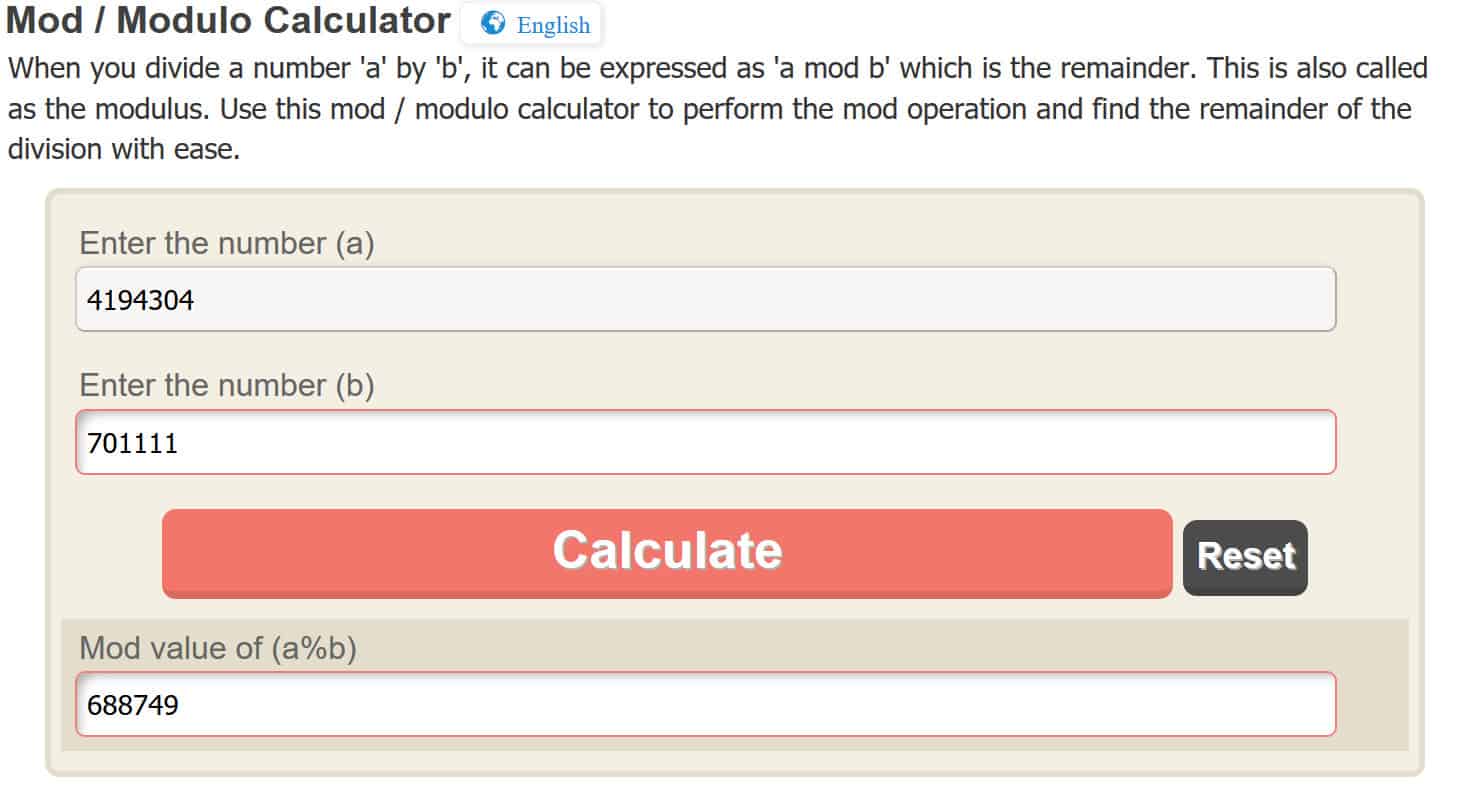
c = 688,749

因此，当我们使用RSA加密邮件时, 4, 用我们的公钥，它给我们 密文688,749. 前面的步骤似乎在数学上有点繁重，但重要的是要重申实际发生的情况.

我们有一个 消息4, 我们想保密。我们对其应用了公开密钥， 加密结果688,749. 现在它已加密, 我们可以安全地将数字688,749发送给密钥对的所有者. 他们是唯一能够使用其私钥对其解密的人。当他们解密它时，他们会看到我们真正发送的消息, 4.

生成私钥

在RSA加密中，一旦使用公共密钥将数据或消息转换为密文，就只能使用同一密钥对中的私有密钥对其进行解密。. 私钥包括 d 和 ñ. 我们已经知道 ñ, 然后使用以下方程式 d：

d = 1 /Ë 模λ（ñ）

在里面 生成公钥 上面的部分中，我们已经决定在示例中, Ë 等于11。同样，我们知道 λ（ñ）等于我们早些时候的工作349,716 卡迈克尔的上位功能. 当我们遇到公式的这一部分时，事情会变得更加复杂：

1 /Ë 模

这个方程可能看起来像是要您将1除以11，但事实并非如此。相反，这仅表示我们需要计算 模逆 的 Ë （在本例中为11）和 λ（ñ）（本例中为349,716）.

这实质上意味着 而不是执行标准的模运算，我们将使用反函数. 通常可以在扩展欧几里得算法中找到它，但这超出了本文的范围，因此我们将作弊并改为使用在线计算器。现在我们了解了所发生的一切，让我们将信息插入公式中：

d = 1 /11 模 349,716

要执行此操作，只需输入11（或您可能拥有的任何值 Ë 如果您使用自己的示例尝试此操作） 整数 和349,716（或您可能拥有的任何值 λ（ñ）（如果您使用自己的示例尝试此操作） 模数 在上面链接的在线计算器中。如果正确完成操作，则应获得以下结果：

d = 254，339

现在，我们具有以下价值 d, 我们可以使用以下公式解密使用公钥加密的邮件：

米 = Cd 模式

现在，我们可以回到在 生成私钥 部分。当我们使用公钥加密消息时，它为我们提供了一个 C 688,749. 从上面我们知道 d 等于254,339. 我们也知道 ñ 等于701,111. 这给了我们：

米 = 688,749254,339 模 701,111.

您可能已经注意到，对于大多数普通计算器而言，尝试将数字取第254,339的幂可能会有点大。相反，我们将使用在线RSA解密计算器。如果您想使用另一种方法，则可以像往常一样施加功率，并以与我们在方法中相同的方式执行模运算。 生成公钥 部分.

在上面链接的计算器中，输入701,111 供应模数：N, 254,399上面写着 解密密钥：D, 还有688,749 数字形式的密文消息, 如下所示：

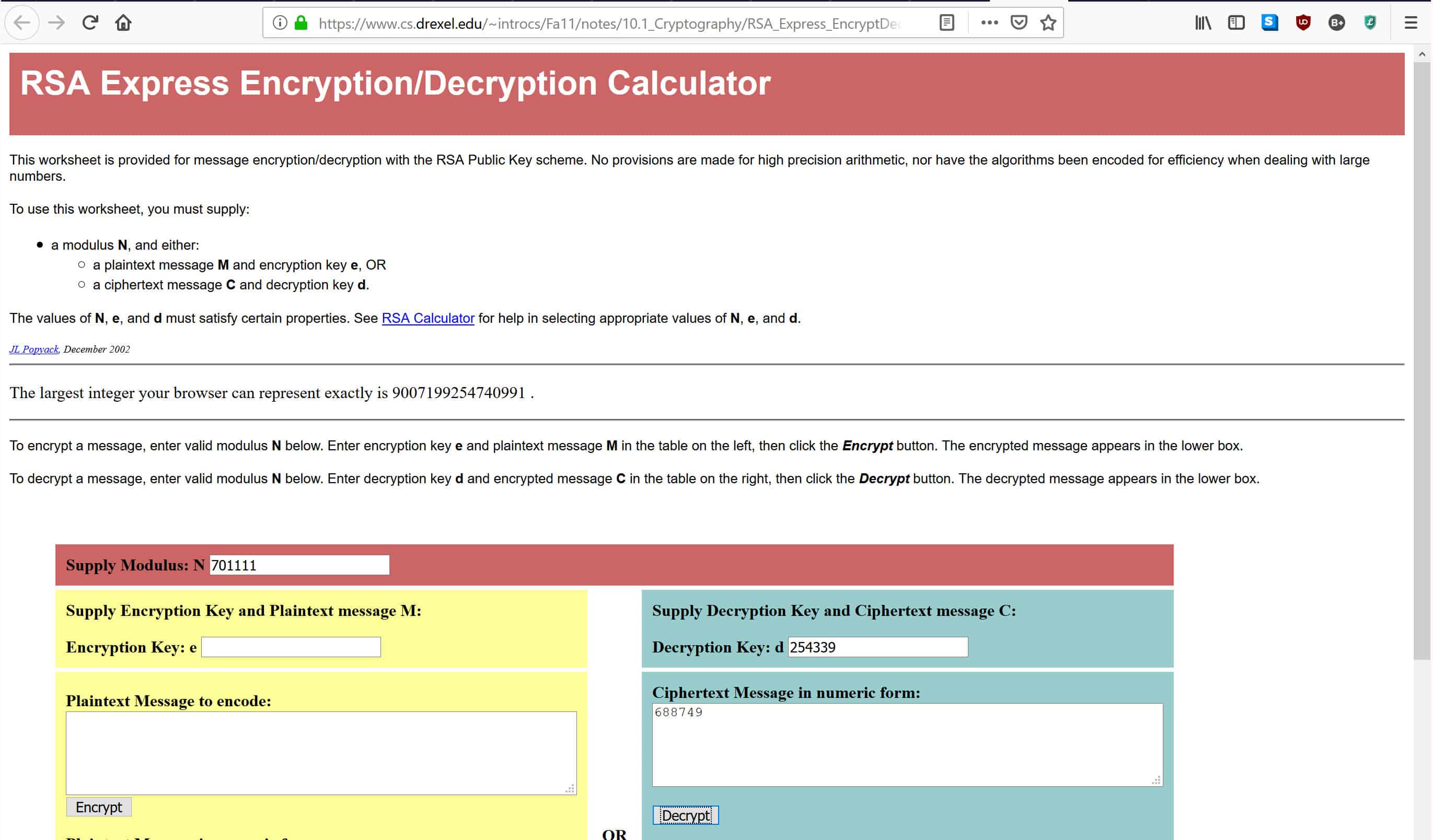
输入数据后，点击 解密, 它将通过上面列出的解密公式来计算数字。这将在下面的框中为您提供原始消息。如果您正确完成了所有操作，则应该得到以下答案 4, 这是我们使用公钥加密的原始消息.

RSA加密如何实际运作

以上各节应该使您对公用密钥加密背后的数学原理有一个合理的了解。可能会有些混乱，但是即使是那些不了解方程式复杂性的人也可以希望从中获得一些有关该过程的重要信息.

在上面列出的步骤中，我们展示了两个实体如何可以安全地通信而无需事先共享代码。首先，他们每个人都需要 设置自己的密钥对 和 彼此共享公钥. 这两个实体需要对其私钥保密，以确保其通信安全.

一旦发送者拥有接收者的公钥，他们就可以使用它来加密他们想要保持安全的数据. 用公用密钥加密后，只能用同一密钥对中的专用密钥解密. 甚至同一公共密钥也不能用于解密数据。这是由于 活板门功能 我们上面提到的.

收件人收到加密的消息时，将使用其私钥访问数据。如果收件人希望以安全的方式退回通讯, 然后，他们可以使用与之通信的一方的公钥对消息进行加密. 同样，一旦使用公钥加密了信息，唯一可以访问信息的方法就是通过匹配的私钥.

这样，以前未知的方可以使用RSA加密在彼此之间安全地发送数据。我们在在线生活中使用的交流渠道的重要组成部分就是以此为基础.

如何使用RSA加密更复杂的消息?

在我们的示例中，我们简化了很多事情以使其更易于理解，这就是为什么我们仅加密消息“ 4”的原因。能够加密数字4似乎并不是特别有用，所以您可能想知道 如何加密更复杂的数据集, 例如对称密钥（这是RSA的最常用用法），甚至是一条消息.

有人可能会困惑于如何使用RSA这样的算法来加密诸如“ n38cb29fkbjh138g7fqijnf3kaj84f8b9f…”之类的密钥或诸如“给我买三明治”之类的消息，该算法处理数字而不是字母。现实情况是，我们计算机处理的所有信息都以二进制（1和0）存储，并且我们使用诸如 ASCII或Unicode 以人类可以理解的方式代表他们（字母）.

这意味着 像“ n38cb29fkbjh138g7fqijnf3kaj84f8b9f…”之类的消息和“给我买三明治”之类的消息已经作为数字存在, 可以使用RSA算法轻松计算。它们所代表的数字更大并且更难于管理，这就是为什么我们更喜欢处理字母数字字符而不是一堆二进制数字的原因.

如果你想 使用RSA加密更长的会话密钥或更复杂的消息，它只会涉及更大的数量.

填充

实施RSA后，它会使用称为 填充以帮助防止多种攻击. 为了解释它是如何工作的，我们将从一个示例开始。假设您正在向朋友发送编码消息：

亲爱的卡伦,

    我希望你一切都好。我们明天还在吃饭吗?

    此致,

    詹姆士

假设您以一种简单的方式对消息进行了编码， 将每个字母更改为字母后面的字母. 这会将消息更改为：

Efbs Lbsfo,

    J ipqf zpv bsf xfmm。 bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    克恩夫特

如果您的敌人截获了这封信，他们可以使用一种技巧来尝试破解密码。他们可以 查看信件的格式，然后尝试猜测消息可能在说什么. 他们知道人们通常以“ Hi”，“ Hello”，“ Dear”或其他一些约定开头.

如果他们尝试使用“ Hi”或“ Hello”作为第一个单词，他们会发现该单词不适合字符数。然后，他们可以尝试“亲爱的”。合适，但这并不一定意味着什么。攻击者只需尝试一下，看看它是什么导致的。因此，他们将分别用“ d”，“ e”，“ a”和“ r”更改字母“ e”，“ f”，“ b”和“ s”。这将给他们：

亲爱的Laseo,

    J ipqe zpv是xemm。是Xe Tujmm Iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    卡内特

它看起来仍然很混乱，因此攻击者可能会尝试查看其他一些约定, 就像我们总结信件的方式. 人们经常在结尾处添加“来自”或“亲切的问候”，但是这些都不适合该格式。相反，攻击者可能会尝试“真诚地为您”，并替换其他字母以查看将其发送到何处。通过将“ z”，“ p”，“ v”，“ t”，“ j”，“ o”，“ d”和“ m”更改为“ y”，“ o”，“ u”，“ s”，“ i”，“ n”，“ c”和“ l”，它们将分别得到：

亲爱的拉森,

    我，你很生气。是Xe Tuill Iawinh dinnes uonossox?

    此致,

    卡内特

修改之后，攻击者似乎开始行动起来。他们除了最初的猜测外还找到了“ I”，“ you”和“ are”.

攻击者看到这些单词的语法顺序正确无误，可以确信自己正朝着正确的方向前进。到现在为止，他们可能还已经意识到，涉及每个字母的代码都被更改为字母后面的字母。. 一旦他们意识到这一点，就可以轻松翻译其余内容并阅读原始消息.

上面的示例只是一个简单的代码，但是如您所见, 消息的结构可以为攻击者提供有关其内容的线索. 当然，很难从消息的结构中找出消息，并且进行了一些有根据的猜测，但是您需要记住，计算机比我们更擅长于此. 这意味着它们可用于在更短的时间内找出更复杂的代码, 基于来自结构和其他元素的线索.

如果结构可能导致代码被破解并泄露消息的内容，那么我们需要某种隐藏方法来保持消息的安全。这使我们 填充.

填充邮件时, 添加随机数据以隐藏原始格式提示，这可能导致加密邮件被破坏. 使用RSA时，事情要复杂一些，因为加密密钥没有明显的字母格式，这可以帮助我们在上面的示例中找到线索.

尽管如此，攻击者仍可以使用多种攻击来利用代码的数学特性并破坏加密的数据。由于这种威胁, RSA的实现使用诸如OAEP之类的填充方案将额外的数据嵌入到消息中. 在加密邮件之前添加此填充，使RSA更加安全.

签名消息

RSA不仅可以用于加密数据，还可以用于其他用途。它的特性也使其成为一个有用的系统 确认声称已发送消息的实体已发送消息，并证明消息未被更改或篡改.

当某人想要证明其消息的真实性时，他们可以计算出一个 杂凑 （获取任意大小数据并将其转换为固定长度值的函数）明文，然后使用其私钥对其进行签名。他们 通过应用解密中使用的相同公式对哈希签名 （m = cd 模式）。邮件签名后，他们会将此数字签名与邮件一起发送给收件人.

如果收件人收到带有数字签名的邮件，则可以使用 签名以检查邮件是否由声称已发送邮件的人的私钥真实签名. 他们还可以查看消息发送后，攻击者是否更改了该消息.

为了检查数字签名，收件人首先使用相同的哈希函数来查找他们收到的消息的哈希值。然后，收件人应用 发件人的公钥 到数字签名, 使用加密公式 （c =米Ë mod n）, 给他们数字签名的哈希值.

通过 比较从加密的数字签名中收到的消息的哈希值和哈希值, 收件人可以告诉邮件是否真实. 如果两个值相同，则消息自签名以来未更改 由原始发件人。如果消息甚至被更改为单个字符，则哈希值将完全不同.

RSA安全 & 攻击

像大多数密码系统一样，RSA的安全性取决于其实现和使用方式。一个重要因素是密钥的大小。的 密钥中的位数越多（基本上是密钥的长度），越难破解攻击 例如蛮力和保理.

由于可以通过整数分解来破坏诸如RSA之类的非对称密钥算法，而不能通过诸如AES之类的对称密钥算法来破坏RSA密钥，因此RSA密钥需要更长的时间才能达到相同的安全级别。.

目前， 已分解的最大密钥大小为768位长. 这是由一群学者在两年的时间内使用数百台机器完成的.

由于保理工作已于2009年底完成，并且自那时以来，计算能力已显着提高，因此可以假定尝试进行类似强度的尝试 现在可以考虑更大的RSA密钥.

尽管如此，这种攻击所需的时间和资源仍使它超出了大多数黑客的控制范围，无法进入民族国家的领域。最佳密钥长度取决于您的个人威胁模型。美国国家标准技术研究所 建议的最小密钥大小为 2048位, 但也使用4096位密钥 在某些情况下威胁级别较高.

分解只是RSA破解的一种方法。数量众多的其他攻击都有可能使用较少的资源破坏加密，但是这些取决于实施和其他因素，而不一定取决于RSA本身。其中一些包括：

素数真的是随机的吗?

RSA的某些实现使用弱随机数生成器得出质数。如果这些数字不是足够随机，则攻击者可以更轻松地分解它们并破坏加密。这个问题 使用密码安全的伪随机数生成器可以避免.

密钥生成不良

RSA密钥需要落入某些参数内才能使其安全. 如果素数 p 和 q 距离太近，很容易发现钥匙. 同样，数字 d 组成私钥的一部分不能太小. 低值使其易于解决。这些数字必须足够长，以确保您的钥匙安全，这一点很重要.

旁道攻击

这是一种不会直接破坏RSA的攻击，而是使用其实施中的信息为攻击者提供有关加密过程的提示。这些攻击可能包括 分析正在使用的电量, 要么 分支预测分析, 它使用执行时间度量来发现私钥.

另一种类型的侧信道攻击称为定时攻击。如果攻击者能够在目标计算机上针对许多不同的加密邮件测量解密时间, 该信息可以使攻击者确定目标的私钥.

RSA的大多数实现都通过在加密过程中添加一次性值来避免这种攻击，从而消除了这种相关性。这个过程叫做 密码盲.

RSA加密对未来安全吗？?

好消息是，尽管存在这些可能的攻击，但仍认为RSA使用安全。注意的是 需要正确实施并使用正确参数内的密钥. 正如我们刚刚讨论的那样，不使用填充，使用大小不足够的素数或存在其他漏洞的实施都不能被认为是安全的.

如果要使用RSA加密, 确保您使用的是至少1024位的密钥. 具有较高威胁模型的用户如果要放心使用RSA，则应坚持使用2048或4096位密钥。只要您意识到RSA的弱点并正确使用它，就应该可以安全地使用RSA进行密钥共享以及需要公钥加密的其他类似任务.

也可以看看： 常见的加密类型说明