
Diffie-Hellman密钥交换是 公钥密码学最重要的发展之一 并且仍然经常在当今各种不同的安全协议中实施.
它允许以前未见过的两个参与者安全地建立密钥,他们可以使用该密钥来保护其通信。在本文中,我们将解释其用途,逐步操作,其不同的变体以及为了安全实施而需要注意的安全注意事项.
什么是Diffie-Hellman密钥交换?
Diffie-Hellman密钥交换是 第一种广泛使用的在不安全通道上安全开发和交换密钥的方法.
在上述术语中,这似乎并不那么令人兴奋或具有突破性,所以让我们举一个例子来说明为什么Diffie-Hellman密钥交换是密码学领域如此重要的里程碑,以及为什么今天仍然如此频繁使用它.
假设您是最高机密的间谍,您需要向总部发送一些重要信息. 您将如何阻止您的敌人掌握信息?
最常见的解决方案是使用代码对消息进行加密。最简单的方法是预先安排您计划使用的任何类型的代码和密钥,或者通过安全的通信渠道进行处理.
假设您是个特别卑鄙的间谍,并且您和您的总部决定使用弱转换密码对邮件进行编码。在此代码中,每个“ a”都变为“ b”,每个“ b”都变为“ c”,每个“ c”都变为“ d”,依此类推,一直到“ z”都变为“ a”.
在此转换密码下,“让我们吃饭”的消息变为“ Mfu’t hfu ejoofs”。幸运的是,在我们的假设情况下,您的对手和您一样无能,并且无法破解这样一个简单的代码,这使他们无法访问消息的内容.
但是,如果您无法事先与收件人安排代码,会发生什么情况??
假设您想与一个从未见过盟友的间谍进行交流。您没有安全的渠道与他们交谈。如果您不加密消息,则任何拦截该消息的对手都可以阅读其中的内容。如果您在不告知盟友密码的情况下对其进行加密,那么敌人将无法读取它,但盟友也不会.
直到1970年代,这个问题一直是密码学最大的难题之一:
如果您没有机会提前共享密钥,如何与他人安全地交换信息?
Diffie-Hellman密钥交换是解决此问题的第一个公开使用的机制。该算法允许从未碰面的人安全地创建共享密钥,即使是在对手可能正在监视的不安全通道上.
Diffie-Hellman密钥交换的历史
Diffie-Hellman密钥交换的历史可以追溯到1970年代。在整个20世纪初期,密码学领域取得了显着发展,但这些进展主要集中在对称密钥密码学领域.
直到1976年,Whitfield Diffie和Martin Hellman发表论文后,公钥算法才在公共领域出现。, 密码学的新方向. 此次合作概述了新系统背后的机制,该新系统将被称为 Diffie-Hellman密钥交换.
该作品的部分灵感来自拉尔夫·默克尔(Ralph Merkle)的早期发展。所谓的 默克尔的谜题 涉及到一方创建并向另一方发送许多密码难题。这些难题将需要适度的计算资源来解决.
接收者会随机选择一个难题来解决,然后花费必要的精力来完成它. 解决难题后,就会向接收者显示标识符和会话密钥. 然后,接收者将标识符发送回原始发送者,让发送者知道已解决了哪个难题.
由于原始发件人创建了谜题,因此标识符可以使他们知道收件人发现了哪个会话密钥,并且双方可以使用此密钥进行更安全的通信。如果攻击者正在侦听交互,他们将可以访问所有谜题,以及接收者传输回原始发送者的标识符.
标识符不会告诉攻击者正在使用哪个会话密钥,因此解密信息的最佳方法是: 解决所有难题以找出正确的会话密钥. 由于攻击者平均必须解决一半的难题,因此最终导致他们发现密钥的难度比接收者要难得多.
这种方法提供了更高的安全性,但远非完美的解决方案。 Diffie-Hellman密钥交换采用了其中一些想法,并使它们变得更加复杂,从而创建了一种安全的公钥加密方法.
尽管它已被称为Diffie-Hellman密钥交换,但Martin Hellman提出将该算法命名为Diffie-Hellman-Merkle密钥交换,以反映Ralph Merkle对公共密钥密码学所做的工作.
公开认为,直到1997年英国政府解密1970年代初所做的工作时,默克尔,海尔曼和迪菲是最早开发公钥密码术的人。 詹姆斯·埃利斯,克利福德·考克斯和马尔科姆·威廉姆森.
事实证明,这三个人在1969年至1973年之间提出了第一个公钥加密方案,但他们的工作被分类了二十年。它是在英国情报机构政府通讯总部(GCHQ)下进行的.
他们的发现实际上是RSA算法,因此Diffie,Hellman和Merkle仍然是最早开发Diffie-Hellman密钥交换的人,但不再是第一个公开密钥密码学的发明者。.
Diffie-Hellman密钥交换在哪里使用?
Diffie-Hellman密钥交换的主要目的是 安全地开发可用于导出密钥的共享机密。然后可以将这些密钥与对称密钥算法一起使用,以受保护的方式传输信息. 对称算法往往用于加密大量数据,因为它们比公钥算法更有效.
从技术上讲,Diffie-Hellman密钥交换可用于建立公共和私有密钥。但是,实际上,往往倾向于使用RSA。这是因为RSA算法还能够签名公共密钥证书,而Diffie-Hellman密钥交换却不能够.
PGP中大量使用的ElGamal算法基于Diffie-Hellman密钥交换,因此使用该协议的任何协议都可以有效地实现一种Diffie-Hellman.
作为安全分配密钥的最常用方法之一,Diffie-Hellman密钥交换是 经常在TLS,IPsec,SSH,PGP等安全协议中实现. 这使其成为我们安全通信不可或缺的一部分.
作为这些协议的一部分,Diffie-Hellman密钥交换通常用于帮助保护您与网站的连接,远程访问另一台计算机以及发送加密的电子邮件。
Diffie-Hellman密钥交换如何工作?
Diffie-Hellman密钥交换非常复杂,可能很难掌握其工作原理. 它使用大量数字和大量数学, 我们许多人仍然从那些漫长而枯燥的高中课程中学到的东西.
使事情更容易理解, 我们将以一个类比来解释Diffie-Hellman密钥交换. 大致了解其工作原理后,我们将继续对基础流程进行更详细的技术描述.
Diffie-Hellman方案的最佳类比是考虑 两人混合涂料. 让我们使用加密标准,并说它们的名字是Alice和Bob. 他们俩都同意从随机颜色开始. 假设他们互相发送一条消息, 决定以黄色为常见颜色, 如下图所示:
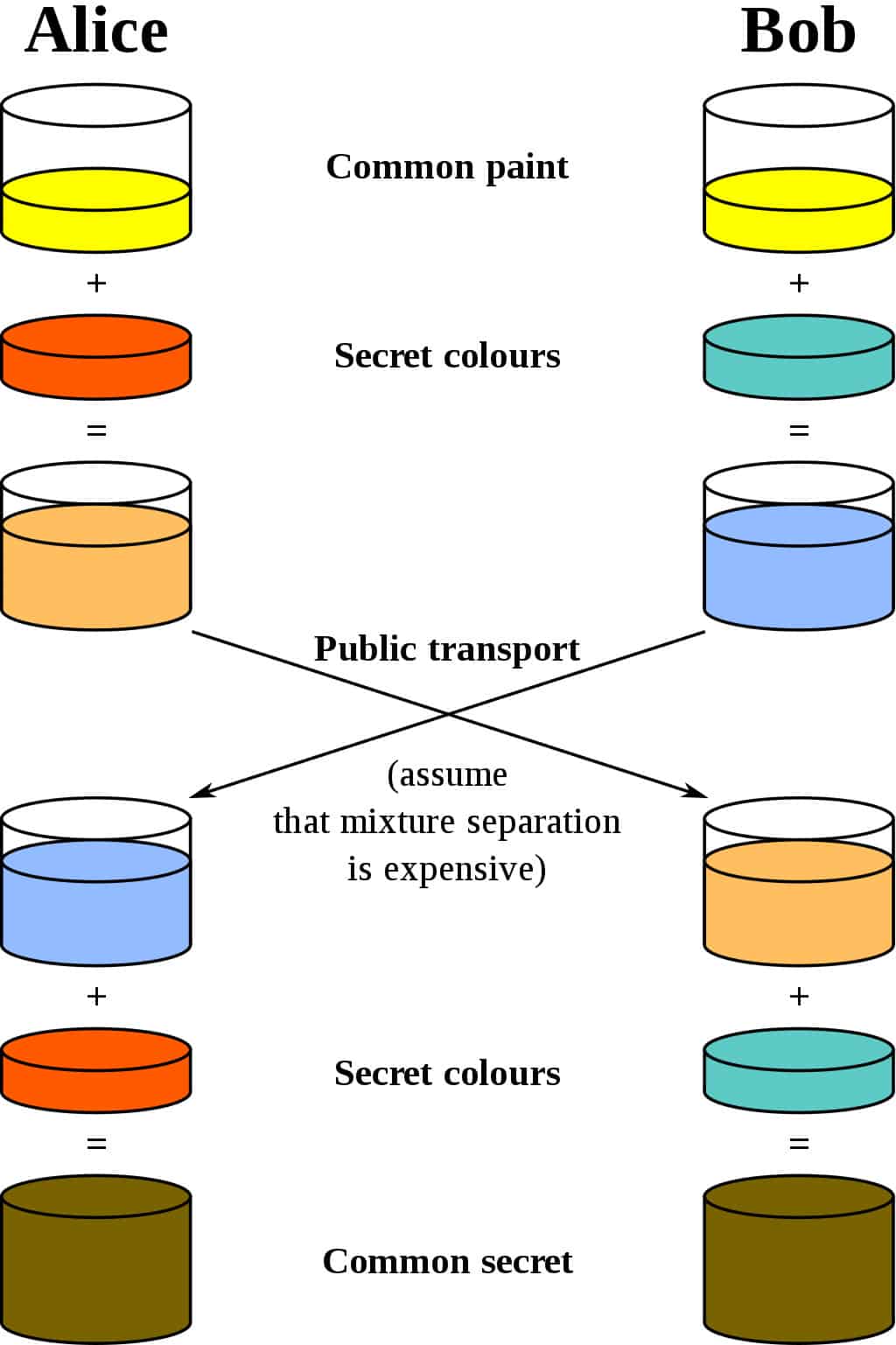
自己的秘密颜色。他们不告诉对方他们的选择。假设爱丽丝选择 红色, 而鲍勃选择一个 淡绿色的蓝色.
下一步是爱丽丝和鲍勃将他们的秘密颜色(爱丽丝为红色,鲍勃为蓝绿色)和双方共同同意的黄色混合在一起。根据该图,爱丽丝最终得到一个 橙混合, 而鲍勃的结果是 深蓝色.
完成混音后,将结果发送给另一方. 爱丽丝深蓝色, 而 鲍勃被送去了橙色油漆.
一旦收到合作伙伴的混合结果,他们就会在其中添加秘密颜色. 爱丽丝(Alice)接受更深的蓝色,并添加她的秘密红色颜料, 而 鲍勃将他秘密的蓝绿色添加到他刚收到的橙色混合物中.
结果? 他们都以相同的颜色出来, 在这种情况下是令人作呕的棕色。它可能不是您想要用来粉刷客厅的那种颜色,但是它仍然是一种共享的颜色。这种共享的颜色称为 共同的秘密.
Diffie-Hellman密钥交换的关键部分是,双方最终都将获得相同的结果,而无需跨通信通道发送整个公共秘密。. 选择一种共同的颜色,即自己的秘密颜色,交换混合色,然后再次添加自己的颜色,为双方提供了一种达成相同的共同秘密的方式,而无需传递整个内容.
如果攻击者正在侦听交换,则他们只能访问Alice和Bob开始使用的常见黄色以及交换的混合色。因为这实际上是用大量的而不是油漆完成的, 这些信息不足以使攻击者无法辨别最初的秘密颜色或常见秘密 (从技术上讲,可以从该信息计算出公共秘密,但是在Diffie-Hellman密钥交换的安全实现中,这样做将花费大量的时间和计算资源).
Diffie-Hellman密钥交换的这种结构使其非常有用. 它允许双方通过潜在的危险连接进行通信,并且仍然提出一个共享的机密,可以将其用作未来通信的加密密钥. 攻击者是否在监听都没关系,因为不会通过连接发送完整的共享机密.
Diffie-Hellman密钥交换的技术细节
是时候进行一些数学运算了……
不用担心,我们会慢慢进行,并尝试使整个过程尽可能容易理解。它遵循与上面显示的类比类似的前提,但是没有混合并发送颜色, Diffie-Hellman方案实际上是根据非常大的素数进行计算,然后将它们发送到.
为了确保安全,建议 主要 (p)至少2048位长, 这是大约等于此大小的十进制数字的二进制等效项:
415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019
为了防止任何人的头部爆炸,我们将以小得多的数字进行解释。意识到 如果Diffie-Hellman密钥交换使用的数字与我们示例中的数字一样小,它将是不安全的. 我们仅使用这么小的数字以更简单的方式演示该概念.
Diffie-Hellman密钥交换的最基本形式, 爱丽丝(Alice)和鲍勃(Bob)首先确定两个数字开头, 与上面示例中的单一普通涂料相反。这些是 模数(p)和基数(G).
实际使用中, 模数(p)是非常大的素数, 而 基地(G)相对较小,以简化计算. 基地(G)衍生自循环群(G)通常在其他步骤发生之前生成.
对于我们的示例,假设模数(p)是 17, 而基地(G)是 4.
一旦他们共同决定了这些号码,爱丽丝便会确定一个秘密号码(一种),而鲍勃则选择自己的秘密号码(b)。假设他们选择:
a = 3
b = 6
然后,爱丽丝执行以下计算,以提供她将发送给鲍勃的电话号码:
A = ga mod p
在上面的计算中, 模 表示取模运算。这些本质上是用来计算左侧除以右侧后的余数的计算。举个例子:
15 mod 4 = 3
如果您了解模运算的工作原理,则可以在以下计算中自行完成,否则可以使用在线计算器.
因此,让我们将数字放入公式中:
A = 43模组17
A = 64 mod 17
A = 13
当我们对Bob进行相同操作时,我们得到:
B = 46 mod 17
B = 4096 mod 17
B = 16
然后,爱丽丝发送她的结果(一种)给鲍勃,而鲍勃将他的身影(乙)给爱丽丝。然后,爱丽丝计算出共享机密(s)使用她从鲍勃(乙)和她的秘密号码(一种),使用以下公式:
s = Ba mod p
s = 163 mod 17
s = 4,096 mod 17
s = 16
然后,鲍勃执行了基本上相同的计算,但是使用了爱丽丝给他发送的号码(一种),以及他自己的秘密号码(b):
s = 一种b 模 p
s = 136 mod 17
s = 4,826,809 mod 17
s = 16
如您所见,双方最终获得了相同的结果 s, 16. 这是共享的秘密,只有爱丽丝和鲍勃知道。然后,他们可以使用它来为对称加密设置密钥,从而允许他们以只有他们可以访问的方式在彼此之间安全地发送信息。.
请注意,尽管 乙 和 s 与上面的示例相同,这只是基于为该示例选择的少量数字的巧合。通常,在Diffie-Hellman密钥交换的实际实现中,这些值将是不同的.
即使上述大部分数据都是以明文形式通过通道发送的(p,g,A 和 乙),并可由潜在的攻击者读取,共享的机密(s)从不传输。攻击者计算共享机密(s)或其中一个秘密号码(一种 和 b)以明文形式发送的信息.
当然,这假设Diffie-Hellman密钥交换已正确实施并且使用了足够大的数字。只要遵守这些规定,Diffie-Hellman密钥交换就被认为是建立共享秘密的安全方法,可用于保护未来的通信.
在多方之间建立共享密钥
Diffie-Hellman密钥交换还可以用于与更多参与者建立共享密钥。它的工作方式相同,不同之处在于各方需要进一步进行计算以添加其秘密号码并最终得到相同的共享秘密.
就像在Diffie-Hellman密钥交换的两方版本中一样,部分信息是通过不安全的通道发送的,但不足以使攻击者能够计算出共享密钥.
为什么Diffie-Hellman密钥交换是安全的?
在数学级别上,Diffie-Hellman密钥交换依赖于单向功能作为其安全性的基础。这些是一种简单的计算方法,但反之则困难得多.
更具体地说,它依赖于Diffie-Hellman问题,该问题假设在正确的参数下,计算不可行。 Gb 从…的单独值 G, G一种 和 Gb. 当前没有公开的方法可以轻松找到 Gb 不同于其他值,这就是为什么尽管攻击者可以截取值的事实,但仍将Diffie-Hellman密钥交换视为安全的原因 p, G, 一种, 和 乙.
认证方式 & Diffie-Hellman密钥交换
在现实世界中,很少使用Diffie-Hellman密钥交换。这背后的主要原因是 它不提供身份验证,使用户容易受到中间人攻击.
当Diffie-Hellman密钥交换本身实现时,会发生这些攻击,因为 它无法验证连接中的另一方是否真的是他们所说的真实身份. 没有任何形式的认证, 用户实际上可能正在与攻击者建立联系 当他们认为自己正在与可信赖的一方交流时.
因此,Diffie-Hellman密钥交换通常与某些身份验证方法一起实施。这通常涉及使用数字证书和公钥算法(例如RSA)来验证双方的身份.
Diffie-Hellman密钥交换的变体
Diffie-Hellman密钥交换可以以多种不同的方式实现,并且它还为其他几种算法提供了基础。其中一些实现提供授权,而另一些则具有各种加密功能,例如完美的前向保密性.
椭圆曲线Diffie-Hellman
椭圆曲线Diffie-Hellman利用椭圆曲线的代数结构,以使其实现以较小的密钥大小实现相似的安全级别。 224位椭圆曲线密钥提供的安全级别与2048位RSA密钥相同。这样可以提高交换效率并减少存储需求.
除了较小的密钥长度及其依赖于椭圆曲线的特性外,椭圆曲线Diffie-Hellman的操作方式与标准Diffie-Hellman密钥交换类似.
TLS
TLS是用于保护大部分Internet的协议,可以通过三种不同的方式使用Diffie-Hellman交换:匿名,静态和临时。实际上,仅应实施临时Diffie-Hellman,因为其他选项都存在安全问题.
- 匿名迪菲·赫尔曼 –此版本的Diffie-Hellman密钥交换不使用任何身份验证,因此很容易受到中间人攻击。不应使用或实现.
- 静态迪菲·赫尔曼 –静态Diffie-Hellman使用证书对服务器进行身份验证。默认情况下,它不对客户端进行身份验证,也不提供前向保密性.
- 短暂的迪菲·赫尔曼 –这被认为是最安全的实现,因为它提供了完美的前向保密性。通常将其与DSA或RSA之类的算法结合使用,以验证连接中的一方或双方。每次运行协议时,临时Diffie-Hellman都会使用不同的密钥对。这使连接具有完美的前向保密性,因为即使将来密钥被泄露,也无法将其用于解密所有过去的消息.
埃尔加马尔
ElGamal是建立在Diffie-Hellman密钥交换之上的公共密钥算法。与Diffie-Hellman一样,它本身不包含任何身份验证条款,并且通常为此目的与其他机制结合使用.
ElGamal主要用于PGP,GNU Privacy Guard和其他系统,因为其主要竞争对手RSA已获得专利。 RSA的专利于2000年到期,因此该日期之后可以免费实施。从那时起,ElGamal的实施频率就不再那么高.
STS
站到站(STS)协议也基于Diffie-Hellman密钥交换。这是另一个关键协议方案,但是它可以防止中间人攻击以及完善的前向保密性.
它要求连接双方都已经有一个密钥对,用于对双方进行身份验证。如果双方还不认识,则可以使用证书来验证双方的身份.
Diffie-Hellman密钥交换 & RSA
正如我们之前讨论的, Diffie-Hellman密钥交换通常与RSA或其他算法一起实现,以为连接提供身份验证. 如果您熟悉RSA,您可能会想知道 为什么还会有人麻烦使用Diffie-Hellman密钥交换, 由于RSA使以前从未见过的各方能够安全地进行通信.
RSA允许其用户使用其对应方的公钥对邮件进行加密,从而只能使用匹配的私钥对其进行解密。但是,实际上, RSA并不用于加密全部通信,这太低效了.
相反,RSA通常仅用作认证双方的手段。它这样做 双方的数字证书,这些数字证书将由证书颁发机构进行验证 证明证书所有者确实是他们所说的真实身份,并且证书上的公钥实际上属于他们.
用于相互认证, 各方将使用其私钥签名消息,然后将其发送给其通信伙伴. 然后每个收件人都可以 通过根据通信伙伴的数字证书上的公钥检查已签名的消息来验证另一方的身份 (请参阅上述有关RSA的文章,详细了解其工作原理,尤其是 签名消息 部分).
现在双方都已通过身份验证,从技术上讲,可以继续使用RSA安全地在彼此之间发送加密的消息,但是最终效率太低.
为了避免这种低效率,许多安全协议使用诸如 Diffie-Hellman密钥交换提出一个共同的秘密,可用于建立共享的对称密钥. 然后,将这种对称密钥用于对称密钥算法(例如AES)中以加密数据 双方打算在彼此之间安全发送.
这似乎是一个复杂而复杂的过程,但是与整个交换使用公共密钥算法相比,它最终对资源的需求更快,更少。这是因为 对称密钥加密比公共密钥加密效率高几个数量级.
除了我们刚才提到的低效率之外,仅使用RSA还会带来其他一些缺点. RSA需要填充以确保其安全性, 因此,需要在其旁边适当实施其他算法以使其安全.
RSA无法提供完美的前向保密性, 二者之一,与临时Diffie-Hellman密钥交换相比,这是另一个缺点。总而言之,这些原因就是为什么在许多情况下,最好仅将RSA与Diffie-Hellman密钥交换结合使用.
另外,Diffie-Hellman密钥交换可以与数字签名标准(DSS)之类的算法结合使用,以提供身份验证,密钥交换,机密性并检查数据的完整性。在这种情况下,无需使用RSA来确保连接安全.
Diffie-Hellman密钥交换的安全性问题
Diffie-Hellman密钥交换的安全性取决于其实现方式以及为其选择的编号。如上所述,它本身无法对另一方进行身份验证,但是在实践中,会使用其他机制来确保连接中的另一方不是冒名顶替者.
号码选择参数
如果Diffie-Hellman密钥交换的真实实现使用的数字与我们示例中的数字一样小,那么对于攻击者来说,交换过程将变得微不足道。但重要的不只是数字的大小-数字还需要足够随机。如果随机数生成器产生可预测的输出,则可能会完全破坏Diffie-Hellman密钥交换的安全性.
号码 p 应该是2048位长 确保安全. 基地, G, 可以是相对较小的数字,例如2, 但它必须来自 G 有很大的素数
Logjam攻击
Diffie-Hellman密钥交换是基于难以解决的离散对数问题设计的. 寻找解决方案的最有效的公知机制是数字字段筛选算法.
设计Diffie-Hellman密钥交换时已考虑到该算法的功能。到1992年,已知, G, 该算法涉及的四个步骤中的三个步骤可以预先计算。如果保存了此进度,则可以在相对较短的时间内计算出最终步骤.
直到意识到互联网流量的很大一部分都使用1024位或更小的相同组,这才引起关注。 2015年,一个学术团队对TLS中Diffie-Hellman密钥交换使用的最常见的512位素数进行了计算.
他们还能够将支持DHE-EXPORT的TLS服务器的80%降级,以便他们接受连接的512位出口级Diffie-Hellman密钥交换。这意味着 这些服务器中的每一个都容易受到资源丰富的对手的攻击.
研究人员继续推断他们的结果, 估计一个民族国家可能会破坏1024位素数. 通过打破单个最常用的1024位素数,学术团队估计,对手可以监视一百万个最受欢迎的HTTPS网站中的18%.
他们继续说,第二个主要因素将使对手能够解密66%的VPN服务器和26%的SSH服务器的连接。在报告的后面,学者们建议国家安全局可能已经具备了这些能力.
“仔细阅读已发布的NSA漏洞,可以发现该机构对VPN的攻击与这种突破是一致的。”
尽管存在此漏洞,但如果实施正确,Diffie-Hellman密钥交换仍然可以保持安全。只要使用2048位密钥,Logjam攻击就不会起作用。更新的浏览器也可以抵御这种攻击.
Diffie-Hellman密钥交换安全吗??
尽管Diffie-Hellman密钥交换看似复杂,但它是安全地在线交换数据的基础部分。只要与适当的身份验证方法一起实施并且正确选择了编号,就不会认为它容易受到攻击.
Diffie-Hellman密钥交换是一种创新的方法,可以帮助两个未知方在1970年代开发安全地进行通信。虽然我们现在使用更大的密钥实施更新版本以防止现代技术 该协议本身看起来将一直保持安全性,直到量子计算的到来 以及随之而来的高级攻击.
网络安全业务技术 由TheDigitalArtist根据 CC0