
Diffie-Hellmanキー交換は 公開鍵暗号方式の最も重要な開発の1つ そして、今日のさまざまなセキュリティプロトコルの範囲でまだ頻繁に実装されています.
これにより、以前に会ったことがない2人の当事者が、通信を保護するために使用できるキーを安全に確立できます。この記事では、その用途、ステップごとの動作、さまざまなバリエーション、および安全に実装するために注意する必要があるセキュリティの考慮事項について説明します.
Diffie-Hellman鍵交換とは?
Diffie-Hellmanキー交換は 安全でないチャネルを介して安全にキーを開発および交換する最初の広く使用されている方法.
上記の用語ではそれほどエキサイティングでも画期的でもないように思えるので、Diffie-Hellman鍵交換が暗号化の世界で非常に重要なマイルストーンだった理由と、今日でも頻繁に使用されている理由を説明してみましょう。.
あなたが最高機密のスパイであり、本部にいくつかの重要な情報を送信する必要があるとしましょう. 敵がメッセージを手に入れるのをどのように防ぎますか?
最も一般的な解決策は、コードを使用してメッセージを暗号化することです。最も簡単な方法は、事前に使用する予定のコードとキーのタイプを事前に準備するか、安全な通信チャネルで行うことです。.
あなたが特に悪意のあるスパイであり、あなたとあなたの本社が弱いシフト暗号を使用してメッセージをエンコードすることにしたとしましょう。このコードでは、すべての「a」が「b」になり、すべての「b」が「c」になり、すべての「c」が「d」になり、「z」が「a」になるまで続きます。.
このシフト暗号では、「Let’s get dinner」というメッセージが「Mfu’t hfu ejoofs」になります。ありがたいことに、私たちの仮想的な状況では、あなたの敵はあなたと同じように無能であり、そのような単純なコードを解読することができず、メッセージの内容にアクセスできなくなります.
ただし、事前に受信者とコードを調整できなかった場合はどうなりますか?
あなたが今まで会ったことがない同盟国からのスパイと通信したいとしましょう。彼らと話すための安全なチャンネルがありません。メッセージを暗号化しない場合、メッセージを傍受する敵は内容を読むことができます。コードを味方に伝えずに暗号化すると、敵はそれを読むことができなくなりますが、味方も.
この問題は、1970年代までの暗号化における最大の難問の1つでした。
事前に鍵を共有する機会がなかった場合、どうすれば誰かと安全に情報を交換できますか?
Diffie-Hellman鍵交換は、この問題を解決するための最初の公的に使用されたメカニズムでした。このアルゴリズムにより、これまでに会ったことのない人でも、攻撃者が監視している可能性のある安全でないチャネルを介して共有キーを安全に作成できます。.
Diffie-Hellman鍵交換の歴史
Diffie-Hellman鍵交換は、そのルーツを1970年代までさかのぼります。暗号化の分野は20世紀前半を通じて著しく発展しましたが、これらの進歩は主に対称鍵暗号化の分野に焦点を当てていました.
Whitfield DiffieとMartin Hellmanが論文を発表したとき、公開鍵アルゴリズムが公開されたのは1976年までではありませんでした, 暗号の新しい方向. コラボレーションでは、新しいシステムの背後にあるメカニズムの概要を説明しました。 Diffie-Hellman鍵交換.
この作品は、ラルフ・マークルによって行われた以前の開発に一部影響を受けました。いわゆる マークルのパズル ある当事者がいくつかの暗号パズルを作成し、他の当事者に送信することを含みます。これらのパズルは、解くのに適度な量の計算リソースを必要とします.
受信者は、解決するパズルを1つランダムに選択し、それを完了するために必要な努力を費やします. パズルが解決されると、識別子とセッションキーが受信者に公開されます. その後、受信者は元の送信者に識別子を送り返し、送信者はどのパズルが解決されたかを知ることができます.
元の送信者がパズルを作成したため、識別子によって受信者がどのセッションキーを発見したかがわかり、2者はこのキーを使用してより安全に通信できます。攻撃者がインタラクションを傍受している場合、攻撃者はすべてのパズルと、受信者が元の送信者に送信する識別子にアクセスできます。.
識別子は、どのセッションキーが使用されているかを攻撃者に伝えないため、情報を解読するための最良のアプローチは すべてのパズルを解いて正しいセッションキーを発見する. 攻撃者は平均してパズルの半分を解かなければならないので、受信者よりも鍵を明らかにするのがはるかに困難になります.
このアプローチはより多くのセキュリティを提供しますが、完璧なソリューションにはほど遠いです。 Diffie-Hellman鍵交換は、これらのアイデアのいくつかを取り入れ、公開鍵暗号化の安全な方法を作成するために、より複雑にしました。.
Diffie-Hellman鍵交換として知られるようになりましたが、Martin Hellmanは、Ralph Merkleが公開鍵暗号化に向けた作業を反映するために、アルゴリズムをDiffie-Hellman-Merkle鍵交換と呼ぶことを提案しました.
マークル、ヘルマン、ディフィーが公開鍵暗号を開発した最初の人々は1997年までだと公に考えられていました。 ジェームズ・エリス、クリフォード・コックス、マルコム・ウィリアムソン.
このトリオは、1969年から1973年の間に最初の公開鍵暗号化方式を考案しましたが、その作業は20年間分類されていました。英国のintelligence報機関である政府通信本部(GCHQ)の下で実施されました.
彼らの発見は実際にはRSAアルゴリズムであったため、Diffie、Hellman、Merkleは、Diffie-Hellman鍵交換を開発した最初の人物でしたが、公開鍵暗号の最初の発明者ではありませんでした.
Diffie-Hellmanキー交換はどこで使用されますか?
Diffie-Hellman鍵交換の主な目的は 鍵の導出に使用できる共有秘密を安全に開発します。これらのキーは、対称キーアルゴリズムと共に使用して、保護された方法で情報を送信できます。. 対称アルゴリズムは、公開鍵アルゴリズムよりも効率的であるため、データの大部分を暗号化するために使用される傾向があります.
技術的には、Diffie-Hellman鍵交換を使用して、公開鍵と秘密鍵を確立できます。ただし、実際には、代わりにRSAが使用される傾向があります。これは、RSAアルゴリズムも公開鍵証明書に署名できるのに対し、Diffie-Hellman鍵交換はできないためです。.
PGPで頻繁に使用されていたElGamalアルゴリズムはDiffie-Hellman鍵交換に基づいているため、それを使用するプロトコルはいずれも一種のDiffie-Hellmanを効果的に実装しています。.
キーを安全に配布するための最も一般的な方法の1つとして、Diffie-Hellmanキー交換は TLS、IPsec、SSH、PGPなどのセキュリティプロトコルで頻繁に実装されています. これは私たちの安全なコミュニケーションの不可欠な部分になります.
これらのプロトコルの一部として、Diffie-Hellman鍵交換は多くの場合、Webサイトへの接続の保護、別のコンピューターへのリモートアクセス、暗号化された電子メールの送信に使用されます。
Diffie-Hellman鍵交換の仕組み?
Diffie-Hellman鍵交換は複雑であり、その仕組みを理解するのが難しい場合があります. 非常に大きな数と多くの数学を使用します, 長くて退屈な高校の授業で私たちの多くがまだ恐れていること.
物事を少しわかりやすくするために, Diffie-Hellman鍵交換について類推して説明することから始めます. それがどのように機能するかの全体像をつかめば、基礎となるプロセスのより技術的な説明に移ります.
Diffie-Hellmanスキームの最良の例えは、 塗料を混合する二人. 暗号化標準を使用して、名前がアリスとボブだとしましょう. 彼らは両方ともで始まるランダムな色に同意する. 彼らがお互いにメッセージを送信し、 共通の色として黄色を決める, 下の図のように:
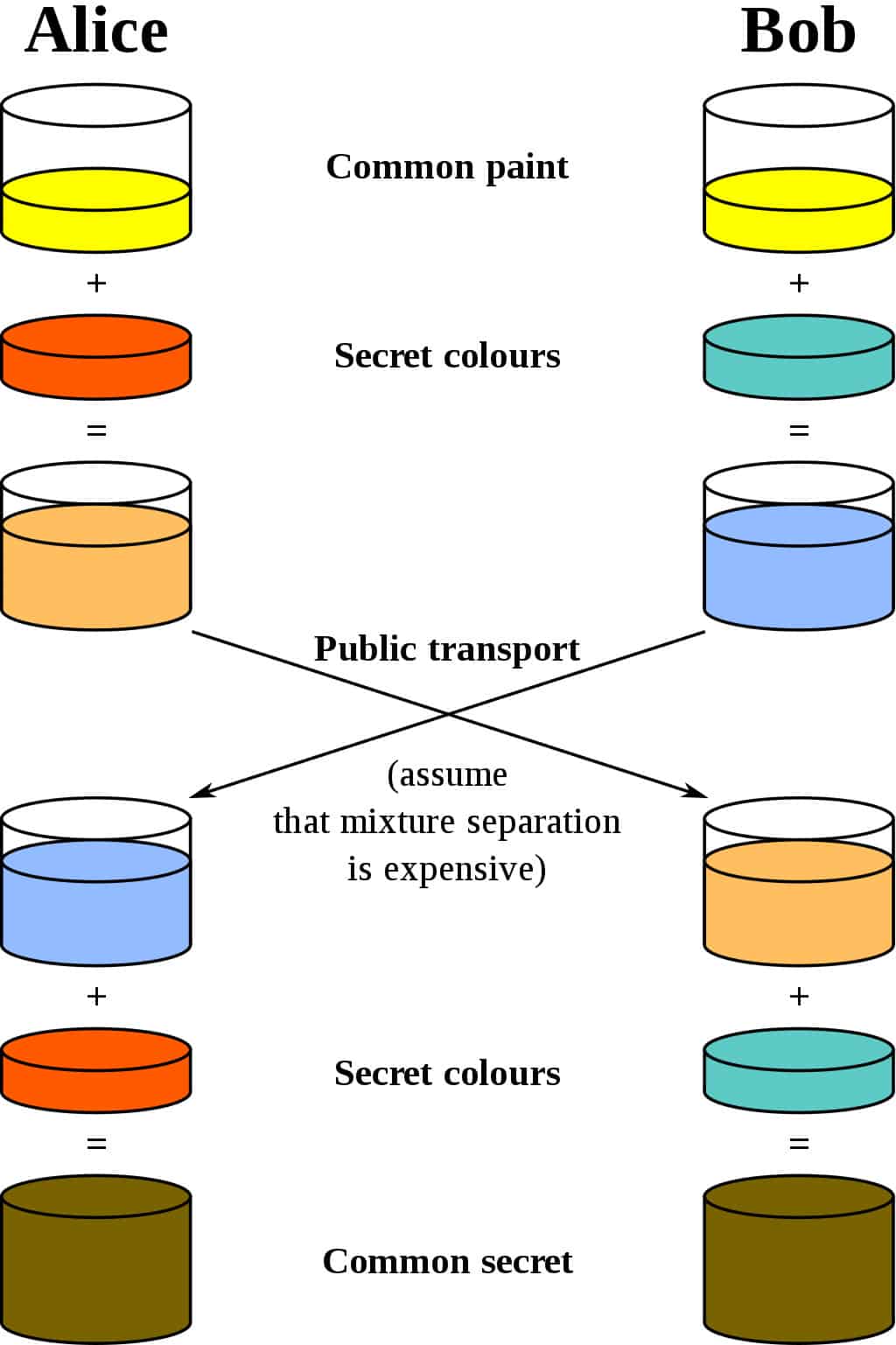
独自の秘密の色。彼らは彼らの選択を相手に伝えません。アリスが選んだとしましょう 赤, ボブが わずかに緑がかった青.
次のステップでは、アリスとボブの両方が、彼らの秘密の色(アリスの場合は赤、ボブの場合は緑がかった青)を互いに合意した黄色と混ぜます。図によると、アリスは最終的に オレンジ色のミックス, ボブの結果は より深い青.
ミキシングが完了すると、結果を相手に送信します. アリスはより深い青を受け取ります, ながら ボブはオレンジ色の塗料を送られます.
パートナーから混合結果を受け取ったら、彼らに秘密の色を追加します. アリスはより深い青を取り、彼女の秘密の赤いペンキを追加します, ながら ボブは受け取ったオレンジ色のミックスに秘密の緑がかった青を追加します.
結果? 両方とも同じ色で出てきます, この場合、それは嫌な茶色です。リビングルームをペイントしたいような色ではないかもしれませんが、それでも共有色です。この共有色はと呼ばれます 共通の秘密.
Diffie-Hellman鍵交換の重要な部分は、通信チャネルを介して共通の秘密全体を送信する必要なく、両方の当事者が同じ結果になることです。. 共通の色、独自の秘密の色を選択し、ミックスを交換してから独自の色をもう一度追加すると、両方の当事者が全体を送信することなく同じ共通の秘密に到達する方法が得られます.
攻撃者が交換を聞いている場合、アクセスできるのは、アリスとボブが最初から共通の黄色であり、交換される混合色です。これはペイントの代わりに膨大な数で本当に行われるので, これらの情報は、攻撃が初期の秘密の色または共通の秘密のいずれかを識別するのに十分ではありません (技術的には、この情報から共通の秘密を計算することは可能ですが、Diffie-Hellman鍵交換の安全な実装では、そうするには実行不可能な時間と計算リソースが必要になります).
Diffie-Hellman鍵交換のこの構造は、非常に有用なものです. これにより、2つのパーティは潜在的に危険な接続を介して通信できますが、将来の通信用の暗号化キーを作成するために使用できる共有シークレットを引き続き作成できます。. 完全な共有シークレットが接続経由で送信されることはないため、攻撃者がリッスンしていても問題ありません.
Diffie-Hellman鍵交換の技術的な詳細
数学の時間…
心配する必要はありません。処理を遅くし、プロセス全体をできるだけわかりやすくするようにします。上記のアナロジーと同様の前提に従いますが、色を混合して送信する代わりに, Diffie-Hellmanスキームは、実際には非常に大きな素数に基づいて計算を行い、それらを送信します.
セキュリティを確保するために、 プライム(p)少なくとも2048ビット長, これは、このサイズ程度の10進数に相当するバイナリです。
415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019
誰かの頭が爆発するのを防ぐために、この説明をより小さな数字で実行します。を注意 Diffie-Hellman鍵交換は、この例のような小さな数字を使用すると安全ではなくなります. このような小さな数字のみを使用して、より簡単な方法でコンセプトを示しています.
Diffie-Hellman鍵交換の最も基本的な形式, アリスとボブは、開始する2つの番号を相互に決定することから始めます, 上記の例の単一の一般的なペイントとは対照的です。これらは モジュラス(p)およびベース(g).
実用化中, モジュラス(p)は非常に大きな素数です, ながら 本拠 (g)計算を簡素化するために比較的小さい. 本拠 (g)は、巡回グループ(G)通常、他のステップが実行されるかなり前に生成されます.
この例では、モジュラス(p)は 17, 一方、ベース(g)は 4.
これらの番号を相互に決定すると、アリスは秘密の番号(a)ボブは自分の秘密番号を選択しますが(b)。彼らが選択したとしましょう:
a = 3
b = 6
次に、アリスは次の計算を実行して、ボブに送信する番号を提供します。
A = ga mod p
上記の計算で, モッド モジュロ演算を意味します。これらは基本的に、左側を右側で除算した後の残りを計算するための計算です。例として:
15 mod 4 = 3
モジュロ演算の仕組みを理解している場合は、次の計算で自分で行うことができます。それ以外の場合は、オンライン計算機を使用できます.
数式に数値を入れましょう:
A = 43 mod 17
A = 64 mod 17
A = 13
Bobに対して同じことを行うと、次のようになります。
B = 46 mod 17
B = 4096 mod 17
B = 16
アリスは結果を送信します(A)ボブに、ボブは彼の姿(B)アリスへ。次に、アリスは共有シークレット(s)彼女がボブから受け取った番号を使用して(B)と彼女の秘密の番号(a)、次の式を使用します。
s = Ba mod p
s = 163 mod 17
s = 4,096 mod 17
s = 16
その後、ボブは基本的に同じ計算を実行しますが、アリスが彼に送信した番号(A)、および彼自身の秘密番号(b):
s = Ab モッド p
s = 136 mod 17
s = 4,826,809 mod 17
s = 16
ご覧のとおり、両者は同じ結果になりました s, 16. これは、アリスとボブだけが知っている共有秘密です。次に、これを使用して対称暗号化のキーを設定し、自分だけがアクセスできる方法で安全に情報を送信できるようにします。.
ただし、 B そして s 上記の例では同じですが、これはこの図で選択された小さな数字に基づいた単なる偶然です。通常、これらの値はDiffie-Hellman鍵交換の実際の実装では同じではありません.
上記のデータの多くは平文でチャネルを介して送信されますが(p、g、A そして B)潜在的な攻撃者が読み取ることができる共有シークレット(s)は送信されません。攻撃者が共有秘密を計算することは実用的ではありません(s)またはいずれかの秘密番号(a そして b)平文で送信される情報から.
もちろん、これはDiffie-Hellman鍵交換が適切に実装され、十分に大きな数が使用されることを前提としています。これらの規定が守られている限り、Diffie-Hellman鍵交換は、将来の通信を保護するために使用できる共有秘密を確立する安全な方法と見なされます.
複数のパーティ間で共有キーを確立する
Diffie-Hellmanキー交換を使用して、より多くの参加者と共有キーをセットアップすることもできます。同じように機能しますが、各当事者が秘密番号を追加して同じ共有秘密を取得するためにさらにラウンドの計算が必要になることを除きます.
Diffie-Hellman鍵交換の2パーティバージョンと同様に、情報の一部は安全でないチャネルを介して送信されますが、攻撃者が共有シークレットを計算するには不十分です.
Diffie-Hellman鍵交換が安全な理由?
数学的レベルでは、Diffie-Hellmanキー交換は、セキュリティの基礎として一方向の機能に依存しています。これらは、一方向に実行するのは簡単ですが、逆に計算するのははるかに難しい計算です.
具体的には、Diffie-Hellman問題に依存しています。Diffie-Hellman問題では、適切なパラメータでは計算が不可能であると仮定しています。 gab の個別の値から g, ga そして gb. 現在、簡単に見つけるための公に知られている方法はありません gab 攻撃者が値を傍受できるにもかかわらず、Diffie-Hellmanキー交換は安全であると考えられる理由です。 p, g, A, そして B.
認証 & Diffie-Hellman鍵交換
現実の世界では、Diffie-Hellmanキー交換が単独で使用されることはほとんどありません。この背後にある主な理由は 認証を提供しないため、ユーザーが中間者攻撃に対して脆弱になります。.
これらの攻撃は、Diffie-Hellmanキー交換が単独で実装されている場合に発生する可能性があります。 接続の相手が本当に自分が言っているのかどうかを確認する手段がありません。. 認証の形式なし, ユーザーは実際に攻撃者と接続している可能性があります 信頼できる相手と通信していると思うとき.
このため、一般にDiffie-Hellman鍵交換は認証のいくつかの手段とともに実装されます。これには、多くの場合、デジタル証明書とRSAなどの公開鍵アルゴリズムを使用して、各当事者の身元を確認することが含まれます.
Diffie-Hellman鍵交換のバリエーション
Diffie-Hellman鍵交換は、さまざまな方法で実装できます。また、他のいくつかのアルゴリズムの基礎も提供しています。これらの実装には承認を提供するものもあれば、完全転送秘密などのさまざまな暗号化機能を備えているものもあります。.
楕円曲線Diffie-Hellman
楕円曲線Diffie-Hellmanは、楕円曲線の代数構造を利用して、その実装がより小さなキーサイズで同様のレベルのセキュリティを実現できるようにします。 224ビットの楕円曲線キーは、2048ビットのRSAキーと同じレベルのセキュリティを提供します。これにより、交換がより効率的になり、ストレージ要件が削減されます。.
鍵の長さが短いことと、楕円曲線の特性に依存しているという事実を除けば、楕円曲線Diffie-Hellmanは標準のDiffie-Hellman鍵交換と同様の方法で動作します.
TLS
インターネットの大部分を保護するために使用されるプロトコルであるTLSは、3つの異なる方法でDiffie-Hellman交換を使用できます。匿名、静的、および一時的です。実際には、一時的なDiffie-Hellmanのみを実装する必要があります。他のオプションにはセキュリティ上の問題があるためです。.
- 匿名のディフィー・ヘルマン –このバージョンのDiffie-Hellman鍵交換は認証を使用しないため、中間者攻撃に対して脆弱です。使用または実装しないでください.
- 静的ディフィーヘルマン – Static Diffie-Hellmanは、証明書を使用してサーバーを認証します。デフォルトではクライアントを認証せず、前方秘匿性も提供しません.
- エフェメラルディフィーヘルマン –これは、完全な前方秘匿性を提供するため、最も安全な実装と見なされます。通常、DSAやRSAなどのアルゴリズムと組み合わせて、接続の一方または両方を認証します。 Ephemeral Diffie-Hellmanは、プロトコルが実行されるたびに異なるキーペアを使用します。これにより、接続に完全な前方秘匿性が与えられます。これは、将来キーが危険にさらされても、過去のすべてのメッセージを解読するために使用できないためです。.
エルガマル
ElGamalは、Diffie-Hellman鍵交換の上に構築された公開鍵アルゴリズムです。 Diffie-Hellmanのように、それ自体には認証の規定が含まれておらず、一般にこの目的のために他のメカニズムと組み合わされています.
ElGamalは、主なライバルであるRSAが特許を取得しているため、主にPGP、GNU Privacy Guardおよびその他のシステムで使用されました。 RSAの特許は2000年に失効し、その日以降は自由に実装できるようになりました。それ以来、ElGamalはそれほど頻繁に実装されていません.
STS
ステーション間(STS)プロトコルもDiffie-Hellman鍵交換に基づいています。これは別の重要な合意スキームですが、man-in-the-middle攻撃からの保護と完全な秘密保持を提供します.
接続の両方の当事者が、各側の認証に使用されるキーペアをすでに持っている必要があります。当事者同士がまだ知られていない場合は、証明書を使用して両方の当事者の身元を検証できます.
Diffie-Hellman鍵交換 & RSA
前に説明したように, Diffie-Hellman鍵交換は、多くの場合、接続に認証を提供するためにRSAまたは他のアルゴリズムとともに実装されます。. RSAに精通している場合は、疑問に思うかもしれません なぜだれもがDiffie-Hellman鍵交換の使用も気にする理由, RSAは、これまでに会ったことのない関係者が安全に通信できるようにするため.
RSAを使用すると、ユーザーは対応する公開キーでメッセージを暗号化できるため、一致する秘密キーによってのみ解読できます。ただし、実際には, RSAは通信全体の暗号化には使用されません。これは非常に非効率的です.
代わりに、多くの場合、RSAは両方の当事者を認証する手段としてのみ使用されます。これで 認証局によって検証された各当事者のデジタル証明書 証明書の所有者が本人であることを証明し、証明書の公開鍵が実際に所有者であることを証明する.
相互認証の場合, 各当事者は、秘密鍵を使用してメッセージに署名し、通信パートナーに送信します. その後、各受信者は 通信相手のデジタル証明書の公開鍵と署名されたメッセージを照合して、相手の身元を確認します (これがどのように機能するかの詳細については、RSAに関する上記の記事を参照してください。 メッセージに署名する セクション).
両者が認証されたので、RSAを使用して暗号化されたメッセージを安全に送信することは技術的には可能ですが、効率が悪くなります.
この非効率性を回避するために、多くのセキュリティプロトコルは次のようなアルゴリズムを使用しています。 Diffie-Hellman鍵交換により、共有対称鍵を確立するために使用できる共通の秘密を見つけ出す. この対称キーは、AESなどの対称キーアルゴリズムで使用され、データを暗号化します。 両者が自分たちの間で安全に送信するつもりであること.
複雑で複雑なプロセスのように思えるかもしれませんが、交換全体に公開鍵アルゴリズムを使用する場合と比較すると、リソースに対する要求ははるかに高速で要求が少なくなります。それの訳は 対称キー暗号化は、公開キー暗号化よりも桁違いに効率的です.
先ほど述べた非効率性に加えて、RSAを単独で使用することから生じる他の欠点もいくつかあります。. RSAは安全にするためにパディングが必要です, したがって、安全にするために、追加のアルゴリズムを適切に実装する必要があります.
RSAは完全な秘密を提供しません, どちらも、一時的なDiffie-Hellman鍵交換と比較した場合の別の欠点です。まとめると、これらの理由が、多くの状況で、Diffie-Hellman鍵交換と併せてRSAのみを適用することが最善である理由です。.
あるいは、Diffie-Hellman鍵交換をデジタル署名標準(DSS)などのアルゴリズムと組み合わせて、認証、鍵交換、機密性を提供し、データの整合性をチェックすることができます。このような状況では、接続を保護するためにRSAは必要ありません.
Diffie-Hellman鍵交換のセキュリティ問題
Diffie-Hellmanキー交換のセキュリティは、それがどのように実装されているか、およびそのために選択された数に依存します。上で述べたように、それ自体で相手を認証する手段はありませんが、実際には、接続中の相手がなりすましでないことを保証するために他のメカニズムが使用されます.
番号選択のパラメーター
Diffie-Hellman鍵交換の実世界の実装で、この例の番号ほど小さい番号を使用した場合、攻撃者が解読プロセスを簡単に解読できるようになります。しかし、重要なのは数字のサイズだけではありません。数字も十分にランダムである必要があります。乱数ジェネレーターが予測可能な出力を生成する場合、Diffie-Hellman鍵交換のセキュリティを完全に損なう可能性があります.
人数、個数、総数 p 2048ビット長にする必要があります セキュリティを確保するために. 本拠, g, 2のような比較的小さな数にすることができます, しかし、それはの順序から来る必要があります G 大きな素因数がある
Logjam攻撃
Diffie-Hellman鍵交換は、解決が難しい離散対数問題に基づいて設計されました. 解決策を見つけるための最も効果的な公に知られているメカニズムは、数値フィールドふるいアルゴリズムです.
Diffie-Hellmanキー交換の設計時に、このアルゴリズムの機能が考慮されました。 1992年までに、特定のグループに対して, G, アルゴリズムに含まれる4つのステップのうち3つは、事前に計算される可能性があります。この進捗状況が保存されていれば、最終ステップは比較的短時間で計算できます.
インターネットトラフィックの大部分が1024ビット以下の同じグループを使用していることに気付くまで、これはあまり心配ではありませんでした。 2015年、学術チームがTLSのDiffie-Hellman鍵交換で使用される最も一般的な512ビットプライムの計算を実行しました.
また、DHE-EXPORTをサポートするTLSサーバーの80%をダウングレードできたため、512ビットのエクスポートグレードのDiffie-Hellman鍵交換を接続に受け入れました。この意味は これらの各サーバーは、リソースの豊富な敵からの攻撃に対して脆弱です。.
研究者は結果を推定し続けました, 国民国家が1024ビット素数を破ることができると推定する. 最も一般的に使用される単一の1024ビットプライムを壊すことにより、アカデミックチームは、100万の最も人気のあるHTTPS Webサイトの18%を敵が監視できると推定しました.
彼らはさらに、2番目の素数により、敵対者は66%のVPNサーバーと26%のSSHサーバーの接続を解読できると言いました。レポートの後半で、学者は、NSAがこれらの機能を既に持っている可能性があることを示唆しました.
「公開されたNSAリークの詳細を読むと、代理店のVPNへの攻撃は、そのような中断を達成したことと一致していることがわかります。」
この脆弱性にもかかわらず、Diffie-Hellmanキー交換は、正しく実装されていれば安全です。 2048ビットキーが使用されている限り、Logjam攻撃は機能しません。更新されたブラウザもこの攻撃から保護されています.
Diffie-Hellman鍵交換は安全ですか?
Diffie-Hellman鍵交換は複雑に見えるかもしれませんが、オンラインで安全にデータを交換するための基本的な部分です。適切な認証方法と一緒に実装され、番号が適切に選択されている限り、攻撃に対して脆弱であるとは見なされません。.
Diffie-Hellmanキー交換は、1970年代に開発された2つの未知の当事者が安全に通信できるようにするための革新的な方法でした。現在、最新のテクノロジーから保護するために、より大きなキーを備えた新しいバージョンを実装しています プロトコル自体は、量子コンピューティングの到来まで安全であり続けるように見えます それに伴う高度な攻撃.
サイバーセキュリティビジネステクノロジー TheDigitalArtistによるライセンス CC0