Cos’è lo scambio di chiavi Diffie-Hellman e come funziona?

Lo scambio di chiavi Diffie-Hellman fu uno degli sviluppi più importanti nella crittografia a chiave pubblica ed è ancora spesso implementato in una gamma di protocolli di sicurezza diversi di oggi.

Consente a due parti che non si sono mai incontrate in precedenza di stabilire in modo sicuro una chiave che possono utilizzare per proteggere le loro comunicazioni. In questo articolo, spiegheremo a cosa serve, come funziona passo per passo, le sue diverse varianti, nonché le considerazioni sulla sicurezza che devono essere annotate per implementarlo in sicurezza.

Qual è lo scambio di chiavi Diffie-Hellman?

Lo scambio di chiavi Diffie-Hellman fu il primo metodo ampiamente utilizzato per sviluppare e scambiare chiavi in ​​modo sicuro su un canale non sicuro.

Potrebbe non sembrare così eccitante o rivoluzionario nei termini di cui sopra, quindi diamo un esempio che spiega perché lo scambio di chiavi Diffie-Hellman è stato una pietra miliare così importante nel mondo della crittografia e perché è ancora così frequentemente usato oggi.

Supponiamo che tu sia una spia top secret e che devi inviare alcune informazioni importanti al tuo quartier generale. Come impediresti ai tuoi nemici di ottenere il messaggio?

La soluzione più comune sarebbe quella di crittografare il messaggio con un codice. Il modo più semplice è predisporre qualsiasi tipo di codice e chiave che prevedi di utilizzare in precedenza, oppure farlo tramite un canale di comunicazione sicuro.

Supponiamo che tu sia una spia particolarmente cattiva e tu e il tuo quartier generale decidiate di utilizzare un codice a turni debole per codificare i vostri messaggi. In questo codice, ogni “a” diventa “b”, ogni “b” diventa “c”, ogni “c” diventa “d”, e così via, fino alla “z” che diventa una “a”.

Con questo codice a turni, il messaggio “Andiamo a cena” diventa “Mfu’hfu ejoofs”. Per fortuna, nella nostra ipotetica situazione, i tuoi avversari sono incompetenti quanto te e non sono in grado di decifrare un codice così semplice, che impedisce loro di accedere ai contenuti del messaggio.

Ma cosa succede se non riesci a organizzare in anticipo un codice con il tuo destinatario?

Diciamo che vuoi comunicare con una spia di una nazione alleata che non hai mai incontrato prima. Non hai un canale sicuro su cui parlare con loro. Se non crittografare il tuo messaggio, qualsiasi avversario che lo intercetta sarà in grado di leggere i contenuti. Se lo crittografate senza dire al codice l’alleato, il nemico non sarà in grado di leggerlo, ma nemmeno l’alleato.

Questo problema era uno dei maggiori enigmi della crittografia fino agli anni ’70:

Come puoi scambiare informazioni in modo sicuro con qualcuno se non hai avuto l’opportunità di condividere la chiave in anticipo?

Lo scambio di chiavi Diffie-Hellman è stato il primo meccanismo usato pubblicamente per risolvere questo problema. L’algoritmo consente a coloro che non si sono mai incontrati prima di creare in modo sicuro una chiave condivisa, anche su un canale insicuro che gli avversari potrebbero monitorare.

La storia dello scambio di chiavi Diffie-Hellman

Lo scambio di chiavi Diffie-Hellman affonda le sue radici negli anni ’70. Mentre il campo della crittografia si era sviluppato in modo significativo durante i primi anni del XX secolo, questi progressi si concentravano principalmente nell’area della crittografia a chiave simmetrica.

Fu solo nel 1976 che emersero algoritmi a chiave pubblica nella sfera pubblica, quando Whitfield Diffie e Martin Hellman pubblicarono il loro articolo, Nuove direzioni nella crittografia. La collaborazione ha delineato i meccanismi alla base di un nuovo sistema, che sarebbe diventato noto come Scambio di chiavi Diffie-Hellman.

Il lavoro è stato in parte ispirato dai precedenti sviluppi realizzati da Ralph Merkle. Il cosidetto I puzzle di Merkle coinvolgere una parte nella creazione e nell’invio di un numero di enigmi crittografici all’altra. Questi enigmi richiederebbero una moderata quantità di risorse computazionali per risolvere.

Il destinatario sceglierebbe a caso un puzzle da risolvere e quindi spenderà lo sforzo necessario per completarlo. Una volta risolto il puzzle, un identificatore e una chiave di sessione vengono rivelati al destinatario. Il destinatario quindi trasmette l’identificatore al mittente originale, il che fa sapere al mittente quale puzzle è stato risolto.

Da quando il mittente originale ha creato i puzzle, l’identificatore fa sapere loro quale chiave di sessione ha scoperto il destinatario e le due parti possono utilizzare questa chiave per comunicare in modo più sicuro. Se un utente malintenzionato sta ascoltando l’interazione, avrà accesso a tutti i puzzle, nonché all’identificatore che il destinatario trasmette al mittente originale.

L’identificatore non dice all’attaccante quale chiave di sessione viene utilizzata, quindi l’approccio migliore per decrittografare le informazioni è risolvi tutti i puzzle per scoprire la chiave di sessione corretta. Poiché l’attaccante dovrà risolvere la metà dei puzzle in media, alla fine sarà molto più difficile per loro scoprire la chiave di quanto non lo sia per il destinatario.

Questo approccio offre maggiore sicurezza, ma è tutt’altro che una soluzione perfetta. Lo scambio di chiavi Diffie-Hellman ha preso alcune di queste idee e le ha rese più complesse al fine di creare un metodo sicuro di crittografia a chiave pubblica.

Anche se è diventato noto come lo scambio di chiavi Diffie-Hellman, Martin Hellman ha proposto che l’algoritmo sia chiamato invece lo scambio di chiavi Diffie-Hellman-Merkle, per riflettere il lavoro che Ralph Merkle ha rivolto alla crittografia a chiave pubblica.

Si pensava pubblicamente che Merkle, Hellman e Diffie furono le prime persone a sviluppare la crittografia a chiave pubblica fino al 1997, quando il governo britannico declassificò il lavoro svolto nei primi anni ’70 da James Ellis, Clifford Cox e Malcolm Williamson.

Si scopre che il trio ha inventato il primo schema di crittografia a chiave pubblica tra il 1969 e il 1973, ma il loro lavoro è stato classificato per due decenni. È stato condotto sotto il Government Communication Headquarters (GCHQ), un’agenzia di intelligence britannica.

La loro scoperta fu in realtà l’algoritmo RSA, quindi Diffie, Hellman e Merkle furono ancora i primi a sviluppare lo scambio di chiavi Diffie-Hellman, ma non furono più i primi inventori della crittografia a chiave pubblica.

Dove viene utilizzato lo scambio di chiavi Diffie-Hellman?

Lo scopo principale dello scambio di chiavi Diffie-Hellman è sviluppare in modo sicuro segreti condivisi che possono essere utilizzati per ricavare le chiavi. Questi tasti possono quindi essere utilizzati con algoritmi a chiave simmetrica per trasmettere informazioni in modo protetto. Gli algoritmi simmetrici tendono ad essere utilizzati per crittografare la maggior parte dei dati perché sono più efficienti degli algoritmi a chiave pubblica.

Tecnicamente, lo scambio di chiavi Diffie-Hellman può essere utilizzato per stabilire chiavi pubbliche e private. Tuttavia, in pratica, tende ad essere utilizzato invece RSA. Questo perché l’algoritmo RSA è anche in grado di firmare certificati a chiave pubblica, mentre lo scambio di chiavi Diffie-Hellman non è.

L’algoritmo ElGamal, utilizzato pesantemente in PGP, si basa sullo scambio di chiavi Diffie-Hellman, quindi qualsiasi protocollo che lo utilizza implementa effettivamente una sorta di Diffie-Hellman.

Come uno dei metodi più comuni per la distribuzione sicura delle chiavi, lo scambio di chiavi Diffie-Hellman è spesso implementato in protocolli di sicurezza come TLS, IPsec, SSH, PGP e molti altri. Questo lo rende parte integrante delle nostre comunicazioni sicure.

Come parte di questi protocolli, lo scambio di chiavi Diffie-Hellman viene spesso utilizzato per proteggere la connessione a un sito Web, per accedere in remoto a un altro computer e per inviare e-mail crittografate

Come funziona lo scambio di chiavi Diffie-Hellman?

Lo scambio di chiavi Diffie-Hellman è complesso e può essere difficile capire come funziona. Utilizza numeri molto grandi e molta matematica, qualcosa che molti di noi temono ancora da quelle lunghe e noiose lezioni del liceo.

Per rendere le cose un po ‘più facili da capire, inizieremo spiegando lo scambio di chiavi Diffie-Hellman con un’analogia. Una volta che avrai un’idea generale di come funziona, passeremo a una descrizione più tecnica dei processi sottostanti.

La migliore analogia per lo schema Diffie-Hellman è pensare due persone che mescolano la vernice. Usiamo lo standard di crittografia e diciamo che i loro nomi sono Alice e Bob. Entrambi concordano su un colore casuale per cominciare. Diciamo che si scambiano un messaggio e decidere il giallo come colore comune, proprio come nel diagramma seguente:

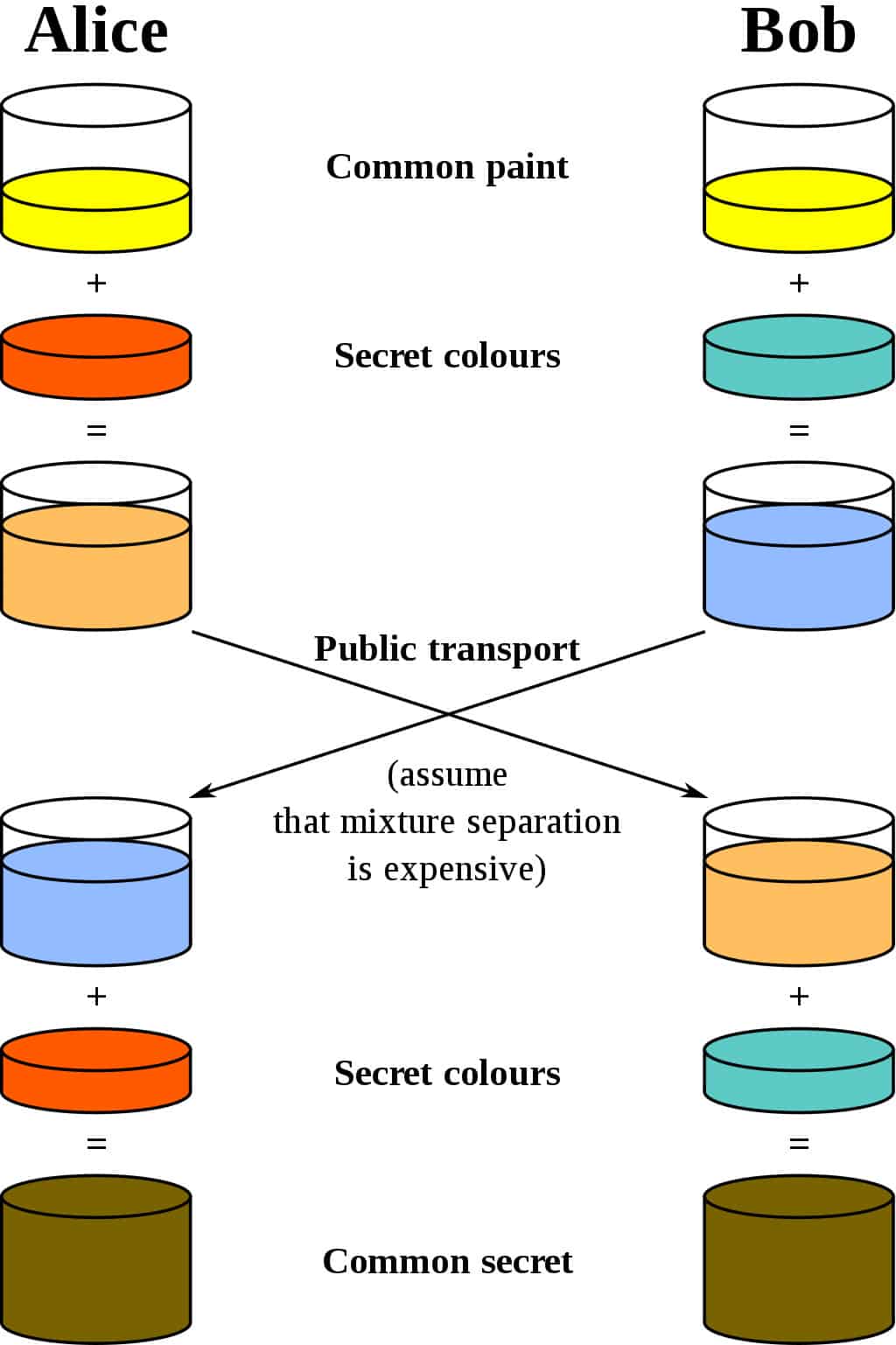
vedere il loro colore segreto. Non dicono all’altra parte la loro scelta. Diciamo che Alice sceglie rosso, mentre Bob sceglie a blu leggermente verdastro.

Il passo successivo è che sia Alice che Bob mescolino il loro colore segreto (rosso per Alice, blu-verdastro per Bob) con il giallo che si erano reciprocamente concordati. Secondo il diagramma, Alice finisce con un mix di arance, mentre il risultato di Bob è a blu più profondo.

Una volta terminata la miscelazione, inviano il risultato all’interlocutore. Alice riceve il blu più profondo, mentre A Bob viene inviata la vernice di colore arancione.

Una volta ricevuto il risultato misto dal loro partner, aggiungono il loro colore segreto. Alice prende il blu più profondo e aggiunge la sua vernice rossa segreta, mentre Bob aggiunge il suo segreto blu-verdastro al mix arancione che ha appena ricevuto.

Il risultato? Entrambi escono con lo stesso colore, che in questo caso è un marrone disgustoso. Potrebbe non essere il tipo di colore con cui vorresti dipingere il tuo salotto, ma è comunque un colore condiviso. Questo colore condiviso è indicato come segreto comune.

La parte fondamentale dello scambio di chiavi Diffie-Hellman è che entrambe le parti finiscono con lo stesso risultato, senza mai dover inviare l’intero segreto comune attraverso il canale di comunicazione. La scelta di un colore comune, i propri colori segreti, lo scambio del mix e quindi l’aggiunta del proprio colore ancora una volta, offre a entrambe le parti un modo per arrivare allo stesso segreto comune senza mai dover passare attraverso tutto.

Se un attaccante sta ascoltando lo scambio, tutto ciò a cui può accedere è il colore giallo comune con cui iniziano Alice e Bob, nonché i colori misti che vengono scambiati. Dal momento che questo è davvero fatto con numeri enormi invece di dipingere, queste informazioni non sono sufficienti per consentire all’attacco di discernere i colori segreti iniziali o il segreto comune (tecnicamente è possibile calcolare il segreto comune da queste informazioni, ma in un’implementazione sicura dello scambio di chiavi Diffie-Hellman, ci vorrebbe una quantità di tempo e risorse computazionali impossibile per farlo).

Questa struttura dello scambio di chiavi Diffie-Hellman è ciò che lo rende così utile. Consente alle due parti di comunicare tramite una connessione potenzialmente pericolosa e di creare un segreto condiviso che possono utilizzare per creare chiavi di crittografia per le loro comunicazioni future. Non importa se alcuni aggressori stanno ascoltando, perché il segreto condiviso completo non viene mai inviato tramite la connessione.

I dettagli tecnici dello scambio di chiavi Diffie-Hellman

Tempo per un po ‘di matematica …

Non preoccuparti, la rallenteremo e proveremo a rendere l’intero processo il più semplice possibile da capire. Segue una premessa simile all’analogia mostrata sopra, ma invece di mescolare e inviare colori, lo schema Diffie-Hellman in realtà effettua calcoli basati su numeri primi eccezionalmente grandi, quindi li trasmette.

Per garantire la sicurezza, si consiglia di prime (p) è lungo almeno 2048 bit, che è l’equivalente binario di un numero decimale di circa questa dimensione:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

Per evitare che la testa di qualcuno esploda, eseguiremo questa spiegazione con numeri molto più piccoli. Fai attenzione a lo scambio di chiavi Diffie-Hellman sarebbe insicuro se usasse numeri piccoli come quelli del nostro esempio. Stiamo usando solo numeri così piccoli per dimostrare il concetto in modo più semplice.

Nella forma più elementare dello scambio di chiavi Diffie-Hellman, Alice e Bob iniziano decidendo reciprocamente su due numeri per cominciare, al contrario della singola vernice comune nell’esempio sopra. Questi sono il modulo (p) e la base (g).

In uso pratico, il modulo (p) è un numero primo molto grande, mentre la base (g) è relativamente piccolo per semplificare i calcoli. La base (g) è derivato da un gruppo ciclico (sol) che viene normalmente generato molto prima che avvengano gli altri passaggi.

Per il nostro esempio, supponiamo che il modulo (p) è 17, mentre la base (g) è 4.

Una volta che si sono reciprocamente decisi su questi numeri, Alice stabilisce un numero segreto (un’) per se stessa, mentre Bob sceglie il suo numero segreto (B). Diciamo che scelgono:

a = 3

b = 6

Alice quindi esegue il seguente calcolo per darle il numero che invierà a Bob:

A = ga mod p

Nel calcolo sopra, mod indica un’operazione modulo. Questi sono essenzialmente calcoli per capire il resto dopo aver diviso il lato sinistro per il diritto. Come esempio:

15 mod 4 = 3

Se capisci come funzionano le operazioni del modulo, puoi eseguirle tu stesso nei seguenti calcoli, altrimenti puoi usare una calcolatrice online.

Quindi mettiamo i nostri numeri nella formula:

A = 43 mod 17

A = 64 mod 17

A = 13

Quando facciamo lo stesso per Bob, otteniamo:

B = 46 mod 17

B = 4096 mod 17

B = 16

Alice quindi invia il suo risultato (UN) a Bob, mentre Bob invia la sua figura (B) ad Alice. Alice quindi calcola il segreto condiviso (S) utilizzando il numero ricevuto da Bob (B) e il suo numero segreto (un’), utilizzando la seguente formula:

S = Ba mod p

S = 163 mod 17

S = 4.096 mod 17

S = 16

Bob quindi esegue quello che è essenzialmente lo stesso calcolo, ma con il numero che Alice gli ha inviato (UN), nonché il suo numero segreto (B):

S = UNB mod p

S = 136 mod 17

S = 4.826.809 mod 17

s = 16

Come puoi vedere, entrambe le parti hanno ottenuto lo stesso risultato S, 16. Questo è il segreto condiviso, che solo Alice e Bob conoscono. Possono quindi utilizzarlo per impostare una chiave per la crittografia simmetrica, consentendo loro di inviare informazioni in modo sicuro tra loro in modo che solo loro possano accedervi.

Si noti che sebbene B e S sono gli stessi nell’esempio sopra, questa è solo una coincidenza basata sui piccoli numeri che sono stati scelti per questa illustrazione. Normalmente, questi valori non sarebbero gli stessi in una vera implementazione dello scambio di chiavi Diffie-Hellman.

Anche se molti dei dati di cui sopra vengono inviati attraverso il canale in chiaro (p, g, A e B) e può essere letto da potenziali aggressori, il segreto condiviso (S) non viene mai trasmesso. Non sarebbe pratico per un utente malintenzionato calcolare il segreto condiviso (S) o uno dei numeri segreti (un’ e B) dalle informazioni inviate in chiaro.

Naturalmente, questo presuppone che lo scambio di chiavi Diffie-Hellman sia correttamente implementato e vengano utilizzati numeri sufficientemente grandi. Fintanto che queste disposizioni sono rispettate, lo scambio di chiavi Diffie-Hellman è considerato un modo sicuro per stabilire un segreto condiviso che può essere utilizzato per proteggere le comunicazioni future.

Stabilire una chiave condivisa tra più parti

Lo scambio di chiavi Diffie-Hellman può anche essere utilizzato per impostare una chiave condivisa con un numero maggiore di partecipanti. Funziona allo stesso modo, tranne che sono necessari ulteriori giri di calcoli per ciascuna parte per aggiungere il proprio numero segreto e finire con lo stesso segreto condiviso.

Proprio come nella versione a due parti dello scambio di chiavi Diffie-Hellman, alcune parti delle informazioni vengono inviate attraverso canali non sicuri, ma non abbastanza per consentire a un utente malintenzionato di calcolare il segreto condiviso.

Perché lo scambio di chiavi Diffie-Hellman è sicuro?

A livello matematico, lo scambio di chiavi Diffie-Hellman si basa su funzioni a senso unico come base per la sua sicurezza. Questi sono calcoli che sono semplici da fare in un modo, ma molto più difficili da calcolare al contrario.

Più specificamente, si basa sul problema Diffie-Hellman, che presuppone che con i giusti parametri non sia possibile calcolare gab dai valori separati di g, gun’ e gB. Al momento non esiste un modo pubblicamente noto per trovarlo facilmente gab dagli altri valori, motivo per cui lo scambio di chiavi Diffie-Hellman è considerato sicuro, nonostante il fatto che gli aggressori possano intercettare i valori p, g, UN, e B.

Autenticazione & lo scambio di chiavi Diffie-Hellman

Nel mondo reale, lo scambio di chiavi Diffie-Hellman è raramente utilizzato da solo. Il motivo principale dietro questo è quello non fornisce alcuna autenticazione, il che rende gli utenti vulnerabili agli attacchi man-in-the-middle.

Questi attacchi possono aver luogo quando lo scambio di chiavi Diffie-Hellman è implementato da solo, perché non ha alcun mezzo per verificare se l’altra parte in una connessione è davvero chi dicono di essere. Senza alcuna forma di autenticazione, gli utenti potrebbero effettivamente connettersi con gli aggressori quando pensano di comunicare con una parte fidata.

Per questo motivo, lo scambio di chiavi Diffie-Hellman viene generalmente implementato insieme ad alcuni mezzi di autenticazione. Ciò comporta spesso l’uso di certificati digitali e un algoritmo a chiave pubblica, come RSA, per verificare l’identità di ciascuna parte.

Variazioni dello scambio di chiavi Diffie-Hellman

Lo scambio di chiavi Diffie-Hellman può essere implementato in diversi modi e ha anche fornito la base per numerosi altri algoritmi. Alcune di queste implementazioni forniscono l’autorizzazione, mentre altre hanno varie funzionalità crittografiche come il perfetto segreto in avanti.

Diffie-Hellman a curva ellittica

Diffie-Hellman a curva ellittica sfrutta la struttura algebrica delle curve ellittiche per consentire alle sue implementazioni di raggiungere un livello di sicurezza simile con una dimensione della chiave più piccola. Una chiave a curva ellittica a 224 bit offre lo stesso livello di sicurezza di una chiave RSA a 2048 bit. Ciò può rendere gli scambi più efficienti e ridurre i requisiti di archiviazione.

A parte la minore lunghezza della chiave e il fatto che si basa sulle proprietà delle curve ellittiche, Diffie-Hellman a curva ellittica opera in modo simile allo scambio di chiavi Diffie-Hellman standard.

TLS   

TLS, che è un protocollo utilizzato per proteggere gran parte di Internet, può utilizzare lo scambio Diffie-Hellman in tre modi diversi: anonimo, statico ed effimero. In pratica, dovrebbe essere implementato solo il effimero Diffie-Hellman, perché le altre opzioni hanno problemi di sicurezza.

• Anonimo Diffie-Hellman – Questa versione dello scambio di chiavi Diffie-Hellman non utilizza alcuna autenticazione, rendendola vulnerabile agli attacchi man-in-the-middle. Non dovrebbe essere usato o implementato.
• Diffie-Hellman statico – Static Diffie-Hellman utilizza i certificati per autenticare il server. Non autentica il client per impostazione predefinita, né fornisce segretezza diretta.
• Diffie-Hellman effimero – Questa è considerata l’implementazione più sicura perché fornisce un perfetto segreto in avanti. È generalmente combinato con un algoritmo come DSA o RSA per autenticare una o entrambe le parti nella connessione. Effimero Diffie-Hellman utilizza coppie di chiavi diverse ogni volta che viene eseguito il protocollo. Ciò fornisce alla connessione un perfetto segreto in avanti, perché anche se una chiave viene compromessa in futuro, non può essere utilizzata per decrittografare tutti i messaggi passati.

ElGamal

ElGamal è un algoritmo a chiave pubblica basato sullo scambio di chiavi Diffie-Hellman. Come Diffie-Hellman, non contiene disposizioni per l’autenticazione da solo e viene generalmente combinato con altri meccanismi per questo scopo.

ElGamal veniva utilizzato principalmente in PGP, GNU Privacy Guard e altri sistemi perché il suo principale rivale, RSA, era brevettato. Il brevetto di RSA è scaduto nel 2000, il che ha permesso di implementarlo liberamente dopo tale data. Da allora, ElGamal non è stato implementato così frequentemente.

STS

Il protocollo Station-to-Station (STS) si basa anche sullo scambio di chiavi Diffie-Hellman. È un altro schema di accordo chiave, tuttavia fornisce protezione contro gli attacchi man-in-the-middle e un perfetto segreto in avanti.

Richiede che entrambe le parti nella connessione abbiano già una coppia di chiavi, che viene utilizzata per autenticare ciascuna parte. Se le parti non si conoscono già, è possibile utilizzare i certificati per convalidare le identità di entrambe le parti.

Lo scambio di chiavi Diffie-Hellman & RSA

Come abbiamo discusso in precedenza, lo scambio di chiavi Diffie-Hellman viene spesso implementato insieme a RSA o altri algoritmi per fornire l’autenticazione per la connessione. Se hai familiarità con RSA, ti starai chiedendo perché qualcuno si preoccuperebbe di usare anche lo scambio di chiavi Diffie-Hellman, poiché RSA consente alle parti che non si sono mai incontrate in precedenza di comunicare in modo sicuro.

RSA consente ai suoi utenti di crittografare i messaggi con la chiave pubblica del loro corrispondente, in modo che possano essere decodificati solo dalla chiave privata corrispondente. Tuttavia, in pratica, RSA non viene utilizzato per crittografare la totalità delle comunicazioni: sarebbe troppo inefficiente.

Invece, RSA viene spesso utilizzato solo come mezzo per autenticare entrambe le parti. Lo fa con i certificati digitali di ciascuna parte, che saranno stati verificati da un’autorità di certificazione per dimostrare che il proprietario di un certificato è veramente chi afferma di essere e che la chiave pubblica sul certificato appartiene effettivamente a lui.

Per l’autenticazione reciproca, ciascuna parte firmerà un messaggio utilizzando la propria chiave privata e quindi lo invierà al proprio partner di comunicazione. Ogni destinatario può quindi verificare l’identità dell’altra parte controllando i messaggi firmati con la chiave pubblica sul certificato digitale del proprio partner di comunicazione (vedi l’articolo sopra menzionato su RSA per maggiori dettagli su come funziona, in particolare il Firma dei messaggi sezione).

Ora che entrambe le parti sono state autenticate, è tecnicamente possibile continuare a utilizzare RSA per inviare messaggi crittografati in modo sicuro tra di loro, tuttavia sarebbe troppo inefficiente.

Per ovviare a questa inefficienza, molti protocolli di sicurezza utilizzano un algoritmo come lo scambio di chiavi Diffie-Hellman per trovare un segreto comune che può essere usato per stabilire una chiave simmetrica condivisa. Questa chiave simmetrica viene quindi utilizzata in un algoritmo a chiave simmetrica, come AES, per crittografare i dati che le due parti intendono inviare in modo sicuro tra loro.

Può sembrare un processo complesso e contorto, ma finisce per essere molto più rapido e meno impegnativo in termini di risorse rispetto all’utilizzo di un algoritmo a chiave pubblica per l’intero scambio. Questo è perché la crittografia a chiave simmetrica è ordini di grandezza più efficienti della crittografia a chiave pubblica.

Oltre alle inefficienze che abbiamo appena menzionato, ci sono alcuni altri aspetti negativi che verrebbero dal solo utilizzo di RSA. RSA ha bisogno di imbottitura per renderlo sicuro, quindi un algoritmo aggiuntivo dovrebbe essere implementato in modo appropriato accanto ad esso per renderlo sicuro.

RSA non fornisce un perfetto segreto in avanti, sia, che è un altro svantaggio rispetto allo scambio di chiavi effimero Diffie-Hellman. Collettivamente, questi motivi sono il motivo per cui, in molte situazioni, è meglio applicare RSA solo in combinazione con lo scambio di chiavi Diffie-Hellman.

In alternativa, lo scambio di chiavi Diffie-Hellman può essere combinato con un algoritmo come il Digital Signature Standard (DSS) per fornire autenticazione, scambio di chiavi, riservatezza e controllo dell’integrità dei dati. In tale situazione, RSA non è necessario per proteggere la connessione.

Problemi di sicurezza dello scambio di chiavi Diffie-Hellman

La sicurezza dello scambio di chiavi Diffie-Hellman dipende da come viene implementata, nonché dai numeri scelti per questo. Come abbiamo detto sopra, non ha alcun mezzo per autenticare l’altra parte da solo, ma in pratica vengono utilizzati altri meccanismi per garantire che l’altra parte in una connessione non sia un impostore.

Parametri per la selezione del numero

Se un’implementazione nel mondo reale dello scambio di chiavi Diffie-Hellman usasse numeri piccoli come quelli del nostro esempio, renderebbe il processo di scambio banale per un aggressore che si spezzasse. Ma non è solo la dimensione dei numeri che conta: i numeri devono anche essere sufficientemente casuali. Se un generatore di numeri casuali produce un output prevedibile, può compromettere completamente la sicurezza dello scambio di chiavi Diffie-Hellman.

Il numero p dovrebbe essere lungo 2048 bit per garantire la sicurezza. La base, g, può essere un numero relativamente piccolo come 2, ma deve provenire da un ordine di sol questo ha un grande fattore primo

L’attacco di Logjam

Lo scambio di chiavi Diffie-Hellman è stato progettato sulla base del problema del logaritmo discreto che è difficile da risolvere. Il meccanismo più efficace noto pubblicamente per trovare la soluzione è l’algoritmo di setaccio del campo numerico.

Le capacità di questo algoritmo sono state prese in considerazione quando è stato progettato lo scambio di chiavi Diffie-Hellman. Nel 1992, era noto che per un determinato gruppo, sol, tre dei quattro passaggi coinvolti nell’algoritmo potrebbero essere potenzialmente calcolati in anticipo. Se questo progresso fosse salvato, il passaggio finale potrebbe essere calcolato in un tempo relativamente breve.

Ciò non era troppo preoccupante fino a quando non si è realizzato che una parte significativa del traffico Internet utilizza gli stessi gruppi di 1024 bit o più piccoli. Nel 2015, un team accademico ha eseguito i calcoli per il più comune prime a 512 bit utilizzato dallo scambio di chiavi Diffie-Hellman in TLS.

Sono stati anche in grado di eseguire il downgrade dell’80% dei server TLS che supportavano DHE-EXPORT, in modo da accettare uno scambio di chiavi Diffie-Hellman a livello di esportazione a 512 bit per la connessione. Ciò significa che ciascuno di questi server è vulnerabile a un attacco di un avversario dotato di risorse adeguate.

I ricercatori hanno continuato a estrapolare i loro risultati, stimando che uno stato-nazione potrebbe rompere un numero primo a 1024 bit. Rompendo il singolo primo a 1024 bit più comunemente usato, il team accademico ha stimato che un avversario potrebbe monitorare il 18% del milione di siti Web HTTPS più popolari.

Hanno continuato dicendo che un secondo primo avrebbe consentito all’avversario di decrittografare le connessioni del 66% dei server VPN e del 26% dei server SSH. Più avanti nel rapporto, gli accademici hanno suggerito che la NSA potrebbe già avere queste capacità.

“Una lettura attenta delle fughe pubblicate dalla NSA mostra che gli attacchi dell’agenzia alle VPN sono coerenti con il raggiungimento di tale interruzione.”

Nonostante questa vulnerabilità, lo scambio di chiavi Diffie-Hellman può ancora essere sicuro se implementato correttamente. Finché viene utilizzata una chiave a 2048 bit, l’attacco Logjam non funzionerà. Anche i browser aggiornati sono sicuri da questo attacco.

Lo scambio di chiavi Diffie-Hellman è sicuro?

Sebbene lo scambio di chiavi Diffie-Hellman possa sembrare complesso, è una parte fondamentale dello scambio sicuro di dati online. Finché è implementato insieme a un metodo di autenticazione appropriato e i numeri sono stati selezionati correttamente, non è considerato vulnerabile agli attacchi.

Lo scambio di chiavi Diffie-Hellman era un metodo innovativo per aiutare due parti sconosciute a comunicare in sicurezza quando fu sviluppato negli anni ’70. Mentre ora implementiamo versioni più recenti con chiavi più grandi per proteggerci dalle moderne tecnologie il protocollo stesso sembra che continuerà ad essere sicuro fino all’arrivo dell’informatica quantistica e gli attacchi avanzati che ne conseguiranno.

Tecnologia aziendale per la sicurezza informatica da TheDigitalArtist su licenza CC0