Che cos’è la crittografia 3DES e come funziona DES?

3DES è un codice di crittografia derivato dal Data Encryption Standard (DES) originale. È diventato importante alla fine degli anni Novanta, ma da allora è caduto in disgrazia a causa dell’ascesa di algoritmi più sicuri.

Anche se sarà deprecato nel 2023, è ancora implementato in alcune situazioni. Poiché si basa su uno dei primi algoritmi ampiamente pubblicati e studiati, DES, è ancora importante conoscere cos’è 3DES e come funziona.

Questa guida ti guiderà in dettaglio in ogni fase del processo DES, quindi illustrerà come il DES viene modificato in 3DES per renderlo più sicuro. Tocca anche i vari problemi di sicurezza e se è necessario utilizzare l’algoritmo.

Che cos’è 3DES?

Sebbene sia ufficialmente noto come Triple Data Encryption Algorithm (3DEA), viene comunemente chiamato 3DES. Questo perché l’algoritmo 3DES utilizza la crittografia Data Encryption Standard (DES) tre volte per crittografare i suoi dati.

DES è un algoritmo a chiave simmetrica basato su una rete Feistel. Come codice di chiave simmetrica, utilizza la stessa chiave per i processi di crittografia e decrittografia. La rete Feistel rende entrambi questi processi quasi identici, il che si traduce in un algoritmo che è più efficiente da implementare.

DES ha sia un blocco a 64 bit che la dimensione della chiave, ma in pratica la chiave garantisce solo 56 bit di sicurezza. 3DES è stato sviluppato come alternativa più sicura a causa della ridotta lunghezza della chiave DES. In 3DES, l’algoritmo DES viene eseguito tre volte con tre chiavi, tuttavia è considerato sicuro solo se vengono utilizzate tre chiavi separate.

Gli usi di 3DES

Una volta che i punti deboli del DES normale sono diventati più evidenti, 3DES è stato adottato in una vasta gamma di applicazioni. Era uno degli schemi di crittografia più comunemente usati prima dell’ascesa di AES.

Alcuni esempi delle sue implementazioni includono i sistemi di pagamento Microsoft Office, Firefox ed EMV. Molte di queste piattaforme non usano più 3DES perché ci sono alternative migliori.

Il National Institute of Standards and Technology (NIST) ha pubblicato un progetto di proposta in cui afferma che tutte le forme di 3DES saranno deprecate fino al 2023 e vietate dal 2024 in poi. Sebbene sia solo una bozza, la proposta indica la fine di un’era ed è ormai passato il tempo per passare ad altri algoritmi più sicuri.

La storia della crittografia 3DES

Poiché 3DES è derivato da DES, è meglio introdurre prima lo standard precedente. Negli anni settanta, il National Bureau of Standards (NBS – da allora è stato ribattezzato NIST) era alla ricerca di un algoritmo che potesse utilizzare come standard per crittografare informazioni governative sensibili ma non classificate.

L’NBS ha accettato le proposte per uno standard che si adattasse ai suoi requisiti, ma nessuno dei candidati del round originale era appropriato. Ha invitato più invii e questa volta IBM ha inviato un algoritmo sviluppato dal suo team. La presentazione derivava dal codice Lucifer progettato da Horst Feistel.

Nel 1975, l’algoritmo IBM fu pubblicato dalla NBS come proposto Standard di crittografia dei dati. Il pubblico è stato invitato a commentare il design, che ha suscitato alcune critiche.

Criptografi di spicco come Whitfield Diffie e Martin Hellman, progettisti dello scambio di chiavi Diffie-Hellman, affermarono che la lunghezza della chiave era troppo corta e che le S-box erano state cambiate rispetto al loro progetto iniziale.

All’epoca, molti nella comunità crittografica pensavano che l’NSA avesse sabotato il progetto e indebolito l’algoritmo, in modo che fosse l’unica agenzia in grado di rompere DES.

Quando questo è stato indagato dal Comitato per l’Intelligence del Senato degli Stati Uniti, è emerso che “la NSA ha convinto IBM che una dimensione chiave ridotta era sufficiente; assistenza indiretta nello sviluppo delle strutture S-box; e ha certificato che l’algoritmo DES finale era, per quanto a sua conoscenza, libero da qualsiasi debolezza statistica o matematica. “

Lo stesso rapporto prosegue affermando che “NSA non ha alterato in alcun modo il design”. Questo è stato supportato da un ex staff IBM che ha affermato che l’algoritmo DES è stato progettato interamente dal team IBM.

La documentazione declassificata dell’NSA afferma che l’agenzia “ha lavorato a stretto contatto con IBM per rafforzare l’algoritmo contro tutti tranne gli attacchi di forza bruta e per rafforzare le tabelle di sostituzione …”

I sospetti di manomissione della NSA furono allentati negli anni novanta dopo che la crittoanalisi differenziale fu scoperta pubblicamente. Quando le S-box molto diffamate furono testate con la nuova tecnica, si scoprì che erano più resistenti agli attacchi che se fossero state scelte a caso.

Ciò indica che il team IBM aveva già saputo della crittoanalisi differenziale negli anni Settanta, con Steven Levy che sosteneva che l’NSA aveva chiesto loro di mantenere segreta la tecnica per proteggere la sicurezza nazionale.

Il famoso crittografo Bruce Schneier una volta ha scherzato, “Ci sono voluti due decenni alla comunità accademica per capire che i” ritocchi “della NSA hanno effettivamente migliorato la sicurezza del DES”.

Nonostante le domande iniziali sulla sicurezza dell’algoritmo e il coinvolgimento dell’NSA, l’algoritmo IBM è stato approvato come Standard di crittografia dei dati nel 1976. È stato pubblicato nel 1977 e ribadito come standard nel 1983, 1988 e 1993.

Quando la crittoanalisi lineare è stata pubblicata per la prima volta nel 1994, ha iniziato a sollevare domande sulla sicurezza dell’algoritmo. Nel 1997, NIST ha annunciato che stava cercando un algoritmo per sostituire DES. La necessità di un nuovo algoritmo è stata intensificata man mano che la tecnologia si sviluppava ulteriormente e i potenziali attacchi diventavano più forti.

Vari tentativi di cracking hanno mostrato che era meno difficile rompere l’algoritmo di quanto si pensasse in precedenza. Nel 1998, distribut.net è stato in grado di decifrare DES in 39 giorni.

All’inizio del 1999, Deep Crack della Electronic Frontier Foundation aveva ridotto il tempo a poco più di 22 ore. Ciò ha segnato la fine del DES, poiché un attacco di questa natura era ora alla portata di un avversario dotato di risorse adeguate..

Il problema principale era il piccolo spazio chiave e un nuovo algoritmo era estremamente necessario. Questo era un problema, perché ci sarebbero voluti diversi anni prima che il NIST si accontentasse dell’algoritmo che è diventato lo standard sostitutivo, lo standard di crittografia avanzata (AES).

Mentre veniva deciso il codice per AES, 3DES è stato proposto come misura di stopgap. Implica l’esecuzione dell’algoritmo DES tre volte, con tre chiavi separate. Nel 1999, DES è stato ribadito, ma con 3DES come algoritmo ideale. Il DES normale era consentito solo nelle applicazioni legacy.

3DES ha continuato a diventare un algoritmo di crittografia diffuso, sebbene il suo uso intenso di risorse e le limitazioni di sicurezza lo abbiano portato a essere sostituito da AES nella maggior parte dei casi d’uso.

Comprensione dell’algoritmo DES

Prima di poter parlare dei dettagli di 3DES, è importante capire l’algoritmo DES da cui deriva. Quindi iniziamo subito.

Usiamo la crittografia per trasformare i nostri dati in chiaro in testo cifrato, ovvero informazioni a cui non possono accedere gli aggressori (purché utilizziamo algoritmi appropriati).

Gli algoritmi di crittografia sono formule matematiche essenzialmente complesse. Quando si tratta di crittografare qualcosa come “Andiamo in spiaggia”, molte persone si confondono. Dopo tutto, come puoi applicare la matematica a cose come lettere e caratteri?

Codifica del testo

La realtà è che i computer non si occupano di lettere e caratteri. Invece, funzionano su un sistema di 1 e 0 noto come binario. Ogni 1 o 0 è noto come un bit e una raccolta di otto di essi è nota come byte.

Puoi cercarlo manualmente o utilizzare un convertitore online per vedere che in binario, “Andiamo in spiaggia” diventa:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

blocchi

Quando i dati sono crittografati, vengono divisi in blocchi separati per l’elaborazione. DES ha una dimensione di blocco a 64 bit, il che significa essenzialmente che ogni blocco si adatta a un mix di 64 e zero. Il nostro primo blocco (le prime 64 cifre del binario mostrato sopra) sarebbe:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Il nostro secondo sarebbe:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

E il nostro blocco finale sarebbe:

01100010 01100101 01100001 01100011 01101000

Imbottitura

Forse avrai notato che il nostro terzo blocco è lungo solo 40 bit. Prima che possa essere crittografato, deve essere costruito fino a una dimensione di blocco a 64 bit. Questo è fatto con imbottitura, che comporta l’aggiunta di ulteriori informazioni a un blocco per completarlo. Questo può essere fatto con una serie di schemi diversi e può anche servire a rendere le informazioni crittografate più difficili da decifrare, ma non ci occuperemo di ciò in questo articolo.

La pianificazione dei tasti DES

Gli algoritmi di crittografia utilizzano le chiavi per aggiungere dati che alterano il risultato finale del processo. Se DES ha comportato solo passaggi come permutazione e caselle S (la permutazione è spiegata di seguito, mentre le caselle S sono coperte in Sostituzione sezione), tutto ciò che un utente malintenzionato dovrebbe fare è scoprire i dettagli dell’algoritmo, quindi eseguire ciascuno dei passaggi al contrario per rivelare il messaggio iniziale.

Poiché la maggior parte dei nostri algoritmi è ampiamente nota, ciò non aggiungerebbe molta sicurezza. Invece, vengono aggiunte chiavi segrete per modificare l’output in un modo che non può essere previsto solo conoscendo l’algoritmo (purché venga utilizzato un algoritmo sufficientemente complesso).

DES inizia con una singola chiave, che viene utilizzata per creare sottochiavi che vengono applicate in ogni round. Questa è una chiave a 64 bit, che ha le stesse dimensioni dei nostri blocchi. Diciamo che la nostra chiave è:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Ora, questa chiave in binario, che è il modo in cui i dati vengono espressi quando i computer li elaborano. Quando gli umani hanno a che fare con le chiavi, appariranno normalmente come un mix di personaggi, qualcosa del genere:

kj329nf982bc9wn1

In DES, il primo passo per derivare le nostre chiavi rotonde è permutare la chiave (spostarla) secondo la seguente tabella:

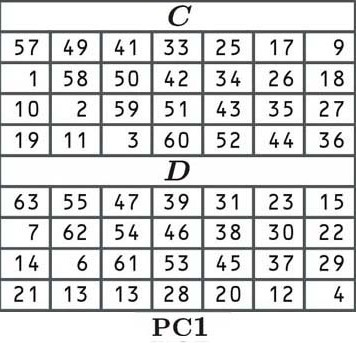
Nella permutazione, ogni bit della nostra chiave originale viene spostato in una nuova posizione come indicato dalla tabella. Dal momento che la cella nell’angolo in alto a sinistra (di C) dice 57, il primo numero della nostra chiave consentita sarà il numero nella 57a posizione del nostro vecchio blocco:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

La seconda cella dice 49, il che significa che la seconda cifra della nostra nuova chiave sarà il numero che si trova nella 49a posizione del nostro vecchio blocco:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

La terza cella dice 41, quindi cerchiamo la cifra nella 41a posizione:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Finora, la nostra chiave è composta da “110”.

Il resto della chiave è organizzato allo stesso modo, in base ai valori della tabella. Ci spostiamo da sinistra a destra e una volta arrivati ​​alla fine di una fila, passiamo alla successiva, proprio come di consueto. Una volta tabella C è finito, saltiamo a tabella D per completare la seconda metà della chiave.

Non esiste un modo semplice per trasporre l’intero blocco in base alla tabella di permutazione iniziale. Potresti fare tutto manualmente o scrivere una sceneggiatura (o anche essere fortunato e trovarne uno nelle profondità di Internet), ma trufferemo e inventeremo:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

Potresti essere preoccupato che stiamo inventando alcuni dei numeri in questa guida, ma la realtà è che non importa davvero. Nessuno cripta più i dati manualmente, tutto avviene tramite programmi. L’aspetto più critico di questo tutorial è che hai un’idea chiara dei concetti con cui abbiamo a che fare. I numeri stessi servono solo per aiutarti a visualizzare cosa sta succedendo.

Alcuni lettori potrebbero aver notato che la tabella (e ora la nostra chiave) ha solo 56 bit anziché 64. Questo perché ogni ottavo bit viene ignorato. Questo è un artefatto dei vecchi tempi della tecnologia, quando era importante disporre di bit di controllo di parità, che verificavano che la chiave fosse stata ricevuta correttamente. Questi bit di controllo di parità indicano che, in pratica, DES ha solo la sicurezza di una chiave a 56 bit.

Le tabelle C e D ci danno una chiave che ha due metà a 28 bit. A volte, le metà sono indicate come C e D, ma in questo articolo faremo riferimento a loro come L e R, per sinistra e destra. La nostra parte di sinistra è:

1100010 1010010 1010101 0101010

Mentre il nostro diritto è:

1010000 1111001 0001011 1000111

Il passo successivo è spostare la chiave di uno o due spazi a sinistra, a seconda del round. Il numero esatto di spazi viene deciso in base alla seguente tabella predeterminata:

Numero rotondo Numero di turni a sinistra

1	1
2	1
3	2
4	2
5	2
6	2
7	2
8	2
9	1
10	2
11	2
12	2
13	2
14	2
15	2
16	1

Quindi prendiamo le nostre metà sinistra e destra:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

E sposta entrambi di una posizione a sinistra, poiché il primo round ha uno spostamento di 1 secondo la tabella (il numero sull’estremità sinistra viene spostato sull’estremità destra).

Sottochiave al primo turno:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

Nel secondo turno, dice anche la tabella 1, quindi questo risultato verrà nuovamente modificato spostando ogni posizione numero uno a sinistra.

Secondo round sottochiave:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

Nel terzo turno, i numeri verranno spostati di due posizioni a sinistra, perché ora la tabella dice 2.

Sottochiave del terzo turno:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

Nei round successivi, i numeri vengono spostati a sinistra in base alle distanze specificate nella tabella, con ogni turno applicato al risultato del round precedente. Alla fine, questo ci dà sedici diverse sottochiavi, una per ogni round del processo DES.

Il passaggio successivo è un’altra permutazione secondo la tabella PC2 mostrata di seguito:

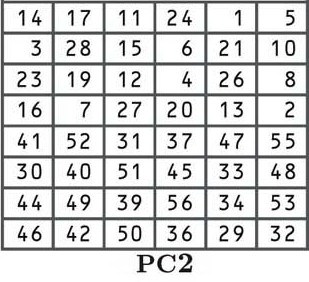
Ormai dovresti avere familiarità con le permutazioni, quindi non entreremo nel processo in modo approfondito. Se vuoi vedere come funziona in modo più dettagliato, fai riferimento alla spiegazione vicino all’inizio di questa sezione. Sebbene le posizioni di trasferimento siano diverse, il processo è lo stesso.

Ognuno dei 16 tasti derivati ​​nel processo di cambio ora viene mischiato secondo la tabella, con il numero dalla 14a posizione spostato al primo posto, dal 17 ° al secondo, dall’11 ° al terzo, ecc…

Se osservi attentamente la tabella, noterai che ci sono solo 48 bit, anziché i 56 bit che avevamo in precedenza. Questo processo è noto come permutazione della compressione.

Puoi anche vedere che la metà superiore della tabella presenta numeri compresi tra 1 e 28, mentre la metà inferiore contiene numeri da 29 a 56. Ciò mantiene separate le metà sinistra e destra delle nostre sottochiavi ed è indicata di seguito dallo spazio più grande nel mezzo delle chiavi.

Ancora una volta, trufferemo e trucceremo i numeri. Supponiamo che l’intero processo ci abbia fornito le seguenti sottochiavi:

Primo round:         010101 010101 101010 110100 101001 100101 101010 101010

Secondo round:         011010 110101 101110 110010 010100 110010 111101 101101

Terzo round:     010100 100110 110110 101010 100110 011000 101011 011001

Quarto round:         011001 110101 011001 110101 000011 001011 010101 010101

Quinto round:         110101 001101 010101 010101 010011 001011 010111 100101

Round sei:           010111 110101 011001 111001 101001 100101 101010 101010

Round 7:     110101 111010 101110 101010 100110 010110 111011 001110

Ottavo round:       011001 110101 010101 001001 010011 001011 010100 101010

Round nono:         111011 011010 011110 100010 100010 010110 110011 110010

Round 10:             011010 010101 101110 101001 010010 010110 111000 101010

Round 11:             110101 001101 101110 101010 100101 100101 101010 001010

Round 12:             101001 100100 101001 101010 100110 011000 101011 011001

Round 13:             010010 010010 010101 010101 010110 110001 100101 101010

Round 14:             101001 100110 010101 011101 010001 001010 110010 111110

Round 15:             011001 011010 011001 110101 001001 011001 100101 101101

Round 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Questo processo di spostamento comporta l’utilizzo di ogni bit della chiave iniziale in circa 14 delle 16 sottochiavi, sebbene alcuni bit vengano utilizzati leggermente più di altri.

Permutazione iniziale

Una volta che i dati sono stati divisi in blocchi e riempiti se necessario, è il momento di iniziare il processo di crittografia DES. Torneremo alle sottochiavi che abbiamo appena creato in una fase successiva. Il primo passaggio è noto come permutazione iniziale, in cui i dati vengono riorganizzati secondo la seguente tabella:

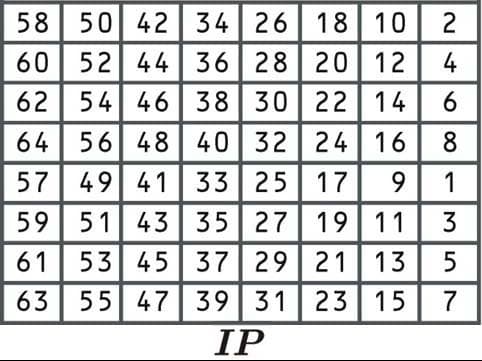
Questo processo di permutazione iniziale non rende l’algoritmo più sicuro. Questo perché non comporta l’inserimento di alcun tasto e può essere facilmente invertito. L’algoritmo è stato originariamente progettato in questo modo perché rendeva più semplice l’implementazione in determinati contesti.

Dato che abbiamo coperto le permutazioni un paio di volte, salteremo qualsiasi spiegazione importante qui. Torna a La pianificazione dei tasti DES se hai bisogno di maggiori informazioni su come funzionano.

Prendiamo il primo blocco dal messaggio “Andiamo in spiaggia”, che abbiamo derivato nel Bloccare sezione sotto Comprensione dell’algoritmo DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Dal momento che la prima cella dice 58, selezioneremmo il numero dalla 58a posizione:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Quindi prenderemo il numero dalla 50a posizione:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

E il numero dalla 42a posizione:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Questo ci dà “110” finora. Tratteremo il resto del numero:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Al termine della permutazione iniziale, i dati vengono spostati al passaggio successivo.

Dividere i blocchi

Una volta che i dati hanno subito la permutazione iniziale, vengono divisi in due metà. Prendiamo il nostro blocco che ha appena subito la sua permutazione iniziale:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

E lo separeremo in due blocchi, un blocco a sinistra (composto dalle prime 32 cifre), noto come L0:

L0    11010111 01001010 10101000 10011101

E un blocco a destra (composto dalle seconde 32 cifre), noto come R0:

R0    01001011 10110101 10000111 10101001

La funzione F.

Ora che il blocco è stato diviso, è tempo che la funzione F abbia luogo. Nel primo round, verrà applicato solo alla metà destra del blocco, mentre la metà sinistra verrà tenuta da parte fino a dopo. Il lato destro subisce i seguenti quattro passaggi come parte della funzione F:

• Permutazione di espansione (E nel diagramma)
• Key mixing (⊕ nel diagramma)
• Sostituzione (ogni S1, S2 ecc. Nel diagramma)
• Permutazione (P nel diagramma)

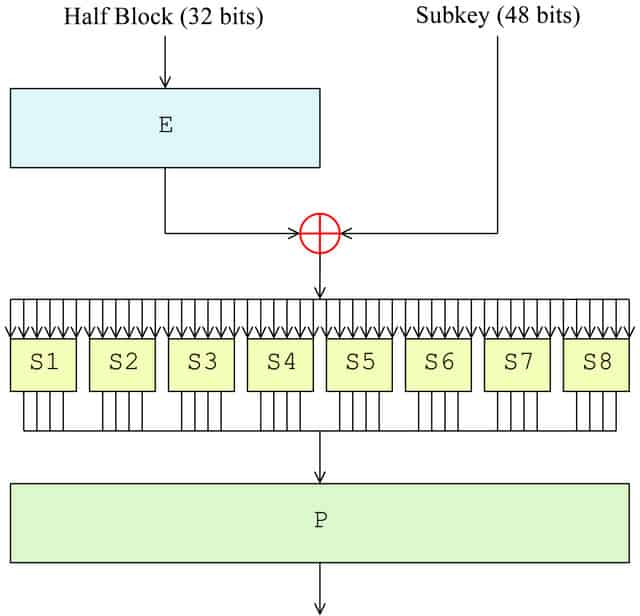
Permutazione di espansione

La permutazione di espansione realizza tre cose. Il più importante è che consente a singoli bit di dati di input di influire sull’uscita di altri due bit, causando un effetto valanga. Crea anche la metà giusta a 48 bit, in modo che abbia le stesse dimensioni della sottochiave per il passaggio successivo. L’altro effetto della permutazione di espansione è che rende l’uscita più lunga dell’ingresso. Ciò consente di comprimerlo nell’operazione di sostituzione.

I bit sono riorganizzati secondo la tabella seguente. Alcuni dei singoli bit sono nella tabella due volte, ed è così che il blocco si è espanso da 32 a 48 bit:

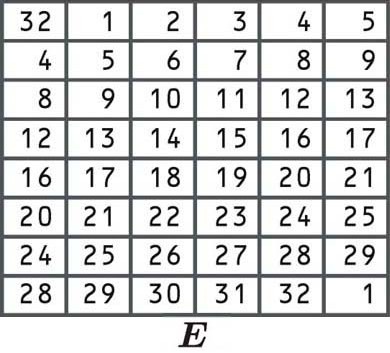
Poiché la prima cella dice 32, prendiamo il nostro blocco destro e selezioniamo il numero dalla 32a posizione, proprio come abbiamo fatto negli altri esempi di permutazione sopra elencati:

R0    01001011 10110101 10000111 10101001

Quindi prendiamo i numeri dalla prima posizione, dalla seconda posizione e così via, fino a quando arriviamo all’angolo in basso a destra del blocco. Dal momento che c’è un 1 in questa cella, l’ultima cifra sarà anche il numero che appare nella prima posizione del nostro blocco.

Supponiamo che la permutazione di espansione ci dia un nuovo blocco a 48 bit di:

101110 100110 100100 000000 001100 001110 101101 011110

Miscelazione chiave

Una volta che il blocco è stato espanso a 48 bit, è tempo di applicare la sottochiave del primo round, che abbiamo derivato nella Pianificazione chiave DES sezione sopra. Il blocco viene modificato dalla sottochiave usando il codice XOR.

La cifra XOR è una cifra aggiuntiva che segue un processo semplice, soprattutto se confrontata con gli altri elementi di cui abbiamo già discusso.

In un codice XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Quindi supponiamo che tu debba XOR i seguenti due numeri in binario:

1101

0101

Ogni cifra verrebbe aggiunta a quella sottostante. Secondo le tre regole sopra indicate, questo dà un risultato di:

1000

Per completare la fase di mixaggio della chiave, prendiamo il lato destro del nostro blocco che abbiamo appena espanso a 48 bit e la prima chiave rotonda. Quindi eseguiamo l’aggiunta XOR:

Bloccare:                      101110 100110 100100 000000 001100 001110 101101 011110

Tasto rotondo:     010101 010101 101010 110100 101001 100101 101010 101010

Risultato XOR:             111011 110011 001110 110100 100101 101011 000111 110100

Il risultato dell’operazione XOR viene quindi passato al round successivo.

Sostituzione

La sostituzione aggiunge confusione ai dati. Normalmente viene eseguito con le tabelle di ricerca, note anche come caselle di sostituzione o S-box. DES utilizza otto tabelle o caselle S separate, una diversa per ogni 6 bit di dati. La tabella seguente mostra le otto S-box di DES:

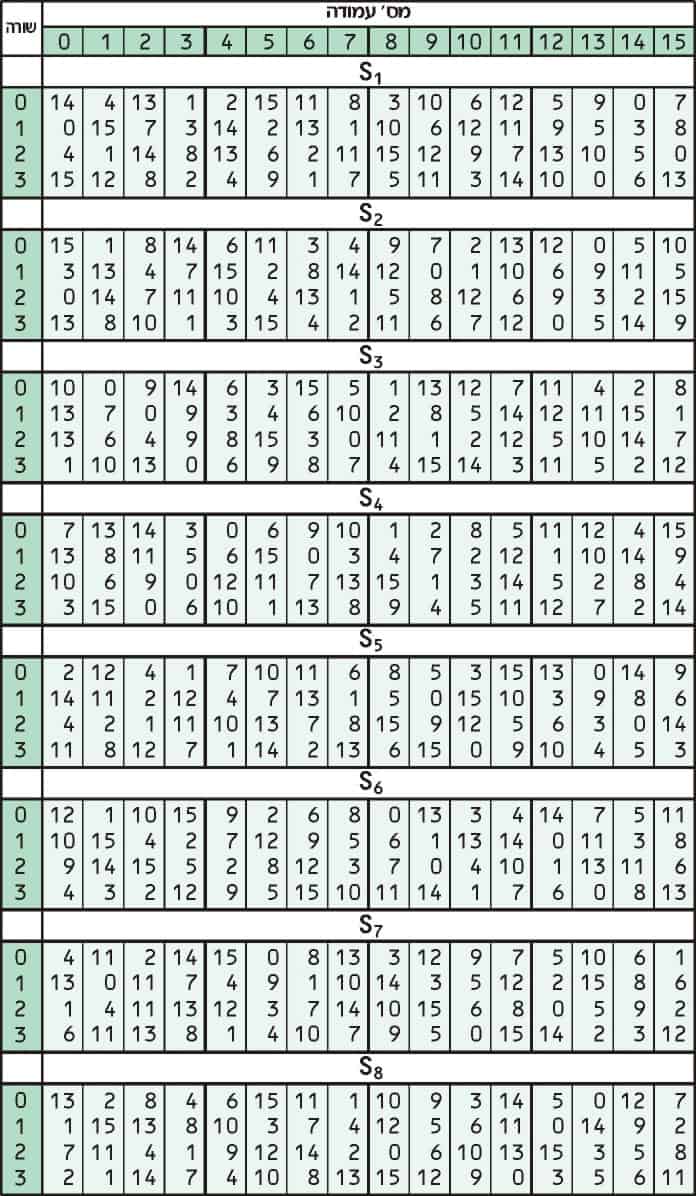
Le otto caselle S separate vengono utilizzate per tradurre ciascun ingresso a 6 bit in un output a 4 bit. Il primo passo del processo è prendere le cifre all’inizio e alla fine di un segmento a 6 bit, quindi convertire quel valore binario in decimale.

Prendiamo i dati che abbiamo appena finito XORing nel passaggio precedente:

111011 110011 001110 110100 100101 101011 000111 110100

Vedremo il primo segmento a 6 bit per mostrarvi come funziona il processo di sostituzione:

111011

Dal momento che il primo numero e l’ultimo numero sono entrambi 1, questo ci dà un valore di 11. Quindi convertiamo 11 dal binario al decimale, che ci dà 3. Questi sono solo valori equivalenti, scritti in diversi modi. Pensa a come convertire il linguaggio del computer in linguaggio umano. Puoi controllare tu stesso la conversione con un calcolatore online se vuoi.

Prendiamo quindi le quattro cifre centrali del primo segmento a 6 bit:

111011

E convertili da binari a decimali. 1101 si traduce in numero 13.

Ora prendiamo questi due numeri e li cerchiamo nel S1 tavolo:

               

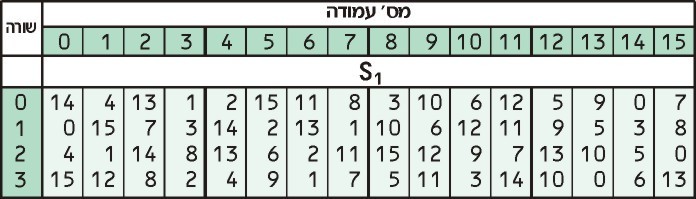
Il nostro primo numero, 3, ci dice di guardare in terza fila, mentre il nostro secondo numero, 13 ci dice di guardare nella tredicesima colonna. Il valore nella terza riga della 13a colonna è 0.

Ora che abbiamo cercato il nostro numero nella tabella, lo riconvertiamo in binario a quattro cifre. Zero è normalmente scritto come 0 in binario, ma 0000 è lo stesso e questo è il formato più adatto ai nostri scopi.

Seguendo questo processo, l’S-box converte la nostra prima sezione di dati a 6 bit (111011) in un diverso valore a 4 bit (0000). Sembra contorto, ma questa tecnica aiuta a oscurare ulteriormente la relazione tra il testo cifrato e il testo in chiaro a cui è collegato.

La successiva sezione di dati a 6 bit passa quindi attraverso lo stesso processo, ma utilizza invece la casella S2 mostrata sopra. La terza sezione utilizza la tabella S3 e così via, fino a quando la sezione finale subisce la sostituzione tramite la tabella S8.

Ancora una volta, imbrogliamo per il resto dei valori. Diciamo che le caselle di sostituzione ci danno un risultato di:

0000 1010 1100 1001 0100 1001 0111 0001

Una volta che ogni sezione dei dati è passata attraverso la sua S-box, passa al passaggio successivo.

Permutazione

L’ultimo stadio della funzione F è un’altra permutazione, usando la seguente tabella: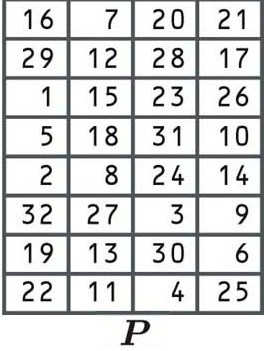

Ormai dovresti avere una buona comprensione di come le permutazioni spostano le cifre dal vecchio blocco a una posizione diversa nel nuovo blocco, quindi non ci torneremo più.

Diciamo che questa permutazione prende il nostro risultato precedente:

0000 1010 1100 1001 0100 1001 0111 0001

E ci dà un output di:

0101 0110 1001 0101 0010 0100 0101 0010

Ora che la permutazione è stata completata, abbiamo terminato con i quattro passaggi della funzione F in questo round. In notazione matematica, questo valore è noto come f (R0, K1). Ciò significa che il risultato è la funzione (f) del lato destro iniziale del blocco (R0) e della sottochiave del primo round (K1).

XOR con il blocco sinistro

Ricordi come abbiamo diviso il blocco a metà poco prima di iniziare i passaggi della funzione F? Mettiamo da parte il lato sinistro del blocco (L0), mentre il lato destro ha subito ciascuno di questi processi. Bene, ora è tempo che L0 torni in azione.

Prendiamo la parte giusta che abbiamo appena elaborato f (R0, K1) e aggiungilo al vecchio lato sinistro (L0) utilizzando il codice XOR. Questo ci dà R1, il risultato del nostro primo round:

f (R0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0:                                    1101 0111 0100 1010 1010 1000 1001 1101

Risultato XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Fare riferimento al Miscelazione chiave sopra se hai bisogno di un promemoria su come funziona il codice XOR.

Altri 15 round …

Se sei arrivato così lontano, probabilmente DES sembra un processo arduo. Ma non è nemmeno vicino al completamento. I dati vanno attraverso i quattro passaggi della funzione F, seguiti da XOR, altre 15 volte, per un totale di 16 round.

Nel secondo round, prendiamo la versione originale e non trattata del lato destro del blocco (R0) e ne facciamo il nuovo lato sinistro (L1). Nel frattempo, prendiamo il risultato del nostro primo round e lo inviamo tramite la funzione F. Tutto accade come l’ultima volta, tuttavia questa volta viene utilizzata la sottochiave per il secondo round. Diciamo che questo processo ci dà il risultato di:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Quindi XOR il risultato con L1, che in realtà è R0 (lo abbiamo derivato nel file Blocchi di scissione sezione). Questo ci dà il risultato del secondo round, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Questo passaggio può sembrare un po ‘confuso, ma secondo lo schema di Feistel, il vecchio lato destro diventa la nuova sinistra, mentre il risultato dell’operazione diventa il nuovo lato destro.

Il diagramma seguente offre una rappresentazione visiva di ciò che sta accadendo. IP rappresenta la permutazione iniziale, F è uno stand-in per l’intera funzione F, ⊕ simboleggia la funzione XOR e le frecce indicano ogni lato del blocco che si sposta tra sinistra e destra:

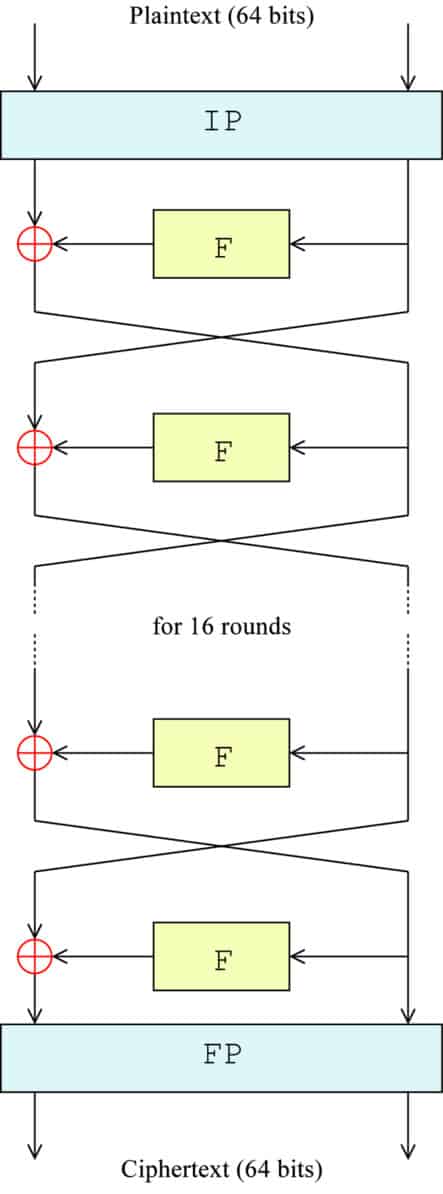
La formula esatta per ogni passaggio è:

Ln = Rn-1

Rn = Ln-1 + f(Rn-1,Kn)

Dove:

L = La metà sinistra del blocco (a partire da L0 quando il blocco è stato inizialmente diviso)

R = La metà destra del blocco (a partire da R0 quando il blocco è stato inizialmente diviso)

n = il numero tondo (che inizia con 0, quando il blocco è stato inizialmente diviso)

f = La funzione F.

Kn = la sottochiave per il round n

Secondo la formula e il diagramma, nel terzo turno, R1 diventa la nuova metà sinistra (L2), mentre R2 viene elaborato tramite la funzione F. Diciamo che ci dà un risultato di:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Quindi calcoliamo il risultato del nostro terzo round (R3), usando il codice XOR, proprio come prima:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

Lo stesso processo continua fino al quindicesimo round, con i blocchi che cambiano e la sottochiave successiva viene utilizzata in ogni round. Nel sedicesimo e ultimo round, i blocchi non vengono commutati. Invece, vengono combinati per formare un blocco a 64 bit. L’astensione dallo scambio dei blocchi in quest’ultima fase consente di utilizzare l’algoritmo sia per la crittografia che per la decrittografia.

Diciamo che il round finale ci dà il risultato di:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Permutazione finale

Questa permutazione è l’inverso della permutazione iniziale e, di nuovo, non aggiunge alcun valore di sicurezza aggiuntivo. Riorganizza i dati secondo la seguente tabella:

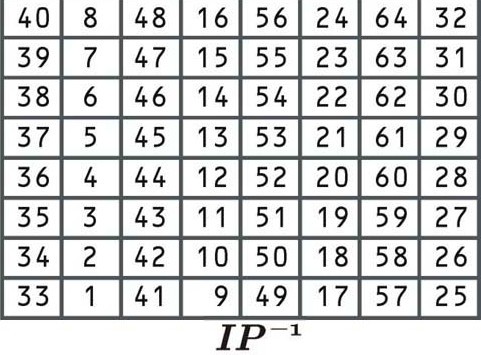
Questa tabella di permutazione funziona come le precedenti. Poiché è il passaggio finale del processo di crittografia, il risultato sarà il testo cifrato per il primo blocco di “Andiamo alla spiaggia”. Diciamo che il blocco crittografato è:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Ora, se volessi il vero testo cifrato per “Andiamo in spiaggia”, avresti potuto semplicemente saltare l’intero processo di apprendimento e passare direttamente a uno strumento di crittografia DES online. Se inseriamo la nostra frase accanto a una chiave (diciamo kj329nf982bc9wn1) lo strumento ci fornisce un testo crittografato di:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Se vuoi, puoi quindi convertire la chiave e il testo cifrato in binario e poi confrontare come il testo cifrato del primo blocco si allinea con l’intero processo che è stato delineato.

Decrittazione DES

Nel DES, il processo di decodifica è incredibilmente semplice. La struttura Feistel dell’algoritmo consente di invertire facilmente. Il processo viene eseguito quasi esattamente per decrittografare le informazioni. L’unica differenza è che le sottochiavi vengono applicate al contrario. Questa è una configurazione efficiente, perché significa che lo stesso software e hardware possono essere utilizzati sia nei processi di crittografia che di decrittografia.

Per decrittografare i dati, passa prima attraverso una permutazione iniziale, quindi il blocco viene suddiviso e la metà destra passa attraverso la funzione F. La differenza è che nel primo giro di decodifica viene applicata la 16a sottochiave. Tutto il resto procede normalmente. Una volta completata, la funzione F viene XORata con il lato sinistro del blocco.

I blocchi vengono commutati e il risultato passa attraverso lo stesso processo per il secondo round, con l’unica eccezione che viene applicata la 15 ° sottochiave. Questo processo continua fino al 16 ° round, quando viene utilizzata la prima sottochiave.

Proprio come nel processo di crittografia, i blocchi non vengono scambiati nella fase finale e quindi i dati subiscono una permutazione finale. Questo termina il processo di decodifica, risultante nel testo in chiaro originale del messaggio.

3DES

Man mano che le debolezze di sicurezza di DES sono diventate più evidenti, è stato proposto 3DES come un modo per estendere le sue dimensioni chiave senza dover costruire un algoritmo completamente nuovo. Anziché utilizzare una singola chiave come in DES, 3DES esegue l’algoritmo DES tre volte, con tre chiavi a 56 bit:

• La chiave uno è usata per cifrare il testo in chiaro.
• La chiave due è usata per decrypt il testo che era stato crittografato dalla chiave uno.
• La chiave tre è usata per cifrare il testo che è stato decifrato dalla chiave tre.

In ogni fase, il processo DES completo è seguito come indicato sopra.

Ora, ti starai chiedendo “In che modo l’applicazione della decrittazione nel secondo passaggio migliora la sicurezza?”

La risposta è che utilizza una chiave separata. Se la prima chiave fosse utilizzata anche per decrittografare i dati nel secondo passaggio, i dati sarebbero tornati da dove erano iniziati.

Tuttavia, poiché utilizza una chiave diversa, il processo di decodifica non serve effettivamente a decrittografare i dati. Può sembrare logicamente perverso, ma la decodifica con una chiave separata serve solo a confondere i dati ancora di più.

Una volta che la seconda chiave ha “decrittografato” i dati, la terza chiave viene applicata per crittografarli nuovamente. Il risultato è il testo cifrato 3DES.

3DES è strutturato in questo modo perché consente alle implementazioni di essere compatibili con DES a chiave singola, DES a due chiavi e DES a tre chiavi (illustrate nella sezione seguente). Ciò non funzionerebbe se la crittografia fosse utilizzata in tutti e tre i passaggi.

Opzioni di digitazione 3DES

Tecnicamente, 3DES può essere implementato con tre diverse configurazioni chiave. Nonostante ciò, la seconda e la terza opzione non sono sicure e non dovrebbero mai essere implementate.

• Opzione di digitazione uno – Questa opzione utilizza tre chiavi indipendenti ed è la più sicura.
• Opzione di digitazione due – In questa configurazione, la prima e la terza chiave sono uguali.
• Opzione di digitazione tre – Utilizza tre chiavi identiche. Quando vengono utilizzate chiavi identiche, il processo di decrittografia nella seconda fase annulla la prima crittografia, lasciando solo la crittografia finale per modificare i dati. Questo rende il risultato il come il normale DES.

Il processo 3DES: opzione di digitazione uno

Siamo onesti, l’intero processo 3DES può far girare la testa, soprattutto se sei nuovo nella crittografia. Per aiutarlo ad affondare, ecco un breve riassunto dell’intero schema di crittografia dell’algoritmo 3DES:

Il testo in chiaro entra nell’algoritmo 3DES ed è il primo crittografato con una chiave nei seguenti passaggi:

• • Pianificazione chiave: le 16 sottochiavi sono derivate dalla chiave uno

  • Permutazione iniziale

  • Il blocco è diviso in metà sinistra e destra

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il round

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Rendi il vecchio lato destro il nuovo lato sinistro e il risultato il nuovo lato destro

      Ripeti i passaggi precedenti 14 volte

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il sedicesimo round

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Combina insieme i lati sinistro e destro del blocco

• • Permutazione finale

Prendi il testo che è stato crittografato con la chiave uno, quindi invialo tramite Processo di “decodifica” con chiave Due:

• • Programma chiave: le 16 sottochiavi derivano dalla chiave due

  • Permutazione iniziale

  • Il blocco è diviso in metà sinistra e destra

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il round (a partire dalla 16a sottochiave per la decrittazione)

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Rendi il vecchio lato destro il nuovo lato sinistro e il risultato il nuovo lato destro

      Ripeti i passaggi precedenti 14 volte

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il primo turno

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Combina insieme i lati sinistro e destro del blocco
  • Permutazione finale

Prendi i dati che sono stati “decifrati” dalla chiave due, quindi inviali tramite il itprocesso di crittografia con chiave tre:

• • Programma chiave: le 16 sottochiavi derivano dalla chiave tre

  • Permutazione iniziale

  • Il blocco è diviso in metà sinistra e destra

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il round

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Rendi il vecchio lato destro il nuovo lato sinistro e il risultato il nuovo lato destro

      Ripeti i passaggi precedenti 14 volte

• • • La metà destra viene inviata tramite la funzione F.

      • Permutazione di espansione

      • XOR con la sottochiave per il sedicesimo round

      • Sostituzione

      • Permutazione

    • XOR il risultato della funzione F con il lato sinistro

    • Combina insieme i lati sinistro e destro del blocco

• • Permutazione finale

Il risultato è il testo cifrato 3DES.

La sicurezza di 3DES

La sicurezza di 3DES dipende dall’opzione di codifica utilizzata. L’opzione di codifica uno prevede tre diverse chiavi a 56 bit, che forniscono una lunghezza totale della chiave di 168 bit. La lunghezza effettiva è ridotta considerevolmente dagli attacchi meet-in-the-middle, che riducono la sicurezza del mondo reale a 112 bit.

Gli attacchi Meet-in-the-middle sono utili contro gli schemi di crittografia che ripetono lo stesso algoritmo più volte. La tecnica memorizza i valori immediati di ogni fase di crittografia, quindi utilizza queste informazioni per migliorare radicalmente il tempo necessario per forzare brutalmente l’algoritmo.

Le opzioni due e tre hanno chiavi significativamente più piccole e sono vulnerabili sia agli attacchi noti in chiaro e scelti in chiaro, sia ad altri.

Gli attacchi noti in chiaro sono possibili quando un avversario ha accesso sia al testo in chiaro che al testo cifrato di un messaggio. Se un algoritmo è sensibile a questi attacchi, l’utente malintenzionato può utilizzare queste informazioni per dedurre la chiave, che consente loro di craccare tutti gli altri dati che sono stati crittografati dalla stessa chiave.

Un attacco con testo in chiaro scelto è simile, ma coinvolge l’attaccante che scopre la chiave confrontando i cifrati con quelli in chiaro.

A causa di queste vulnerabilità e delle piccole dimensioni complessive delle chiavi coinvolte, le opzioni di codifica due e tre non sono sicure e non dovrebbero essere implementate.

3DES è sicuro?

Poiché 3DES sarà deprecato nei prossimi anni, è meglio usare altri algoritmi. Mentre l’opzione di digitazione uno è ancora considerata sicura per molte applicazioni, non ci sono molte buone ragioni per cui dovrebbe essere usata al posto di un’alternativa come AES.

Sebbene 3DES occupi un posto importante nella crittografia come follow-up di DES, i suoi anni di gloria sono finiti ed è tempo di andare avanti. Se vuoi proteggere i tuoi sistemi in futuro, dovresti invece utilizzare un algoritmo più aggiornato.

Relazionato: Spiegazione dei tipi di crittografia comuni

Plan X da DoD autorizzato sotto CC0