Was ist der Diffie-Hellman-Schlüsselaustausch und wie funktioniert er?

Der Diffie-Hellman-Schlüsselaustausch war eine der wichtigsten Entwicklungen in der Public-Key-Kryptographie und es wird immer noch häufig in einer Reihe von heutigen verschiedenen Sicherheitsprotokollen implementiert.

Es ermöglicht zwei Parteien, die sich zuvor noch nicht getroffen haben, einen sicheren Schlüssel zu erstellen, mit dem sie ihre Kommunikation sichern können. In diesem Artikel erklären wir Schritt für Schritt, wofür es verwendet wird, wie es funktioniert, welche Variationen es gibt und welche Sicherheitsaspekte beachtet werden müssen, um es sicher zu implementieren.

Was ist der Diffie-Hellman-Schlüsselaustausch??

Der Diffie-Hellman-Schlüsselaustausch war der erste weit verbreitete Methode zum sicheren Entwickeln und Austauschen von Schlüsseln über einen unsicheren Kanal.

In den obigen Begriffen mag es nicht so aufregend oder bahnbrechend erscheinen. Lassen Sie uns ein Beispiel geben, das erklärt, warum der Diffie-Hellman-Schlüsselaustausch ein so wichtiger Meilenstein in der Welt der Kryptografie war und warum er bis heute so häufig verwendet wird.

Nehmen wir an, Sie sind ein streng geheimer Spion und müssen einige wichtige Informationen an Ihr Hauptquartier senden. Wie würden Sie Ihre Feinde daran hindern, von der Botschaft Kenntnis zu nehmen??

Die häufigste Lösung wäre, die Nachricht mit einem Code zu verschlüsseln. Am einfachsten ist es, die Art des Codes und Schlüssels, die Sie verwenden möchten, vorher zu vereinbaren oder über einen sicheren Kommunikationskanal zu erledigen.

Nehmen wir an, Sie sind ein besonders schlechter Spion, und Sie und Ihr Hauptquartier entscheiden sich für die Verschlüsselung Ihrer Nachrichten mit einer schwachen Shift-Chiffre. In diesem Code wird jedes “a” zu “b”, jedes “b” wird zu “c”, jedes “c” wird zu “d” und so weiter, bis das “z” zu einem “a” wird..

Unter dieser Shift-Chiffre wird die Meldung “Let’s get dinner” zu “Mfu’t hfu ejoofs”. Zum Glück sind Ihre Gegner in unserer hypothetischen Situation genauso inkompetent wie Sie und können einen so einfachen Code nicht knacken, dass sie nicht auf den Inhalt der Nachricht zugreifen können.

Aber was passiert, wenn Sie zuvor keinen Code mit Ihrem Empfänger vereinbaren konnten??

Nehmen wir an, Sie möchten mit einem Spion einer verbündeten Nation kommunizieren, den Sie noch nie zuvor getroffen haben. Sie haben keinen sicheren Kanal, über den Sie mit ihnen sprechen können. Wenn Sie Ihre Nachricht nicht verschlüsseln, kann jeder Gegner, der sie abfängt, den Inhalt lesen. Wenn Sie es verschlüsseln, ohne dem Verbündeten den Code mitzuteilen, kann der Feind es nicht lesen, der Verbündete jedoch auch nicht.

Dieses Problem war bis in die 1970er Jahre eines der größten Rätsel in der Kryptographie:

Wie können Sie sicher Informationen mit jemandem austauschen, wenn Sie nicht die Möglichkeit hatten, den Schlüssel im Voraus zu teilen??

Der Diffie-Hellman-Schlüsselaustausch war der erste öffentlich genutzte Mechanismus zur Lösung dieses Problems. Der Algorithmus ermöglicht es denjenigen, die sich noch nie zuvor getroffen haben, einen gemeinsamen Schlüssel sicher zu erstellen, selbst über einen unsicheren Kanal, den Gegner möglicherweise überwachen.

Die Geschichte des Diffie-Hellman-Schlüsselaustauschs

Der Diffie-Hellman-Schlüsselaustausch geht auf die 1970er Jahre zurück. Während sich das Gebiet der Kryptographie zu Beginn des 20. Jahrhunderts erheblich entwickelt hatte, konzentrierten sich diese Fortschritte hauptsächlich auf das Gebiet der Kryptographie mit symmetrischen Schlüsseln.

Erst 1976 tauchten Algorithmen mit öffentlichem Schlüssel im öffentlichen Raum auf, als Whitfield Diffie und Martin Hellman ihre Arbeit veröffentlichten, Neue Wege in der Kryptographie. Die Zusammenarbeit skizzierte die Mechanismen hinter einem neuen System, das als das bekannt werden würde Diffie-Hellman-Schlüsselaustausch.

Die Arbeit wurde teilweise von früheren Entwicklungen von Ralph Merkle inspiriert. Die sogenannte Merkles Rätsel Dazu muss eine Partei eine Reihe von kryptografischen Rätseln erstellen und an die andere senden. Diese Rätsel würden eine moderate Menge an Rechenressourcen erfordern, um gelöst zu werden.

Der Empfänger wählt nach dem Zufallsprinzip ein zu lösendes Rätsel aus und unternimmt den erforderlichen Aufwand, um es zu lösen. Sobald das Rätsel gelöst ist, werden dem Empfänger eine Kennung und ein Sitzungsschlüssel angezeigt. Der Empfänger sendet dann die Kennung zurück an den ursprünglichen Absender, wodurch der Absender weiß, welches Rätsel gelöst wurde.

Da der ursprüngliche Absender die Rätsel erstellt hat, gibt der Bezeichner an, welchen Sitzungsschlüssel der Empfänger gefunden hat, und die beiden Parteien können diesen Schlüssel verwenden, um sicherer zu kommunizieren. Wenn ein Angreifer die Interaktion mithört, hat er Zugriff auf alle Rätsel sowie auf die Kennung, die der Empfänger an den ursprünglichen Absender zurücksendet.

Die ID sagt dem Angreifer nicht, welcher Sitzungsschlüssel verwendet wird. Der beste Ansatz zum Entschlüsseln der Informationen ist daher, Löse alle Rätsel, um den richtigen Sitzungsschlüssel zu finden. Da der Angreifer im Durchschnitt die Hälfte der Rätsel lösen muss, ist es für ihn viel schwieriger, den Schlüssel zu finden, als für den Empfänger.

Dieser Ansatz bietet mehr Sicherheit, ist jedoch keine perfekte Lösung. Der Diffie-Hellman-Schlüsselaustausch nahm einige dieser Ideen auf und machte sie komplexer, um eine sichere Methode für die Kryptographie mit öffentlichen Schlüsseln zu schaffen.

Martin Hellman hat vorgeschlagen, den Algorithmus stattdessen als Diffie-Hellman-Merkle-Schlüsselaustausch zu bezeichnen, um die Arbeit von Ralph Merkle im Bereich der Kryptographie mit öffentlichen Schlüsseln widerzuspiegeln.

Es wurde öffentlich angenommen, dass Merkle, Hellman und Diffie die ersten Leute waren, die die Kryptographie mit öffentlichen Schlüsseln entwickelten, bis 1997 die britische Regierung Arbeiten, die Anfang der 1970er Jahre von Merkle, Hellman und Diffie durchgeführt wurden, deklassierte James Ellis, Clifford Cox und Malcolm Williamson.

Es stellte sich heraus, dass das Trio zwischen 1969 und 1973 das erste Public-Key-Verschlüsselungsschema entwickelte, dessen Arbeit jedoch für zwei Jahrzehnte klassifiziert war. Es wurde unter dem Government Communication Headquarters (GCHQ), einem britischen Geheimdienst, durchgeführt.

Ihre Entdeckung war der RSA-Algorithmus. Diffie, Hellman und Merkle waren also noch die ersten, die den Diffie-Hellman-Schlüsselaustausch entwickelten, aber nicht mehr die ersten Erfinder der Public-Key-Kryptographie.

Wo wird der Diffie-Hellman-Schlüsselaustausch verwendet??

Der Hauptzweck des Diffie-Hellman-Schlüsselaustauschs ist: Entwickeln Sie auf sichere Weise gemeinsame Geheimnisse, die zum Ableiten von Schlüsseln verwendet werden können. Diese Schlüssel können dann mit Algorithmen für symmetrische Schlüssel verwendet werden, um Informationen auf geschützte Weise zu übertragen. Symmetrische Algorithmen werden in der Regel verwendet, um den Großteil der Daten zu verschlüsseln, da sie effizienter sind als Algorithmen mit öffentlichem Schlüssel.

Technisch kann der Diffie-Hellman-Schlüsselaustausch verwendet werden, um öffentliche und private Schlüssel herzustellen. In der Praxis wird jedoch eher RSA verwendet. Dies liegt daran, dass der RSA-Algorithmus auch Public-Key-Zertifikate signieren kann, der Diffie-Hellman-Schlüsselaustausch jedoch nicht.

Der in PGP häufig verwendete ElGamal-Algorithmus basiert auf dem Diffie-Hellman-Schlüsselaustausch. Jedes Protokoll, das diesen Algorithmus verwendet, implementiert also eine Art Diffie-Hellman.

Als eine der gebräuchlichsten Methoden zur sicheren Verteilung von Schlüsseln gilt der Diffie-Hellman-Schlüsselaustausch häufig in Sicherheitsprotokollen wie TLS, IPsec, SSH, PGP und vielen anderen implementiert. Dies macht es zu einem integralen Bestandteil unserer sicheren Kommunikation.

Im Rahmen dieser Protokolle wird der Diffie-Hellman-Schlüsselaustausch häufig verwendet, um die Verbindung zu einer Website zu sichern, auf einen anderen Computer remote zuzugreifen und verschlüsselte E-Mails zu senden

Wie funktioniert der Diffie-Hellman-Schlüsselaustausch??

Der Diffie-Hellman-Schlüsselaustausch ist komplex und es kann schwierig sein, sich ein Bild davon zu machen, wie er funktioniert. Es verwendet sehr große Zahlen und viel Mathematik, Etwas, das viele von uns immer noch aus diesen langen und langweiligen High-School-Stunden scheuen.

Zum leichteren Verständnis, Wir beginnen damit, den Diffie-Hellman-Schlüsselaustausch mit einer Analogie zu erklären. Sobald Sie eine umfassende Vorstellung davon haben, wie es funktioniert, werden wir die zugrunde liegenden Prozesse genauer beschreiben.

Die beste Analogie für das Diffie-Hellman-Schema ist zu denken zwei Leute mischen Farbe. Verwenden wir den Kryptografiestandard und sagen, dass sie Alice und Bob heißen. Zunächst einigen sich beide auf eine zufällige Farbe. Nehmen wir an, dass sie sich gegenseitig eine Nachricht senden und Entscheiden Sie sich für Gelb als gemeinsame Farbe, Genau wie im Diagramm unten:

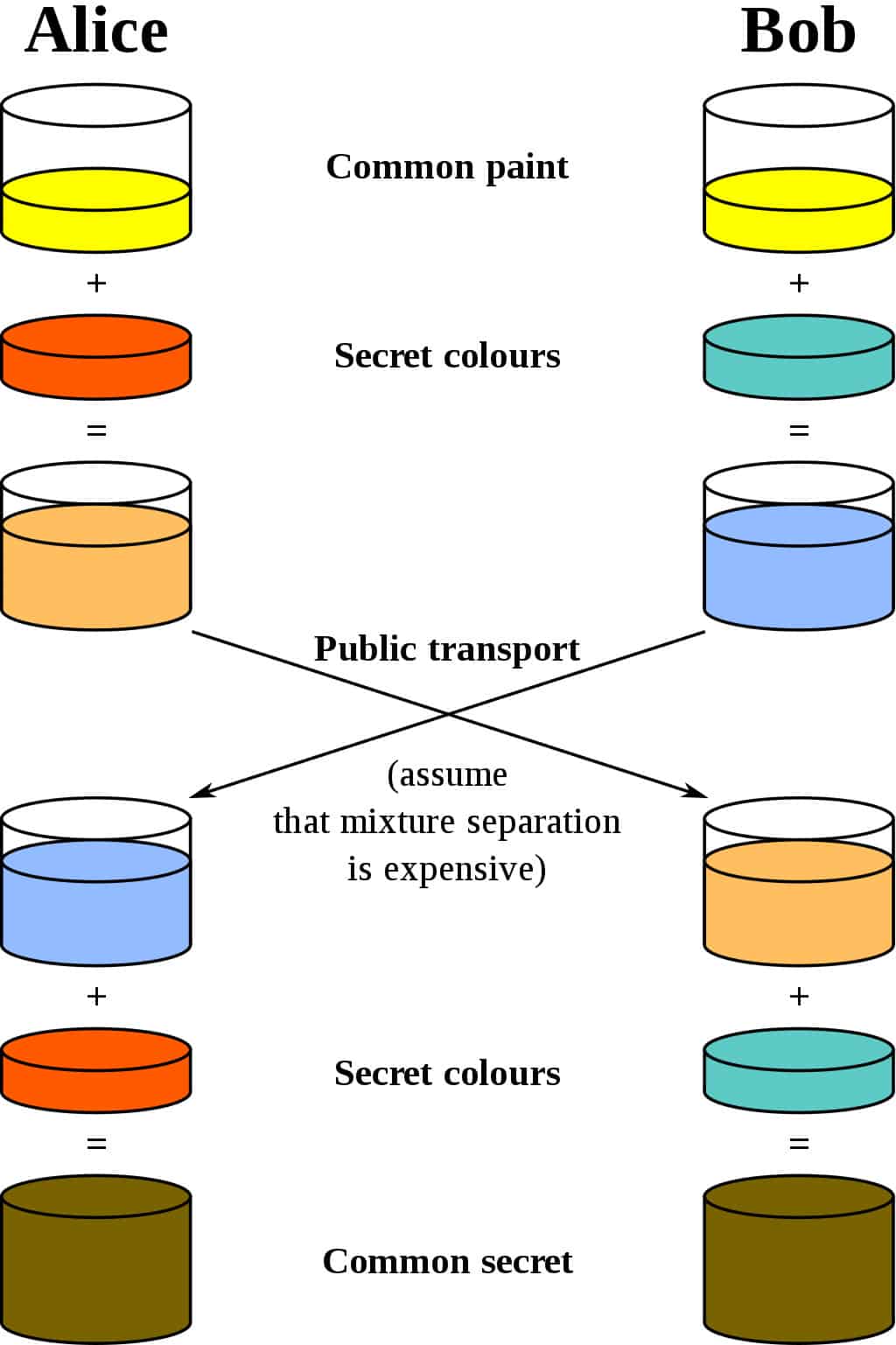
se ihre eigene geheime Farbe. Sie teilen der anderen Partei ihre Wahl nicht mit. Nehmen wir an, Alice wählt rot, während Bob a wählt leicht grünlich blau.

Der nächste Schritt ist, dass sowohl Alice als auch Bob ihre geheime Farbe (rot für Alice, grün-blau für Bob) mit dem Gelb mischen, auf das sie sich einig waren. Nach dem Diagramm endet Alice mit einem orangish mix, während Bobs Ergebnis a ist tieferes blau.

Sobald sie das Mischen beendet haben, senden sie das Ergebnis an die andere Partei. Alice erhält das tiefere Blau, während Bob wird die orangefarbene Farbe geschickt.

Sobald sie das gemischte Ergebnis von ihrem Partner erhalten haben, fügen sie ihm ihre geheime Farbe hinzu. Alice nimmt das tiefere Blau und fügt ihre geheime rote Farbe hinzu, während Bob fügt sein geheimes Grün-Blau zu der Orange-Mischung hinzu, die er gerade erhalten hat.

Das Ergebnis? Sie haben beide die gleiche Farbe, was in diesem Fall ein ekelhaftes Braun ist. Es ist vielleicht nicht die Farbe, mit der Sie Ihr Wohnzimmer streichen möchten, aber es ist trotzdem eine gemeinsame Farbe. Diese gemeinsame Farbe wird als. Bezeichnet gemeinsames Geheimnis.

Der entscheidende Teil des Diffie-Hellman-Schlüsselaustauschs besteht darin, dass beide Parteien dasselbe Ergebnis erzielen, ohne jemals das gesamte gemeinsame Geheimnis über den Kommunikationskanal senden zu müssen. Die Wahl einer gemeinsamen Farbe, ihrer eigenen geheimen Farben, das Austauschen der Mischung und das erneute Hinzufügen ihrer eigenen Farbe geben beiden Parteien die Möglichkeit, zu demselben gemeinsamen Geheimnis zu gelangen, ohne jemals die ganze Sache übermitteln zu müssen.

Wenn ein Angreifer den Austausch abhört, kann er nur auf die gemeinsame gelbe Farbe zugreifen, mit der Alice und Bob beginnen, sowie auf die gemischten Farben, die ausgetauscht werden. Da wird dies wirklich mit enormen Stückzahlen statt mit Farbe gemacht, Diese Informationen reichen für den Angriff nicht aus, um entweder die ursprüngliche geheime Farbe oder das gemeinsame Geheimnis zu erkennen (Technisch ist es möglich, das gemeinsame Geheimnis aus diesen Informationen zu berechnen, aber bei einer sicheren Implementierung des Diffie-Hellman-Schlüsselaustauschs würde dies unvorstellbar viel Zeit und Rechenressourcen in Anspruch nehmen.).

Diese Struktur des Diffie-Hellman-Schlüsselaustauschs macht ihn so nützlich. Es ermöglicht den beiden Parteien, über eine potenziell gefährliche Verbindung zu kommunizieren und dennoch ein gemeinsames Geheimnis zu entwickeln, mit dem sie Verschlüsselungsschlüssel für ihre zukünftige Kommunikation erstellen können. Es spielt keine Rolle, ob Angreifer mithören, da das gesamte gemeinsame Geheimnis niemals über die Verbindung gesendet wird.

Die technischen Details des Diffie-Hellman-Schlüsselaustauschs

Zeit für ein bisschen Mathe…

Keine Sorge, wir werden es langsam angehen und versuchen, den gesamten Prozess so einfach wie möglich zu gestalten. Es folgt einer ähnlichen Prämisse wie die oben gezeigte Analogie, aber anstatt Farben zu mischen und zu senden, Das Diffie-Hellman-Schema führt tatsächlich Berechnungen aus, die auf außergewöhnlich großen Primzahlen basieren, und sendet sie dann weiter.

Um die Sicherheit zu gewährleisten, wird empfohlen, die prime (p) ist mindestens 2048 Bit lang, Das ist das binäre Äquivalent einer Dezimalzahl von ungefähr dieser Größe:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

Damit niemandem der Kopf explodiert, werden wir diese Erklärung mit viel kleineren Zahlen durchgehen. Beachten Sie, dass Der Diffie-Hellman-Schlüsselaustausch wäre unsicher, wenn er Zahlen verwendet, die so klein sind wie die in unserem Beispiel. Wir verwenden nur so kleine Zahlen, um das Konzept auf einfachere Weise zu demonstrieren.

In der einfachsten Form des Diffie-Hellman-Schlüsselaustauschs, Alice und Bob entscheiden sich zunächst gegenseitig für zwei Zahlen, im Gegensatz zu der einzigen gemeinsamen Farbe im obigen Beispiel. Diese sind der Modul (p) und die Basis (G).

Im praktischen Einsatz, der Modul (p) ist eine sehr große Primzahl, während die Basis (G) ist relativ klein, um die Berechnungen zu vereinfachen. Die Basis (G) leitet sich von einer zyklischen Gruppe ab (G), die normalerweise generiert wird, bevor die anderen Schritte stattfinden.

Nehmen wir für unser Beispiel an, dass der Modul (p) ist 17, während die Basis (G) ist 4.

Sobald sie sich gegenseitig auf diese Nummern festgelegt haben, legt Alice eine Geheimnummer fest (ein) für sich selbst, während Bob seine eigene Geheimnummer wählt (b). Nehmen wir an, sie wählen:

a = 3

b = 6

Alice führt dann die folgende Berechnung durch, um ihr die Nummer zu geben, die sie an Bob senden wird:

A = ga mod p

In der obigen Berechnung, mod bezeichnet eine Modulo-Operation. Dies sind im Wesentlichen Berechnungen, um den Rest nach dem Teilen der linken Seite durch die rechte herauszufinden. Als Beispiel:

15 mod 4 = 3

Wenn Sie wissen, wie Modulo-Operationen funktionieren, können Sie diese in den folgenden Berechnungen selbst ausführen. Andernfalls können Sie einen Online-Rechner verwenden.

Lassen Sie uns also unsere Zahlen in die Formel einfügen:

A = 43 mod 17

A = 64 mod 17

A = 13

Wenn wir dasselbe für Bob tun, erhalten wir:

B = 46 mod 17

B = 4096 mod 17

B = 16

Alice schickt dann ihr Ergebnis (EIN) an Bob, während Bob seine Figur schickt (B) zu Alice. Alice berechnet dann das gemeinsame Geheimnis (s) unter Verwendung der Nummer, die sie von Bob erhalten hat (B) und ihre Geheimnummer (ein) nach folgender Formel:

s = Ba mod p

s = 163 mod 17

s = 4.096 mod 17

s = 16

Bob führt dann im Wesentlichen die gleiche Berechnung durch, jedoch mit der Zahl, die Alice ihm gesendet hat (EIN) sowie seine eigene Geheimnummer (b):

s = EINb mod p

s = 136 mod 17

s = 4.826.809 mod 17

s = 16

Wie Sie sehen, endeten beide Parteien mit dem gleichen Ergebnis für s, 16. Dies ist das gemeinsame Geheimnis, das nur Alice und Bob kennen. Auf diese Weise können sie einen Schlüssel für die symmetrische Verschlüsselung einrichten und Informationen sicher untereinander senden, so dass nur sie darauf zugreifen können.

Beachten Sie, dass obwohl B und s Dies ist nur ein Zufall, der auf den kleinen Zahlen basiert, die für diese Abbildung ausgewählt wurden. Normalerweise stimmen diese Werte in einer realen Implementierung des Diffie-Hellman-Schlüsselaustauschs nicht überein.

Obwohl viele der oben genannten Daten im Klartext über den Kanal gesendet werden (p, g, A und B) und kann von potentiellen Angreifern gelesen werden, die das gemeinsame Geheimnis (s) wird niemals übertragen. Es wäre für einen Angreifer nicht praktisch, das gemeinsame Geheimnis zu berechnen (s) oder eine der Geheimnummern (ein und b) aus den Informationen, die im Klartext gesendet werden.

Dies setzt natürlich voraus, dass der Diffie-Hellman-Schlüsselaustausch ordnungsgemäß implementiert ist und ausreichend große Zahlen verwendet werden. Solange diese Bestimmungen eingehalten werden, wird der Diffie-Hellman-Schlüsselaustausch als sicherer Weg angesehen, um ein gemeinsames Geheimnis zu etablieren, das zur Sicherung der zukünftigen Kommunikation verwendet werden kann.

Erstellen eines gemeinsamen Schlüssels zwischen mehreren Parteien

Der Diffie-Hellman-Schlüsselaustausch kann auch verwendet werden, um einen gemeinsamen Schlüssel mit einer größeren Anzahl von Teilnehmern einzurichten. Dies funktioniert auf die gleiche Weise, mit der Ausnahme, dass weitere Runden der Berechnungen erforderlich sind, damit jede Partei ihre Geheimzahl hinzufügt und dasselbe gemeinsame Geheimnis erhält.

Genau wie in der Zwei-Parteien-Version des Diffie-Hellman-Schlüsselaustauschs werden einige Teile der Informationen über unsichere Kanäle gesendet, aber nicht genug, damit ein Angreifer das gemeinsame Geheimnis berechnen kann.

Warum ist der Diffie-Hellman-Schlüsselaustausch sicher??

Auf mathematischer Ebene stützt sich der Diffie-Hellman-Schlüsselaustausch auf Einwegfunktionen als Grundlage für seine Sicherheit. Dies sind Berechnungen, die einfach in eine Richtung durchgeführt werden können, aber viel schwieriger in umgekehrter Richtung zu berechnen sind.

Insbesondere stützt es sich auf das Diffie-Hellman-Problem, bei dem davon ausgegangen wird, dass es unter den richtigen Parametern nicht möglich ist, zu berechnen Gab aus den separaten Werten von G, Gein und Gb. Es gibt derzeit keinen öffentlich bekannten Weg, um leicht zu finden Gab Aus diesem Grund wird der Diffie-Hellman-Schlüsselaustausch als sicher angesehen, obwohl Angreifer die Werte abfangen können p, G, EIN, und B.

Authentifizierung & der Diffie-Hellman-Schlüsselaustausch

In der realen Welt wird der Diffie-Hellman-Schlüsselaustausch nur selten alleine verwendet. Der Hauptgrund dafür ist, dass Es bietet keine Authentifizierung, sodass Benutzer für Man-in-the-Middle-Angriffe anfällig sind.

Diese Angriffe können stattfinden, wenn der Diffie-Hellman-Schlüsselaustausch von selbst implementiert wird Es gibt keine Möglichkeit zu überprüfen, ob die andere Partei in einer Verbindung wirklich der ist, von dem sie sagt, dass sie es ist. Ohne jegliche Authentifizierung, Benutzer können sich tatsächlich mit Angreifern verbinden wenn sie glauben, mit einer vertrauenswürdigen Partei zu kommunizieren.

Aus diesem Grund wird der Diffie-Hellman-Schlüsselaustausch im Allgemeinen zusammen mit einigen Authentifizierungsmitteln implementiert. Dabei werden häufig digitale Zertifikate und ein Public-Key-Algorithmus wie RSA verwendet, um die Identität der einzelnen Parteien zu überprüfen.

Variationen des Diffie-Hellman-Schlüsselaustauschs

Der Diffie-Hellman-Schlüsselaustausch kann auf verschiedene Arten implementiert werden und hat auch die Basis für mehrere andere Algorithmen geliefert. Einige dieser Implementierungen stellen eine Autorisierung bereit, während andere verschiedene kryptografische Merkmale aufweisen, wie z.

Elliptische Kurve Diffie-Hellman

Elliptische Kurve Diffie-Hellman nutzt die algebraische Struktur elliptischer Kurven, um mit ihren Implementierungen ein ähnliches Sicherheitsniveau mit einer kleineren Schlüsselgröße zu erreichen. Ein 224-Bit-Ellipsenkurvenschlüssel bietet die gleiche Sicherheit wie ein 2048-Bit-RSA-Schlüssel. Dies kann den Austausch effizienter gestalten und den Speicherbedarf verringern.

Abgesehen von der geringeren Schlüssellänge und der Tatsache, dass sie von den Eigenschaften elliptischer Kurven abhängt, arbeitet Diffie-Hellman mit elliptischen Kurven auf ähnliche Weise wie der standardmäßige Diffie-Hellman-Schlüsselaustausch.

TLS   

TLS, ein Protokoll, mit dem ein Großteil des Internets gesichert wird, kann den Diffie-Hellman-Austausch auf drei verschiedene Arten nutzen: anonym, statisch und kurzlebig. In der Praxis sollte nur kurzlebiges Diffie-Hellman implementiert werden, da die anderen Optionen Sicherheitsprobleme aufweisen.

• Anonymes Diffie-Hellman – Diese Version des Diffie-Hellman-Schlüsselaustauschs verwendet keine Authentifizierung und ist daher für Man-in-the-Middle-Angriffe anfällig. Es sollte nicht verwendet oder implementiert werden.
• Statischer Diffie-Hellman – Static Diffie-Hellman verwendet Zertifikate zur Authentifizierung des Servers. Der Client wird nicht standardmäßig authentifiziert und es wird auch keine Vorwärtsgeheimnis bereitgestellt.
• Vergänglicher Diffie-Hellman – Dies wird als die sicherste Implementierung angesehen, da sie eine perfekte Vorwärtsgeheimnis bietet. Es wird im Allgemeinen mit einem Algorithmus wie DSA oder RSA kombiniert, um eine oder beide Parteien in der Verbindung zu authentifizieren. Ephemeral Diffie-Hellman verwendet jedes Mal, wenn das Protokoll ausgeführt wird, unterschiedliche Schlüsselpaare. Auf diese Weise wird die Verbindung perfekt für die Weiterleitung geschützt, da ein zukünftig kompromittierter Schlüssel nicht zum Entschlüsseln aller früheren Nachrichten verwendet werden kann.

ElGamal

ElGamal ist ein Algorithmus für öffentliche Schlüssel, der auf dem Diffie-Hellman-Schlüsselaustausch aufbaut. Wie Diffie-Hellman enthält es keine Bestimmungen für die eigene Authentifizierung und wird in der Regel mit anderen Mechanismen für diesen Zweck kombiniert.

ElGamal wurde hauptsächlich in PGP, GNU Privacy Guard und anderen Systemen verwendet, da sein Hauptkonkurrent RSA patentiert wurde. Das RSA-Patent lief im Jahr 2000 aus, so dass es nach diesem Datum frei eingeführt werden konnte. Seitdem wurde ElGamal nicht mehr so ​​häufig implementiert.

STS

Das STS-Protokoll (Station-to-Station) basiert ebenfalls auf dem Diffie-Hellman-Schlüsselaustausch. Es ist ein weiteres wichtiges Vertragsschema, bietet jedoch Schutz vor Man-in-the-Middle-Angriffen sowie perfekte Geheimhaltung für die Zukunft.

Es erfordert, dass beide Parteien in der Verbindung bereits ein Schlüsselpaar haben, das zur Authentifizierung jeder Seite verwendet wird. Wenn die Parteien sich nicht bereits bekannt sind, können Zertifikate verwendet werden, um die Identität beider Parteien zu validieren.

Der Diffie-Hellman-Schlüsselaustausch & RSA

Wie wir vorher besprochen haben, Der Diffie-Hellman-Schlüsselaustausch wird häufig zusammen mit RSA oder anderen Algorithmen implementiert, um die Authentifizierung für die Verbindung bereitzustellen. Wenn Sie mit RSA vertraut sind, wundern Sie sich vielleicht Warum sollte sich jemand die Mühe machen, auch den Diffie-Hellman-Schlüsselaustausch zu verwenden?, da RSA es Parteien ermöglicht, die sich noch nie zuvor getroffen haben, sicher zu kommunizieren.

RSA ermöglicht seinen Benutzern, Nachrichten mit dem öffentlichen Schlüssel ihres Korrespondenten zu verschlüsseln, sodass sie nur mit dem passenden privaten Schlüssel entschlüsselt werden können. In der Praxis jedoch, RSA wird nicht zum Verschlüsseln der gesamten Kommunikation verwendet – dies wäre viel zu ineffizient.

Stattdessen wird RSA häufig nur zur Authentifizierung beider Parteien verwendet. Das macht es mit die digitalen Zertifikate jeder Partei, die von einer Zertifizierungsstelle überprüft wurden um zu beweisen, dass ein Zertifikatsinhaber wirklich der ist, für den er sich ausgibt, und dass der öffentliche Schlüssel auf dem Zertifikat tatsächlich ihm gehört.

Zur gegenseitigen Authentifizierung, Jeder Teilnehmer signiert eine Nachricht mit seinem privaten Schlüssel und sendet sie dann an seinen Kommunikationspartner. Jeder Empfänger kann dann Überprüfen Sie die Identität des anderen Teilnehmers, indem Sie die signierten Nachrichten mit dem öffentlichen Schlüssel auf dem digitalen Zertifikat seines Kommunikationspartners abgleichen (In dem oben genannten Artikel über RSA finden Sie weitere Einzelheiten zur Funktionsweise, insbesondere der Nachrichten signieren Sektion).

Nachdem beide Parteien authentifiziert wurden, ist es technisch möglich, RSA weiterhin zu verwenden, um sicher verschlüsselte Nachrichten zwischen ihnen zu senden. Dies wäre jedoch zu ineffizient.

Um diese Ineffizienz zu umgehen, verwenden viele Sicherheitsprotokolle einen Algorithmus wie z Der Diffie-Hellman-Schlüsselaustausch liefert ein gemeinsames Geheimnis, mit dem ein gemeinsamer symmetrischer Schlüssel erstellt werden kann. Dieser symmetrische Schlüssel wird dann in einem Algorithmus mit symmetrischem Schlüssel wie AES verwendet, um die Daten zu verschlüsseln dass die beiden Parteien beabsichtigen, sicher zwischen sich zu senden.

Es mag wie ein komplexer und komplizierter Prozess erscheinen, aber es ist am Ende viel schneller und erfordert weniger Ressourcen als die Verwendung eines Algorithmus mit öffentlichem Schlüssel für den gesamten Austausch. Das ist weil Die Verschlüsselung mit symmetrischen Schlüsseln ist um Größenordnungen effizienter als die Verschlüsselung mit öffentlichen Schlüsseln.

Zusätzlich zu den oben erwähnten Ineffizienzen gibt es einige andere Nachteile, die sich aus der ausschließlichen Verwendung von RSA ergeben würden. RSA benötigt eine Polsterung, um sicher zu sein, Daher müsste ein zusätzlicher Algorithmus entsprechend implementiert werden, um die Sicherheit zu gewährleisten.

RSA bietet keine perfekte Geheimhaltung für die Weiterleitung, Dies ist ein weiterer Nachteil im Vergleich zum kurzlebigen Diffie-Hellman-Schlüsselaustausch. Aus diesen Gründen ist es in vielen Situationen am besten, RSA nur in Verbindung mit dem Diffie-Hellman-Schlüsselaustausch anzuwenden.

Alternativ kann der Diffie-Hellman-Schlüsselaustausch mit einem Algorithmus wie dem Digital Signature Standard (DSS) kombiniert werden, um Authentifizierung, Schlüsselaustausch, Vertraulichkeit und Integrität der Daten zu gewährleisten. In einer solchen Situation ist RSA nicht erforderlich, um die Verbindung zu sichern.

Sicherheitsprobleme beim Diffie-Hellman-Schlüsselaustausch

Die Sicherheit des Diffie-Hellman-Schlüsselaustauschs hängt davon ab, wie er implementiert ist und welche Nummern für ihn ausgewählt wurden. Wie oben erwähnt, hat es keine Möglichkeit, die andere Partei selbst zu authentifizieren, aber in der Praxis werden andere Mechanismen verwendet, um sicherzustellen, dass die andere Partei in einer Verbindung kein Betrüger ist.

Parameter für die Nummernauswahl

Wenn eine reale Implementierung des Diffie-Hellman-Schlüsselaustauschs Zahlen verwendet, die so klein sind wie die in unserem Beispiel, würde dies den Austauschprozess für einen Angreifer trivial machen. Es kommt aber nicht nur auf die Größe der Zahlen an, sondern die Zahlen müssen auch ausreichend zufällig sein. Wenn ein Zufallszahlengenerator eine vorhersagbare Ausgabe erzeugt, kann dies die Sicherheit des Diffie-Hellman-Schlüsselaustauschs vollständig beeinträchtigen.

Die Nummer p sollte 2048 Bits lang sein um die Sicherheit zu gewährleisten. Die Basis, G, kann eine relativ kleine Zahl wie 2 sein, aber es muss von einer Ordnung von kommen G Das hat einen großen Primfaktor

Der Logjam-Angriff

Der Diffie-Hellman-Schlüsselaustausch wurde auf der Grundlage des schwer zu lösenden Problems des diskreten Logarithmus entwickelt. Der wirksamste öffentlich bekannte Mechanismus zum Finden der Lösung ist der Zahlenfeldsiebalgorithmus.

Die Fähigkeiten dieses Algorithmus wurden beim Entwurf des Diffie-Hellman-Schlüsselaustauschs berücksichtigt. Bis 1992 war bekannt, dass für eine bestimmte Gruppe, G, Drei der vier Schritte, die an dem Algorithmus beteiligt sind, könnten möglicherweise im Voraus berechnet werden. Wenn dieser Fortschritt gespeichert würde, könnte der letzte Schritt in vergleichsweise kurzer Zeit berechnet werden.

Dies war nicht allzu beunruhigend, bis erkannt wurde, dass ein erheblicher Teil des Internetverkehrs dieselben Gruppen verwendet, die 1024 Bit oder kleiner sind. 2015 führte ein akademisches Team die Berechnungen für die gängigsten 512-Bit-Primzahlen durch, die vom Diffie-Hellman-Schlüsselaustausch in TLS verwendet werden.

Sie konnten auch 80% der TLS-Server, die DHE-EXPORT unterstützen, downgraden, sodass sie einen exportfähigen 512-Bit-Diffie-Hellman-Schlüsselaustausch für die Verbindung akzeptierten. Das bedeutet, dass Jeder dieser Server ist anfällig für Angriffe eines gut ausgestatteten Gegners.

Die Forscher extrapolierten ihre Ergebnisse, Schätzung, dass ein Nationalstaat eine 1024-Bit-Primzahl brechen könnte. Das akademische Team unterbrach die am häufigsten verwendete 1024-Bit-Primzahl und schätzte, dass ein Gegner 18% der eine Million beliebtesten HTTPS-Websites überwachen könnte.

Sie fügten hinzu, dass ein zweiter Prime es dem Gegner ermöglichen würde, die Verbindungen von 66% der VPN-Server und 26% der SSH-Server zu entschlüsseln. Später in dem Bericht schlugen die Wissenschaftler vor, dass die NSA möglicherweise bereits über diese Fähigkeiten verfügt.

“Eine genaue Betrachtung der veröffentlichten NSA-Lecks zeigt, dass die Angriffe der Agentur auf VPNs mit einer solchen Unterbrechung vereinbar sind.”

Trotz dieser Sicherheitsanfälligkeit kann der Diffie-Hellman-Schlüsselaustausch weiterhin sicher sein, wenn er ordnungsgemäß implementiert wird. Solange ein 2048-Bit-Schlüssel verwendet wird, funktioniert der Logjam-Angriff nicht. Aktualisierte Browser sind ebenfalls vor diesem Angriff geschützt.

Ist der Diffie-Hellman-Schlüsselaustausch sicher??

Während der Diffie-Hellman-Schlüsselaustausch komplex erscheint, ist er ein wesentlicher Bestandteil des sicheren Datenaustauschs online. Solange es zusammen mit einer geeigneten Authentifizierungsmethode implementiert wird und die Nummern richtig ausgewählt wurden, gilt es nicht als anfällig für Angriffe.

Der Diffie-Hellman-Schlüsselaustausch war eine innovative Methode, mit der zwei unbekannte Parteien sicher kommunizieren konnten, als er in den 1970er Jahren entwickelt wurde. Während wir jetzt neuere Versionen mit größeren Schlüsseln implementieren, um vor moderner Technologie zu schützen Das Protokoll selbst scheint bis zum Eintreffen des Quantencomputers weiterhin sicher zu sein und die fortschrittlichen Angriffe, die damit einhergehen.

Cyber-Security-Business-Technologie von TheDigitalArtist lizenziert unter CC0