Was ist 3DES-Verschlüsselung und wie funktioniert DES?

3DES ist eine Verschlüsselungsverschlüsselung, die vom ursprünglichen Data Encryption Standard (DES) abgeleitet wurde. Es wurde in den späten Neunzigern bekannt, ist aber seitdem aufgrund der Zunahme sicherer Algorithmen in Ungnade gefallen.

Obwohl es im Jahr 2023 veraltet sein wird, wird es in einigen Situationen immer noch implementiert. Da es auf einem der ersten weit verbreiteten und untersuchten Algorithmen, DES, basiert, ist es immer noch wichtig zu lernen, was 3DES ist und wie es funktioniert.

In diesem Handbuch werden Sie ausführlich durch die einzelnen Schritte des DES-Prozesses geführt und anschließend erläutert, wie DES in 3DES geändert wird, um die Sicherheit zu erhöhen. Es werden auch die verschiedenen Sicherheitsprobleme angesprochen und ob Sie den Algorithmus verwenden sollten oder nicht.

Was ist 3DES??

Obwohl es offiziell als Triple Data Encryption Algorithm (3DEA) bekannt ist, wird es am häufigsten als 3DES bezeichnet. Dies liegt daran, dass der 3DES-Algorithmus die DES-Verschlüsselung (Data Encryption Standard) dreimal verwendet, um seine Daten zu verschlüsseln.

DES ist ein Symmetric-Key-Algorithmus, der auf einem Feistel-Netzwerk basiert. Als symmetrische Schlüsselverschlüsselung wird derselbe Schlüssel sowohl für die Verschlüsselung als auch für die Entschlüsselung verwendet. Das Feistel-Netzwerk macht diese beiden Prozesse nahezu identisch, was zu einem Algorithmus führt, dessen Implementierung effizienter ist.

DES hat sowohl eine 64-Bit-Block- als auch eine Schlüsselgröße, in der Praxis gewährt der Schlüssel jedoch nur 56-Bit-Sicherheit. 3DES wurde aufgrund der geringen Schlüssellänge von DES als sicherere Alternative entwickelt. In 3DES wird der DES-Algorithmus dreimal mit drei Schlüsseln ausgeführt. Er wird jedoch nur als sicher angesehen, wenn drei separate Schlüssel verwendet werden.

Die Verwendung von 3DES

Sobald die Schwächen des normalen DES erkennbar wurden, wurde 3DES in einer Vielzahl von Anwendungen eingesetzt. Es war eines der am häufigsten verwendeten Verschlüsselungsverfahren vor dem Aufkommen von AES.

Einige Beispiele für die Implementierung waren Microsoft Office, Firefox und EMV-Zahlungssysteme. Viele dieser Plattformen verwenden 3DES nicht mehr, weil es bessere Alternativen gibt.

Das Nationale Institut für Standards und Technologie (NIST) hat einen Entwurf eines Vorschlags veröffentlicht, der besagt, dass alle Formen von 3DES bis 2023 auslaufen und ab 2024 nicht mehr zugelassen werden. Obwohl es sich nur um einen Entwurf handelt, bedeutet der Vorschlag das Ende einer Ära, und es ist längst überholt, sich anderen, sichereren Algorithmen zuzuwenden.

Die Geschichte der 3DES-Verschlüsselung

Da 3DES von DES abgeleitet ist, ist es am besten, zuerst den früheren Standard einzuführen. In den siebziger Jahren suchte das National Bureau of Standards (NBS – inzwischen in NIST umbenannt) nach einem Algorithmus, der als Standard für die Verschlüsselung sensibler, aber nicht klassifizierter Regierungsinformationen verwendet werden kann.

Die NBS akzeptierte Vorschläge für einen Standard, der ihren Anforderungen entsprach, aber keiner der Kandidaten aus der ursprünglichen Runde war geeignet. Es wurden weitere Einsendungen eingeladen, und diesmal schickte IBM einen von seinem Team entwickelten Algorithmus durch. Die Vorlage wurde von der Luzifer-Chiffre abgeleitet, die Horst Feistel entworfen hat.

1975 wurde der IBM-Algorithmus von der NBS als vorgeschlagener Datenverschlüsselungsstandard veröffentlicht. Die Öffentlichkeit wurde gebeten, sich zu dem Entwurf zu äußern, der einige Kritik hervorrief.

Prominente Kryptografen wie Whitfield Diffie und Martin Hellman, Designer des Diffie-Hellman-Schlüsselaustauschs, behaupteten, die Schlüssellänge sei zu kurz und die S-Boxen seien von ihrem ursprünglichen Design abgeändert worden.

Zu der Zeit dachten viele in der kryptografischen Gemeinschaft, dass die NSA das Projekt sabotiert und den Algorithmus geschwächt hatte, so dass es die einzige Agentur sein würde, die DES brechen könnte.

Als dies vom US-Senatsausschuss für Geheimdienste untersucht wurde, stellte sich heraus, dass „die NSA IBM davon überzeugt hat, dass eine reduzierte Schlüsselgröße ausreicht; indirekt an der Entwicklung der S-Box-Strukturen beteiligt; und bestätigte, dass der endgültige DES-Algorithmus nach bestem Wissen frei von statistischen oder mathematischen Schwächen war. “

In demselben Bericht heißt es weiter, dass die „NSA in keiner Weise an dem Design manipuliert hat“. Dies wurde von einigen ehemaligen IBM-Mitarbeitern bestätigt, die behaupteten, der DES-Algorithmus sei vollständig vom IBM-Team entwickelt worden.

In der von der NSA freigegebenen Dokumentation heißt es, die Agentur habe “eng mit IBM zusammengearbeitet, um den Algorithmus gegen alle Angriffe mit Ausnahme von Brute-Force-Angriffen zu stärken und die Substitutionstabellen zu stärken …”

Der Verdacht auf NSA-Manipulation wurde in den neunziger Jahren gelindert, als die differenzielle Kryptoanalyse öffentlich entdeckt wurde. Als die häufig bösartigen S-Boxen mit der neuen Technik getestet wurden, erwiesen sie sich als angriffsresistenter als wenn sie zufällig ausgewählt worden wären.

Dies deutet darauf hin, dass das IBM-Team bereits in den siebziger Jahren von der differenziellen Kryptoanalyse wusste. Steven Levy behauptete, die NSA habe sie gebeten, die Technik geheim zu halten, um die nationale Sicherheit zu schützen.

Der berühmte Kryptograf Bruce Schneier sagte einmal: “Es hat zwei Jahrzehnte gedauert, bis die akademische Gemeinschaft herausgefunden hat, dass die” Optimierungen “der NSA tatsächlich die Sicherheit von DES verbessert haben.”

Trotz der anfänglichen Fragen zur Sicherheit des Algorithmus und zur Beteiligung der NSA wurde der IBM-Algorithmus 1976 als Datenverschlüsselungsstandard anerkannt. Er wurde 1977 veröffentlicht und 1983, 1988 und 1993 als Standard bestätigt.

Als die lineare Kryptoanalyse 1994 erstmals veröffentlicht wurde, stellten sich Fragen zur Sicherheit des Algorithmus. 1997 gab NIST bekannt, dass nach einem Algorithmus gesucht wird, der DES ersetzen soll. Die Notwendigkeit eines neuen Algorithmus wurde mit der Weiterentwicklung der Technologie und der Zunahme potenzieller Angriffe verstärkt.

Verschiedene Cracking-Versuche haben gezeigt, dass es weniger schwierig ist, den Algorithmus zu knacken, als bisher angenommen. Im Jahr 1998 war Distributed.net in der Lage, DES zu knacken ist 39 Tage.

Anfang 1999 hatte die Electronic Frontier Foundation mit Deep Crack die Zeit auf etwas mehr als 22 Stunden verkürzt. Dies signalisierte das Ende von DES, da ein Angriff dieser Art nun in Reichweite eines gut ausgestatteten Gegners lag.

Das Hauptproblem war der kleine Schlüsselraum, und ein neuer Algorithmus wurde dringend benötigt. Dies war ein Problem, da es mehrere Jahre dauern würde, bis sich NIST mit dem Algorithmus einverstanden erklärt, der zum Ersatzstandard, dem Advanced Encryption Standard (AES), wurde..

Während die Verschlüsselung für AES beschlossen wurde, wurde 3DES als Notlösung vorgeschlagen. Dabei wird der DES-Algorithmus dreimal mit drei separaten Schlüsseln ausgeführt. 1999 wurde DES erneut bestätigt, jedoch mit 3DES als idealem Algorithmus. Normales DES war nur in Legacy-Anwendungen zulässig.

3DES entwickelte sich zu einem weit verbreiteten Verschlüsselungsalgorithmus, der jedoch aufgrund seines hohen Ressourcenverbrauchs und seiner Sicherheitsbeschränkungen in den meisten Anwendungsfällen durch AES ersetzt wurde.

Verständnis des DES-Algorithmus

Bevor wir uns mit den Details von 3DES befassen können, ist es wichtig, den DES-Algorithmus zu verstehen, von dem er abgeleitet ist. Fangen wir also gleich am Anfang an.

Wir verwenden Verschlüsselung, um unsere Klartextdaten in Chiffretext umzuwandeln. Dies sind Informationen, auf die Angreifer nicht zugreifen können (solange wir geeignete Algorithmen verwenden)..

Verschlüsselungsalgorithmen sind im Wesentlichen komplexe mathematische Formeln. Wenn es darum geht, etwas wie “Lass uns zum Strand gehen” zu verschlüsseln, sind viele Leute verwirrt. Wie kann man Mathematik auf Dinge wie Buchstaben und Zeichen anwenden??

Kodierung des Textes

In Wirklichkeit handelt es sich bei Computern nicht um Buchstaben und Zeichen. Stattdessen arbeiten sie mit einem System von Einsen und Nullen, das als binär bezeichnet wird. Jede 1 oder 0 wird als Bit bezeichnet, und eine Sammlung von acht von ihnen wird als Byte bezeichnet.

Sie können entweder manuell nachschlagen oder einen Online-Konverter verwenden, um in der Binärdatei zu sehen, dass “Auf zum Strand” wie folgt lautet:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

Blöcke

Wenn Daten verschlüsselt sind, werden sie zur Verarbeitung in separate Blöcke unterteilt. DES hat eine 64-Bit-Blockgröße, was im Wesentlichen bedeutet, dass jeder Block einer Mischung aus 64 Einsen und Nullen entspricht. Unser erster Block (die ersten 64 Ziffern der oben gezeigten Binärdatei) wäre:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Unser zweiter wäre:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

Und unser letzter Block wäre:

01100010 01100101 01100001 01100011 01101000

Polsterung

Sie haben vielleicht bemerkt, dass unser dritter Block nur 40 Bit lang ist. Bevor es verschlüsselt werden kann, muss es auf eine 64-Bit-Blockgröße aufgebaut werden. Dies ist erledigt mit Polsterung, Dazu müssen Sie einem Block zusätzliche Informationen hinzufügen, um ihn zu vervollständigen. Dies kann mit einer Reihe von verschiedenen Schemata geschehen und dazu dienen, verschlüsselte Informationen schwieriger zu knacken, aber wir werden in diesem Artikel nicht darauf eingehen.

Der DES-Schlüsselplan

Verschlüsselungsalgorithmen verwenden Schlüssel, um Daten hinzuzufügen, die das Endergebnis des Prozesses verändern. Wenn DES nur Schritte wie Permutation und S-Boxen umfasste (die Permutation wird unten erklärt, während S-Boxen in der Tabelle behandelt werden Auswechslung Abschnitt), alles, was ein Angreifer tun müsste, ist die Details des Algorithmus aufzudecken, und dann jeden der Schritte in umgekehrter Reihenfolge auszuführen, um die ursprüngliche Nachricht zu enthüllen.

Da die meisten unserer Algorithmen allgemein bekannt sind, würde dies nicht wirklich zu mehr Sicherheit führen. Stattdessen werden geheime Schlüssel hinzugefügt, um die Ausgabe auf eine Weise zu ändern, die nicht durch Kenntnis des Algorithmus vorhergesagt werden kann (solange ein ausreichend komplexer Algorithmus verwendet wird)..

DES beginnt mit einem einzelnen Schlüssel, mit dem Unterschlüssel erstellt werden, die in jeder Runde angewendet werden. Dies ist ein 64-Bit-Schlüssel, der genauso groß ist wie unsere Blöcke. Angenommen, unser Schlüssel lautet:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Nun, diese Eingabe erfolgt in binärer Form. Dies ist die Art und Weise, wie Daten ausgedrückt werden, wenn Computer sie verarbeiten. Wenn Menschen mit Schlüsseln umgehen, erscheinen sie normalerweise als eine Mischung aus Zeichen, etwa so:

kj329nf982bc9wn1

In DES besteht der erste Schritt zum Ableiten unserer runden Schlüssel darin, den Schlüssel gemäß der folgenden Tabelle zu permutieren (zu verschieben):

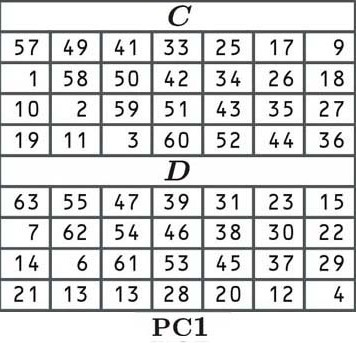
Bei der Permutation wird jedes Bit unseres Originalschlüssels an eine neue Position gemischt, wie in der Tabelle angegeben. Da steht die Zelle in der linken oberen Ecke (von C) 57, Die erste Nummer unseres permutierten Schlüssels ist die Nummer an der 57. Stelle unseres alten Blocks:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Die zweite Zelle sagt 49, Dies bedeutet, dass die zweite Ziffer unseres neuen Schlüssels die Nummer ist, die sich an der 49. Position unseres alten Blocks befindet:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Die dritte Zelle sagt 41, Also suchen wir nach der Ziffer an der 41. Position:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Bisher besteht unser Schlüssel aus110“.

Der Rest des Schlüssels ist entsprechend den Werten der Tabelle auf die gleiche Weise angeordnet. Wir bewegen uns von links nach rechts, und sobald wir am Ende einer Reihe angelangt sind, springen wir wie gewohnt zur nächsten hinunter. Einmal Tabelle C ist fertig, wir springen zu Tisch D die zweite Hälfte des Schlüssels zu vervollständigen.

Es gibt keine einfache Möglichkeit, unseren gesamten Block gemäß der anfänglichen Permutationstabelle zu transponieren. Sie könnten das Ganze manuell machen oder ein Skript dafür schreiben (oder sogar Glück haben und eines in den Tiefen des Internets finden), aber wir werden schummeln und es erfinden:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

Sie könnten besorgt sein, dass wir einige der Zahlen in diesem Handbuch zusammenstellen, aber die Realität ist, dass es nicht wirklich wichtig ist. Daten werden nicht mehr manuell verschlüsselt, sondern über Programme. Der wichtigste Aspekt dieses Tutorials ist, dass Sie eine klare Vorstellung von den Konzepten haben, mit denen wir uns befassen. Die Zahlen selbst dienen lediglich zur Veranschaulichung der Vorgänge.

Einige Leser haben vielleicht bemerkt, dass die Tabelle (und jetzt unser Schlüssel) nur 56 statt 64 Bits enthält. Dies liegt daran, dass jedes achte Bit übersprungen wird. Dies ist ein Artefakt aus früheren Zeiten der Technologie, als es wichtig war, Paritätsprüfbits zu haben, die überprüften, ob der Schlüssel korrekt empfangen wurde. Diese Paritätsprüfbits bedeuten, dass DES in der Praxis nur die Sicherheit eines 56-Bit-Schlüssels hat.

Die Tabellen C und D geben uns einen Schlüssel mit zwei 28-Bit-Hälften. Manchmal werden die Hälften als C und D bezeichnet, aber in diesem Artikel werden wir sie für links und rechts als L und R bezeichnen. Unsere linke Seite ist:

1100010 1010010 1010101 0101010

Während unser Recht ist:

1010000 1111001 0001011 1000111

Der nächste Schritt besteht darin, die Taste je nach Runde um ein oder zwei Leerzeichen nach links zu verschieben. Die genaue Anzahl der Plätze wird gemäß der folgenden vorgegebenen Tabelle festgelegt:

RundenzahlAnzahl der linken Schichten

1	1
2	1
3	2
4	2
5	2
6	2
7	2
8	2
9	1
10	2
11	2
12	2
13	2
14	2
15	2
16	1

Nehmen wir also die linke und rechte Hälfte:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

Und verschieben Sie beide um eine Position nach links, da die erste Runde eine Verschiebung von hat 1 laut tabelle (die nummer am linken ende wird an das rechte ende verschoben).

Erster runder Unterschlüssel:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

In der zweiten Runde steht auch auf dem Tisch 1, Daher wird dieses Ergebnis erneut geändert, indem jede Position um eine Stelle nach links verschoben wird.

Zweite Runde Unterschlüssel:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

In der dritten Runde werden die Zahlen um zwei Stellen nach links verschoben, weil in der Tabelle jetzt steht 2.

Unterschlüssel der dritten Runde:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

In den folgenden Runden werden die Zahlen entsprechend den in der Tabelle angegebenen Abständen nach links verschoben, wobei jede Verschiebung auf das Ergebnis der vorherigen Runde angewendet wird. Am Ende erhalten wir 16 verschiedene Unterschlüssel, einen für jede Runde des DES-Prozesses.

Der nächste Schritt ist eine andere Permutation gemäß der unten gezeigten PC2-Tabelle:

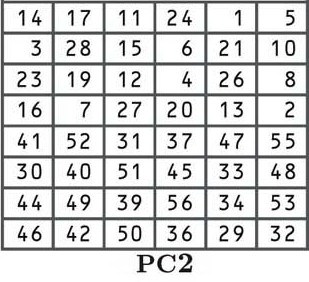
Inzwischen sollten Sie mit Permutationen vertraut sein, damit wir nicht weiter darauf eingehen. Wenn Sie mehr über die Funktionsweise erfahren möchten, lesen Sie die Erläuterungen am Anfang dieses Abschnitts. Obwohl die Umzugspositionen unterschiedlich sind, ist der Prozess der gleiche.

Jede der 16 im Schaltvorgang abgeleiteten Tasten wird nun gemäß der Tabelle gemischt, wobei die Nummer von der 14. Position auf die erste Stelle, die 17. auf die zweite, die 11. auf die dritte Position usw. Verschoben wird..

Wenn Sie sich die Tabelle genau ansehen, werden Sie feststellen, dass es nur 48 Bits statt der 56 Bits gibt, die wir zuvor hatten. Dieser Vorgang wird als Kompressionspermutation bezeichnet.

Sie können auch sehen, dass die obere Hälfte der Tabelle Nummern zwischen eins und 28 enthält, während die untere Hälfte Nummern zwischen 29 und 56 enthält. Dies hält die linke und rechte Hälfte unserer Unterschlüssel getrennt und wird unten durch das größere Leerzeichen angezeigt in der Mitte der Tasten.

Wieder werden wir schummeln und die Zahlen erfinden. Nehmen wir an, dieser gesamte Prozess hat uns die folgenden Unterschlüssel gegeben:

Runde eins:         010101 010101 101010 110100 101001 100101 101010 101010

Runde Zwei:         011010 110101 101110 110010 010100 110010 111101 101101

Runde drei:     010100 100110 110110 101010 100110 011000 101011 011001

Runde vier:         011001 110101 011001 110101 000011 001011 010101 010101

Runde fünf:         110101 001101 010101 010101 010011 001011 010111 100101

Runde sechs:           010111 110101 011001 111001 101001 100101 101010 101010

Runde sieben:     110101 111010 101110 101010 100110 010110 111011 001110

Achtelfinale:       011001 110101 010101 001001 010011 001011 010100 101010

Neunte runde:         111011 011010 011110 100010 100010 010110 110011 110010

Runde 10:             011010 010101 101110 101001 010010 010110 111000 101010

Runde 11:             110101 001101 101110 101010 100101 100101 101010 001010

Runde 12:             101001 100100 101001 101010 100110 011000 101011 011001

Runde 13:             010010 010010 010101 010101 010110 110001 100101 101010

Runde 14:             101001 100110 010101 011101 010001 001010 110010 111110

Runde 15:             011001 011010 011001 110101 001001 011001 100101 101101

Runde 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Dieser Verschiebungsprozess führt dazu, dass jedes Bit des Anfangsschlüssels in ungefähr 14 der 16 Unterschlüssel verwendet wird, obwohl einige Bits etwas häufiger als andere verwendet werden.

Anfangspermutation

Nachdem die Daten in Blöcke unterteilt und bei Bedarf aufgefüllt wurden, kann der DES-Verschlüsselungsprozess gestartet werden. Wir werden zu den Unterschlüsseln zurückkehren, die wir zu einem späteren Zeitpunkt erstellt haben. Der erste Schritt wird als anfängliche Permutation bezeichnet, bei der die Daten gemäß der folgenden Tabelle neu angeordnet werden:

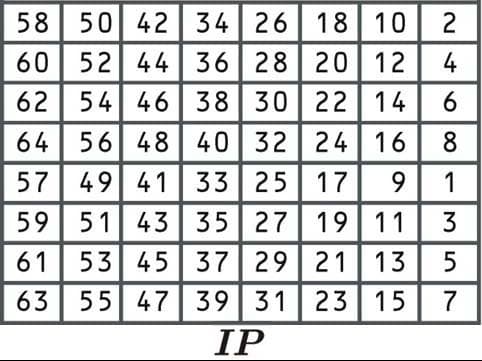
Dieser anfängliche Permutationsprozess macht den Algorithmus nicht sicherer. Dies liegt daran, dass die Eingabe von Schlüsseln nicht erforderlich ist und einfach rückgängig gemacht werden kann. Der Algorithmus wurde ursprünglich auf diese Weise entwickelt, da er die Implementierung in bestimmten Kontexten erleichtert.

Da wir einige Male auf Permutationen eingegangen sind, werden wir hier keine wesentlichen Erklärungen auslassen. Geh zurück zu Der DES-Schlüsselplan Abschnitt, wenn Sie weitere Informationen zur Funktionsweise benötigen.

Nehmen wir den ersten Block von der Meldung “Lass uns zum Strand gehen”, die wir in der Block Abschnitt unter Verständnis des DES-Algorithmus:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Da sagt die erste Zelle 58, Wir würden die Nummer von der 58. Position wählen:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Dann würden wir die Nummer von der 50. Position nehmen:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Und die Nummer von der 42. Position:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Das gibt uns “110” bisher. Wir werden den Rest der Nummer machen:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Wenn die anfängliche Permutation abgeschlossen ist, werden die Daten zum nächsten Schritt weitergeleitet.

Teile die Blöcke auf

Sobald die Daten ihre anfängliche Permutation durchlaufen haben, werden sie in zwei Hälften geteilt. Wir nehmen unseren Block, der gerade seine anfängliche Permutation durchgemacht hat:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Und wir werden es in zwei Blöcke aufteilen, einen linken Block (bestehend aus den ersten 32 Ziffern), bekannt als L0:

L0    11010111 01001010 10101000 10011101

Und ein rechter Block (bestehend aus den zweiten 32 Ziffern), bekannt als R0:

R0    01001011 10110101 10000111 10101001

Die F-Funktion

Nachdem der Block aufgeteilt wurde, ist es Zeit für die F-Funktion. In der ersten Runde wird es nur auf die rechte Hälfte des Blocks angewendet, während die linke Hälfte bis später beiseite bleibt. Die rechte Seite durchläuft die folgenden vier Schritte als Teil der F-Funktion:

• Expansionspermutation (E im Diagramm)
• Tastenmischung (⊕ im Diagramm)
• Substitution (jeweils S1, S2 etc. im Diagramm)
• Permutation (P im Diagramm)

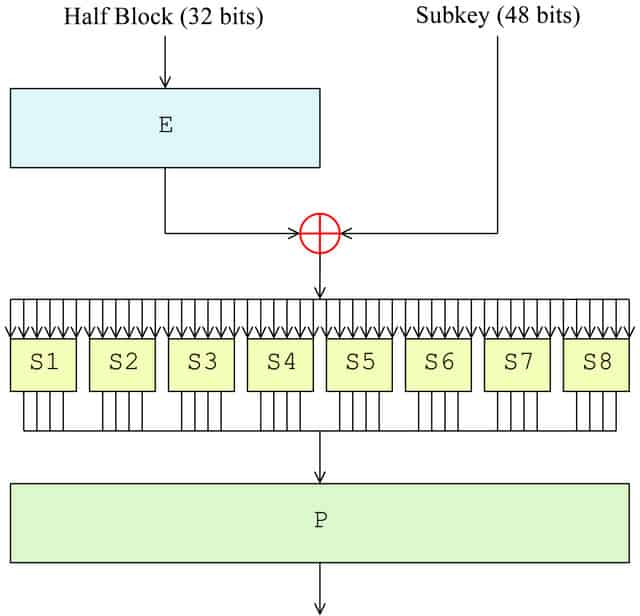
Expansionspermutation

Die Expansionspermutation bewirkt drei Dinge. Das Wichtigste ist, dass einzelne Bits von Eingabedaten die Ausgabe von zwei anderen Bits beeinflussen und einen Lawineneffekt verursachen. Es macht auch die rechte Hälfte 48-Bit, so dass es die gleiche Größe wie der Unterschlüssel für den nächsten Schritt ist. Der andere Effekt der Expansionspermutation besteht darin, dass die Ausgabe länger als die Eingabe ist. Dadurch kann es im Ersetzungsvorgang komprimiert werden.

Die Bits sind gemäß der folgenden Tabelle neu angeordnet. Einige der einzelnen Bits befinden sich zweimal in der Tabelle. So wurde der Block von 32 auf 48 Bits erweitert:

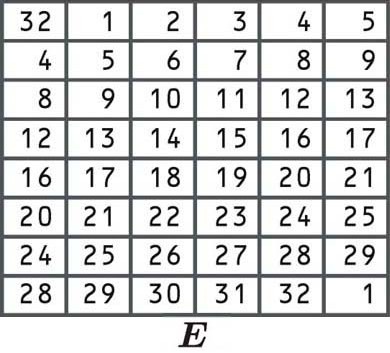
Da in der ersten Zelle 32 steht, nehmen wir unseren rechten Block und wählen die Nummer von der 32. Position aus, genau wie wir es in den anderen oben aufgeführten Permutationsbeispielen getan haben:

R0    01001011 10110101 10000111 10101001

Wir nehmen dann die Zahlen von der ersten Position, der zweiten Position und so weiter, bis wir zur unteren rechten Ecke des Blocks gelangen. Da gibt es eine 1 In dieser Zelle ist die letzte Ziffer auch die Nummer, die an der ersten Stelle unseres Blocks steht.

Nehmen wir an, die Erweiterungspermutation liefert einen neuen 48-Bit-Block mit:

101110 100110 100100 000000 001100 001110 101101 011110

Key mischen

Nachdem der Block auf 48 Bit erweitert wurde, ist es an der Zeit, den Unterschlüssel der ersten Runde anzuwenden, den wir in der Tabelle abgeleitet haben DES Schlüsselplan Abschnitt oben. Der Block wird vom Unterschlüssel mit der XOR-Chiffre geändert.

Die XOR-Verschlüsselung ist eine Additionsverschlüsselung, die einem einfachen Prozess folgt, insbesondere im Vergleich zu den anderen Elementen, die wir bereits besprochen haben.

In einer XOR-Chiffre:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Nehmen wir also an, Sie müssen die folgenden beiden Zahlen binär XOR-verknüpft haben:

1101

0101

Jede Ziffer würde zu der darunter liegenden Ziffer hinzugefügt. Nach den drei oben gezeigten Regeln ergibt sich folgendes Ergebnis:

1000

Um den Schlüsselmischungsschritt abzuschließen, nehmen wir die rechte Seite unseres Blocks, die wir gerade auf 48 Bits erweitert haben, und den ersten runden Schlüssel. Wir führen dann die XOR-Addition durch:

Block:                      101110 100110 100100 000000 001100 001110 101101 011110

Runder Schlüssel:     010101 010101 101010 110100 101001 100101 101010 101010

XOR-Ergebnis:             111011 110011 001110 110100 100101 101011 000111 110100

Das Ergebnis der XOR-Operation wird dann an die nächste Runde weitergereicht.

Auswechslung

Substitution fügt Datenverwirrung hinzu. Dies geschieht normalerweise mit Nachschlagetabellen, die auch als Substitutionsfelder oder S-Felder bezeichnet werden. DES verwendet acht separate Tabellen oder S-Boxen, eine andere für jeweils 6 Datenbits. Die folgende Tabelle zeigt die acht S-Boxen von DES:

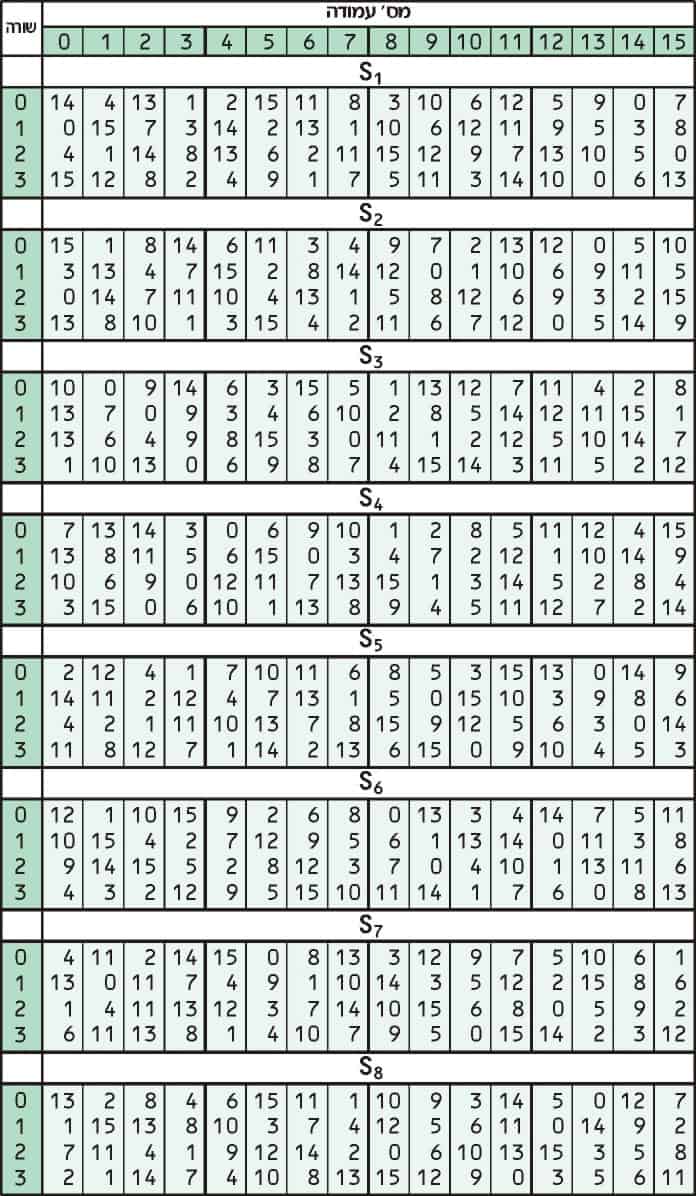
Die acht separaten S-Boxen werden verwendet, um jeden 6-Bit-Eingang in einen 4-Bit-Ausgang zu übersetzen. Der erste Schritt besteht darin, die Ziffern am Anfang und Ende eines 6-Bit-Segments zu nehmen und diesen Binärwert in eine Dezimalzahl umzuwandeln.

Nehmen wir die Daten, die wir gerade im vorherigen Schritt mit XOR beendet haben:

111011 110011 001110 110100 100101 101011 000111 110100

Wir werden uns das erste 6-Bit-Segment ansehen, um Ihnen zu zeigen, wie der Substitutionsprozess funktioniert:

111011

Da sind die erste Nummer und die letzte Nummer beide 1, das gibt uns einen Wert von 11. Wir konvertieren dann 11 von binär zu dezimal, was uns gibt 3. Dies sind nur äquivalente Werte, die unterschiedlich geschrieben sind. Stellen Sie sich vor, Sie wandeln die Computersprache in die menschliche Sprache um. Sie können die Konvertierung mit einem Online-Rechner selbst überprüfen, wenn Sie möchten.

Wir nehmen dann die vier mittleren Ziffern des ersten 6-Bit-Segments:

111011

Und konvertieren Sie sie von binär nach dezimal. 1101 übersetzt zu Nummer 13.

Nun nehmen wir diese beiden Zahlen und schlagen sie im nach S1 Tabelle:

               

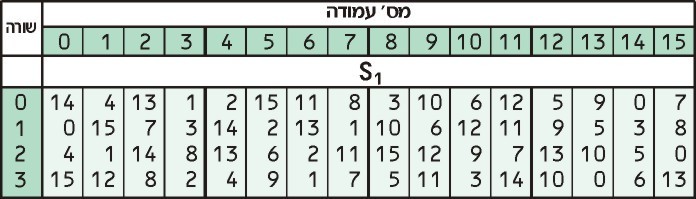
Unsere erste Nummer, 3, sagt uns, dass wir in die dritte Reihe schauen sollen, während unsere zweite Nummer, 13 sagt uns, in die 13. Spalte zu schauen. Der Wert in der dritten Zeile der 13. Spalte ist 0.

Nachdem wir unsere Nummer in der Tabelle nachgeschlagen haben, konvertieren wir sie zurück in eine vierstellige Binärzahl. Null wird normalerweise als 0 in binär geschrieben, aber 0000 ist das gleiche, und dies ist das Format, das für unsere Zwecke am besten geeignet ist.

Nach diesem Vorgang konvertiert die S-Box unseren ersten 6-Bit-Datenabschnitt (111011) in einen anderen 4-Bit-Wert (0000). Es scheint verwickelt zu sein, aber diese Technik hilft, die Beziehung zwischen dem Chiffretext und dem Klartext, mit dem er verknüpft ist, weiter zu verschleiern.

Der nächste 6-Bit-Datenabschnitt durchläuft dann denselben Prozess, verwendet jedoch stattdessen die oben gezeigte S2-Box. Der dritte Abschnitt verwendet die S3-Tabelle usw., bis der letzte Abschnitt durch die S8-Tabelle ersetzt wird.

Wieder werden wir den Rest der Werte betrügen. Nehmen wir an, dass die Substitutionsfelder folgende Ergebnisse liefern:

0000 1010 1100 1001 0100 1001 0111 0001

Sobald jeder Abschnitt der Daten seine S-Box durchlaufen hat, wird mit dem nächsten Schritt fortgefahren.

Permutation

Die letzte Stufe der F-Funktion ist eine andere Permutation unter Verwendung der folgenden Tabelle: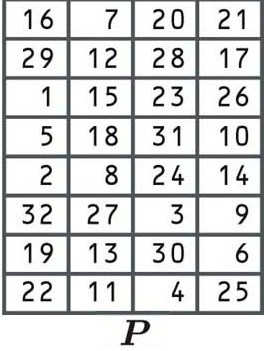

Inzwischen sollten Sie ein gutes Verständnis dafür haben, wie Permutationen Ziffern vom alten Block an eine andere Position im neuen Block verschieben, damit wir nicht noch einmal darauf eingehen.

Nehmen wir an, diese Permutation entspricht unserem vorherigen Ergebnis:

0000 1010 1100 1001 0100 1001 0111 0001

Und gibt uns eine Ausgabe von:

0101 0110 1001 0101 0010 0100 0101 0010

Nachdem die Permutation abgeschlossen ist, haben wir die vier Schritte der F-Funktion in dieser Runde beendet. In der mathematischen Notation ist dieser Wert als bekannt f (R0, K1). Dies bedeutet, dass das Ergebnis die Funktion ist (f) der ersten rechten Seite des Blocks (R0) und des Unterschlüssels der ersten Runde (K1).

XOR mit dem linken Block

Erinnern Sie sich, wie wir den Block kurz vor Beginn der Schritte der F-Funktion in zwei Hälften geteilt haben? Wir legen die linke Seite des Blocks (L0) beiseite, während die rechte Seite jeden dieser Prozesse durchlief. Nun ist es an der Zeit, dass L0 wieder in Aktion tritt.

Wir nehmen die rechte Seite, die wir gerade bearbeitet haben f (R0, K1) und füge es der alten linken Seite hinzu (L0) mit der XOR-Chiffre. Das gibt uns R1, Das Ergebnis unserer ersten Runde:

f (R0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0:                                    1101 0111 0100 1010 1010 1000 1001 1101

XOR – Ergebnis (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Siehe die Key mischen Abschnitt oben, wenn Sie eine Erinnerung an die Funktionsweise der XOR-Verschlüsselung benötigen.

15 weitere Runden…

Wenn Sie so weit gekommen sind, scheint DES ein mühsamer Prozess zu sein. Aber es ist noch lange nicht fertig. Die Daten durchlaufen die vier Schritte der F-Funktion, gefolgt von einem weiteren 15-maligen XOR, was insgesamt 16 Runden ergibt.

In der zweiten Runde nehmen wir die ursprüngliche, unberührte Version der rechten Seite des Blocks (R0) und machen sie zur neuen linken Seite (L1). In der Zwischenzeit nehmen wir das Ergebnis unserer ersten Runde und senden es durch die F-Funktion. Alles geschieht wie beim letzten Mal, jedoch wird stattdessen der Unterschlüssel für Runde zwei verwendet. Nehmen wir an, dieser Prozess führt zu folgenden Ergebnissen:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Wir XOREN dann das Ergebnis mit L1, das eigentlich R0 ist (wir haben dies in der Formel 1 abgeleitet) Blöcke teilen Sektion). Dies gibt uns das Ergebnis der zweiten Runde, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Dieser Schritt kann etwas verwirrend wirken, aber nach dem Feistel-Schema wird die alte rechte Seite zur neuen linken, während das Ergebnis der Operation zur neuen rechten Seite wird.

Das folgende Diagramm gibt Ihnen eine visuelle Darstellung des Geschehens. IP stellt die anfängliche Permutation dar, F ist ein Ersatz für die gesamte F-Funktion, das ⊕ symbolisiert die XOR-Funktion und die Pfeile kennzeichnen jede Seite des Blocks, die sich zwischen links und rechts bewegt:

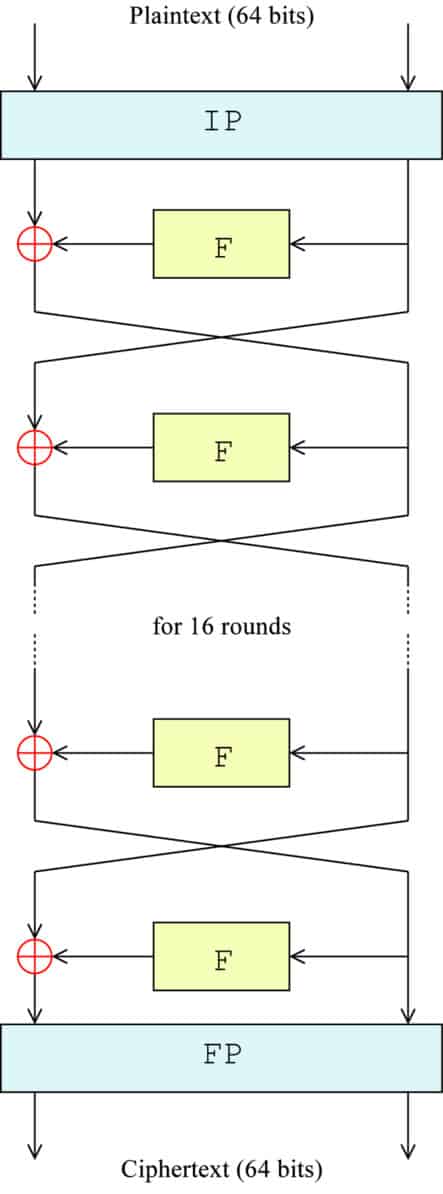
Die genaue Formel für jeden Schritt lautet:

Ln = Rn-1

Rn = Ln-1 + f(Rn-1,Kn)

Wo:

L = Die linke Hälfte des Blocks (beginnend mit L0, als der Block anfänglich geteilt wurde)

R = Die rechte Hälfte des Blocks (beginnend mit R0, als der Block anfänglich geteilt wurde)

n = Die runde Zahl (beginnend mit 0, als der Block anfänglich geteilt wurde)

f = Die F-Funktion

Kn = Der Unterschlüssel für Runde n

Gemäß der Formel und dem Diagramm wird R1 in der dritten Runde zur neuen linken Hälfte (L2), während R2 durch die F-Funktion verarbeitet wird. Nehmen wir an, wir erhalten ein Ergebnis von:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Wir berechnen dann das Ergebnis unserer dritten Runde (R3) mit der XOR-Chiffre wie zuvor:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

Der gleiche Vorgang wird bis zur fünfzehnten Runde fortgesetzt, wobei die Blöcke umgeschaltet werden und der nächste Unterschlüssel in jeder Runde verwendet wird. In der 16. und letzten Runde werden die Blöcke nicht umgeschaltet. Stattdessen werden sie zu einem 64-Bit-Block zusammengefasst. Wenn Sie in dieser letzten Phase auf das Vertauschen der Blöcke verzichten, kann der Algorithmus sowohl für die Verschlüsselung als auch für die Entschlüsselung verwendet werden.

Nehmen wir an, die Endrunde ergibt folgendes Ergebnis:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Endgültige Permutation

Diese Permutation ist die Umkehrung der anfänglichen Permutation und fügt wiederum keinen zusätzlichen Sicherheitswert hinzu. Es ordnet die Daten gemäß der folgenden Tabelle neu:

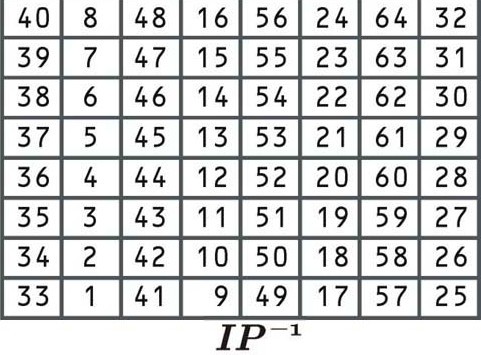
Diese Permutationstabelle funktioniert genauso wie die vorherigen. Da dies der letzte Schritt des Verschlüsselungsprozesses ist, ist das Ergebnis der Chiffretext für den ersten Block vonLass uns gehen zum Strand”. Nehmen wir an, der verschlüsselte Block ist:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Wenn Sie nun den echten Geheimtext für “Auf geht’s zum Strand” wollten, hätten Sie einfach den gesamten Lernprozess überspringen und direkt zu einem Online-DES-Verschlüsselungstool wechseln können. Wenn wir unseren Satz neben einem Schlüssel eingeben (sagen wir kj329nf982bc9wn1), erhalten wir einen verschlüsselten Text von:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Wenn Sie möchten, können Sie dann den Schlüssel und den Chiffretext in Binär umwandeln und dann vergleichen, wie der Chiffretext des ersten Blocks stimmt mit dem gesamten beschriebenen Prozess überein.

DES-Entschlüsselung

In DES ist der Entschlüsselungsprozess unglaublich einfach. Die Feistel-Struktur des Algorithmus ermöglicht eine einfache Umkehrung. Der Prozess läuft fast genauso ab, um Informationen zu entschlüsseln. Der einzige Unterschied besteht darin, dass die Unterschlüssel in umgekehrter Reihenfolge angewendet werden. Dies ist eine effiziente Einrichtung, da bei der Ver- und Entschlüsselung dieselbe Software und Hardware verwendet werden kann.

Um die Daten zu entschlüsseln, durchläuft sie zuerst eine anfängliche Permutation, dann wird der Block geteilt und die rechte Hälfte durchläuft die F-Funktion. Der Unterschied besteht darin, dass in der ersten Entschlüsselungsrunde der 16. Unterschlüssel angewendet wird. Alles andere läuft wie gewohnt ab. Sobald die F-Funktion abgeschlossen ist, wird sie mit der linken Seite des Blocks XOR-verknüpft.

Die Blöcke werden umgeschaltet und das Ergebnis durchläuft den gleichen Vorgang für die zweite Runde, mit der einzigen Ausnahme, dass der 15. Unterschlüssel angewendet wird. Dieser Vorgang wird bis zur 16. Runde fortgesetzt, wenn der 1. Unterschlüssel verwendet wird.

Genau wie beim Verschlüsselungsprozess werden die Blöcke in der letzten Phase nicht ausgetauscht, und dann werden die Daten einer endgültigen Permutation unterzogen. Damit ist der Entschlüsselungsvorgang abgeschlossen, und es wird der ursprüngliche Klartext der Nachricht angezeigt.

3DES

Als die Sicherheitsschwächen von DES immer deutlicher wurden, wurde 3DES als Methode zur Erweiterung der Schlüsselgröße vorgeschlagen, ohne einen völlig neuen Algorithmus erstellen zu müssen. Anstatt einen einzelnen Schlüssel wie in DES zu verwenden, führt 3DES den DES-Algorithmus dreimal mit drei 56-Bit-Schlüsseln aus:

• Schlüssel ist man gewohnt Verschlüsseln der Klartext.
• Taste zwei ist gewohnt entschlüsseln Der Text, der mit dem ersten Schlüssel verschlüsselt wurde.
• Taste drei ist es gewohnt Verschlüsseln der Text, der mit Schlüssel drei entschlüsselt wurde.

In jeder Phase wird der gesamte DES-Prozess wie oben beschrieben durchgeführt.

Jetzt wundern Sie sich vielleicht: “Wie kann das Anwenden der Entschlüsselung im zweiten Schritt die Sicherheit verbessern?”

Die Antwort ist, dass es einen separaten Schlüssel verwendet. Wenn der erste Schlüssel auch zum Entschlüsseln der Daten im zweiten Schritt verwendet wurde, befinden sich die Daten wieder genau dort, wo sie begonnen haben.

Da jedoch ein anderer Schlüssel verwendet wird, dient der Entschlüsselungsvorgang nicht zur eigentlichen Entschlüsselung der Daten. Es mag logisch pervers erscheinen, aber das Entschlüsseln mit einem separaten Schlüssel dient nur dazu, die Daten noch weiter durcheinander zu bringen.

Sobald der zweite Schlüssel die Daten “entschlüsselt” hat, wird der dritte Schlüssel angewendet, um sie erneut zu verschlüsseln. Das Ergebnis ist der 3DES-Chiffretext.

3DES ist auf diese Weise strukturiert, da Implementierungen mit DES mit einem Schlüssel, DES mit zwei Schlüsseln und DES mit drei Schlüsseln kompatibel sind (diese werden im folgenden Abschnitt behandelt). Dies würde nicht funktionieren, wenn die Verschlüsselung in allen drei Schritten verwendet würde.

3DES-Keying-Optionen

Technisch kann 3DES mit drei verschiedenen Schlüsselkonfigurationen implementiert werden. Trotzdem sind die zweite und dritte Option unsicher und sollten niemals implementiert werden.

• Eingabemöglichkeit eins – Diese Option verwendet drei unabhängige Schlüssel und ist am sichersten.
• Codierungsoption zwei – In dieser Konfiguration sind der erste und der dritte Schlüssel identisch.
• Codierungsoption drei – Dies verwendet drei identische Schlüssel. Wenn identische Schlüssel verwendet werden, hebt der Entschlüsselungsprozess in der zweiten Stufe die erste Verschlüsselung auf und lässt nur die endgültige Verschlüsselung übrig, um die Daten zu ändern. Dies macht das Ergebnis zum wie gewöhnliches DES.

Der 3DES-Prozess: Eingabe der ersten Option

Um ehrlich zu sein, der gesamte 3DES-Prozess kann Ihnen den Kopf verdrehen, insbesondere, wenn Sie mit Kryptografie noch nicht vertraut sind. Im Folgenden finden Sie eine kurze Zusammenfassung des gesamten Verschlüsselungsschemas des 3DES-Algorithmus:

Der Klartext wird in den 3DES-Algorithmus eingegeben und steht an erster Stelle verschlüsselt mit Schlüssel eins in den folgenden Schritten:

• • Schlüsselplan – Die 16 Unterschlüssel werden von Schlüssel 1 abgeleitet

  • Anfangspermutation

  • Der Block ist in eine linke und eine rechte Hälfte aufgeteilt

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die Runde

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Machen Sie die alte rechte Seite zur neuen linken Seite und das Ergebnis zur neuen rechten Seite

      Wiederholen Sie die obigen Schritte 14 Mal

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die 16. Runde

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Kombinieren Sie die linke und rechte Seite des Blocks

• • Endgültige Permutation

Nehmen Sie den mit Schlüssel 1 verschlüsselten Text und senden Sie ihn über die “Entschlüsselungs” -Prozess mit Schlüssel zwei:

• • Schlüsselplan – Die 16 Unterschlüssel werden von Schlüssel zwei abgeleitet

  • Anfangspermutation

  • Der Block ist in eine linke und eine rechte Hälfte aufgeteilt

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die Runde (ab dem 16. Unterschlüssel für die Entschlüsselung)

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Machen Sie die alte rechte Seite zur neuen linken Seite und das Ergebnis zur neuen rechten Seite

      Wiederholen Sie die obigen Schritte 14 Mal

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die erste Runde

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Kombinieren Sie die linke und rechte Seite des Blocks
  • Endgültige Permutation

Nehmen Sie die mit Schlüssel 2 “entschlüsselten” Daten und senden Sie sie über das enVerschlüsselungsprozess mit Schlüssel drei:

• • Schlüsselplan – Die 16 Unterschlüssel werden von Schlüssel drei abgeleitet

  • Anfangspermutation

  • Der Block ist in eine linke und eine rechte Hälfte aufgeteilt

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die Runde

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Machen Sie die alte rechte Seite zur neuen linken Seite und das Ergebnis zur neuen rechten Seite

      Wiederholen Sie die obigen Schritte 14 Mal

• • • Die rechte Hälfte wird über die F-Funktion gesendet

      • Expansionspermutation

      • XOR mit dem Unterschlüssel für die 16. Runde

      • Auswechslung

      • Permutation

    • XOR das Ergebnis der F-Funktion mit der linken Seite

    • Kombinieren Sie die linke und rechte Seite des Blocks

• • Endgültige Permutation

Das Ergebnis ist der 3DES-Chiffretext.

Die Sicherheit von 3DES

Die Sicherheit von 3DES hängt davon ab, welche Keying-Option verwendet wird. Bei der ersten Verschlüsselungsoption handelt es sich um drei verschiedene 56-Bit-Schlüssel, was einer Gesamtschlüssellänge von 168 Bit entspricht. Die effektive Länge wird durch Meet-in-the-Middle-Angriffe erheblich verringert, wodurch die reale Sicherheit auf 112 Bit reduziert wird.

Meet-in-the-Middle-Angriffe eignen sich für Verschlüsselungsverfahren, bei denen derselbe Algorithmus mehrmals wiederholt wird. Die Technik speichert die unmittelbaren Werte aus jeder Verschlüsselungsstufe und verwendet diese Informationen dann, um die Zeit, die erforderlich wäre, um den Algorithmus brachial zu erzwingen, radikal zu verbessern.

Die Optionen zwei und drei haben erheblich kleinere Schlüssel und sind sowohl für bekannte Klartext- als auch für ausgewählte Klartextangriffe sowie für andere anfällig.

Bekannte Klartext-Angriffe sind möglich, wenn ein Gegner sowohl auf den Klartext als auch auf den Chiffretext einer Nachricht zugreifen kann. Wenn ein Algorithmus für diese Angriffe anfällig ist, kann der Angreifer anhand dieser Informationen den Schlüssel ableiten, um alle anderen Daten zu knacken, die mit demselben Schlüssel verschlüsselt wurden.

Ein gewählter Klartext-Angriff ist ähnlich, aber der Angreifer entdeckt den Schlüssel, indem er Chiffretexte mit beliebigen Klartexten vergleicht.

Aufgrund dieser Sicherheitsanfälligkeiten und der insgesamt kleinen Schlüsselgrößen sind die Schlüsseloptionen zwei und drei unsicher und sollten nicht implementiert werden.

Ist 3DES sicher??

Da 3DES in den nächsten Jahren veraltet sein wird, ist es am besten, andere Algorithmen zu verwenden. Während die Verschlüsselungsoption 1 für viele Anwendungen immer noch als sicher gilt, gibt es nicht viele gute Gründe, warum sie anstelle einer Alternative wie AES verwendet werden sollte.

Obwohl 3DES als Nachfolger von DES einen wichtigen Platz in der Kryptografie einnimmt, sind seine glorreichen Jahre vorbei und es ist an der Zeit, weiterzumachen. Wenn Sie Ihre Systeme bis in die Zukunft sichern möchten, sollten Sie stattdessen einen aktuelleren Algorithmus verwenden.

Verbunden: Allgemeine Verschlüsselungsarten erklärt

Planen Sie X von DoD lizenziert unter CC0